.NetCore下B/S结构 初探基于遗传学算法的中学自动排课走班（一）

介绍：

实现本系统需要考虑的NP问题，本系统先针对中学（高、初、小）基本教室可以确定，所以可以暂时排除这个因素

先阐述下系统问题：

1、老师自定义条件（每个老师自定义设置）

2、课程的分布均匀度

3、课程的重要程度

4、课程上课效果程度

5、同一个老师同一时间只能上一门课

6、同一班级同一时间只能上一门课

7、在考虑教室的情况下（同一教室同一时间被一个班级使用同时上课班级的人数要小于教室容纳的人数）

 

其中 5、6、7是硬性条件限制 必须要满足，1、2、3、4 为软要求 尽量满足

针对这样的复杂问题怎么来求解并且要得到最优解（接近最优解）

本文主要还是用遗传学算法的方式来做设计（算法结合相应的.NetCore代码实现）

遗传学的概念理论知识可以百度研究，但是要理解是种群、种群个数、个体这个概率

 设计要合理，看了一些排课设计（他们把2个课时看成一个大课、一天分5个课时、一周5天 其实这样不是很合理）

记得我上高中那会 高三是放月假，一周只休息半天  每个年级都不一样  如果是小学可能没有晚自习 初高中都有晚自习 而且年级之前课时数还不一样

如现在上午有的学校是5节课 而有写学校是4节课，那么针对这样一个情况我们怎么来设计这个系统呢？

为了方便说下面2张图是我设计的案例（图中是事例不做参考）（目前是6个老师上2个班级6门课的教学计划）以上午5节课下午4节课为模版设计，而往往一个学校教师、班级都是比较多，后面我们将以100个班级150个老师9门课程来做测试分析，教学任务也相对复杂化，限制条件可能会比较多

 

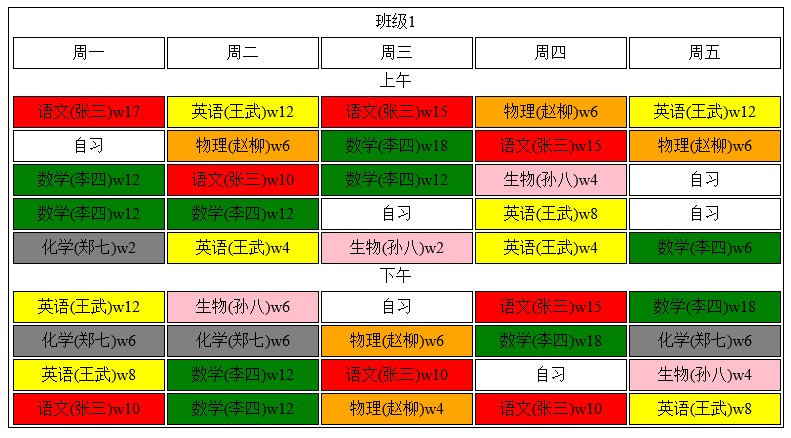
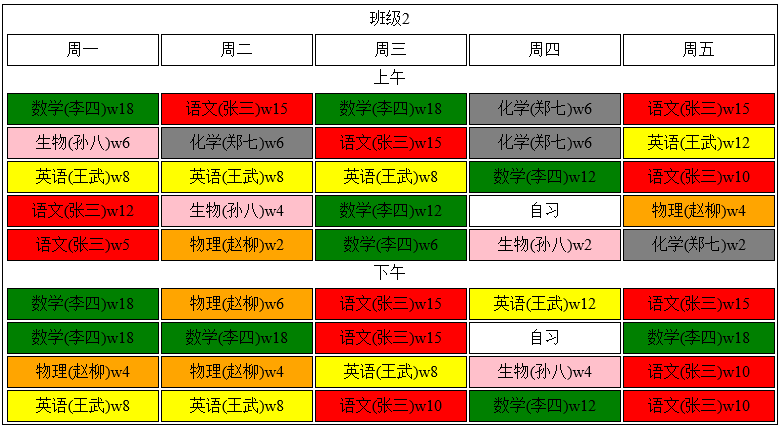
这里就代表我初始化了2个种群，而每个种群的个体数量为39、43

在系统设计过程中 要设计好评价函数、以及遗传算子（评价函数影响遗传算法收敛速度），常见的遗传算子有 轮盘赌博、交叉、变异

通过这些运算来实现最终结果（这个结果理论上接近最优解） 但是还有考虑其他问题 采用退火法防止出现局部最优解、以及TSP问题、还有就是对遗传算法的优化（精英、插入）操作，总之还是非常复杂

退火法：举个例子比如我们去爬山，要爬到最高的山峰上，但是有很多山峰，当我们爬到其中一座山山顶就以为这是最高位置（有人说人可以看啊），对程序也可以看，这就要提到退火法了，在遗传算法演变的N个子代中，这里可以把N个子代看作N座山峰，每个子代都有一个最高峰 ，如 某一个个体在 X1代中最高峰是 20米 但是在 X2......Xn中可能还存在比20高的位置，这就是退火法实现需要找出所有山峰中最高的点位

接下来的文章会加入源码来实现这个问题，（这个系列更新可能很慢，时间不够）看下最终是什么效果~