行列式

行列式

定义

对于方阵 \(A\)（方阵，即正方形的矩阵），用 \(\det(A)\) 或者 \(|A|\) 表示其行列式。

\[\det(A) = \sum_{\sigma \in S_n} (-1)^{sgn(\sigma)} \prod_{i=1}^n a_{i,\sigma_i} \]

其中 \(\sigma\) 表示一个长度为 \(n\) 的排列序列。\(sgn(\sigma)\) 表示排列 \(\sigma\) 的逆序对个数。

计算行列式

肯定不能直接算啦。

对行列式进行一些变换，使其变成只有右上三角有值的方阵。然后你发现，对这样一个方阵求行列式，只有 \(\sigma = \{1,2,\cdots , n\}\) 的时候，连乘才非零。因此只需要考虑这种情况。

但是如何变换呢？

行列式性质

1. 行列式与它的转置行列式相等，\(\det(D) = \det(D^T)\)。

   转置行列式是指，原行列式的第 \(i\) 行变成转置行列式的第 \(i\) 列，即 \(D_{i,j} = D^T_{j,i}\)。

   不难感觉到方阵的行列式的计算中，行和列本质是一样的。因此下面所有对行成立的性质，对列也成立。

2. 交换行列式的任意不同两行，行列式变号。

   引理：交换排列任意两个不同的数，排列逆序对个数奇偶性取反。

   交换两个相邻的数，显然成立。交换两个不相邻的数，可以看做进行若干次相邻交换操作，容易发现交换次数总是奇数，因此成立。

   交换行列式任意不同两行，我们连同其对应的排列 \(\sigma\) 一起换了，那么对于所有 \(\sigma \in S_n\)，\(sgn(\sigma)\) 奇偶性取反，所以行列式符号取反。

   推论 2-1：有两行一样的方阵，其行列式值为零。

   因为你交换这两行，行列式值取反，但是方阵没变，因此行列式值不变。所有行列式值为 \(0\)。

3. 行列式某一行每一个数同乘 \(k\)，行列式值乘上 \(k\)。

   显然吧，因为行列式计算的时候连乘那里恰好是每一行选一个数。

4. 行列式中如果有两行元素成比例，则此行列式为零。

   推论 2-1 的推论。

   给其中一行乘上 \(k\)，使得两行相等，行列式为 \(0\)，所有原行列式为 \(0\)。

显然？感性理解。

性质 \(5\) 的推论。

行列式变换

1. 交换任意两行，行列式变号。
2. 把某一行乘上 \(k\) 加到另一行去，行列式不变。

类似高斯消元。操作复杂度 \(O(n^3)\)。

对于第 \(i\) 行，它的第 \(1 \sim i-1\) 列都是 \(0\)，用它把 \(i+1 \sim n\) 行的第 \(i\) 列清零。

枚举 \(i,j\)，每次单词操作是 \(O(n)\) 的，一共 \(O(n^3)\)。

模板题：P7112 【模板】行列式求值

模板题答案要对一个数 \(p\) 取模。而且 \(p\) 还不是质数。当 \(a,p\) 非互质的时候，\(a\) 在模 \(p\) 意义下没有逆元。

因此我们只能使用辗转相除法。

用第 \(i\) 行去清空第 \(j\) 行的第 \(i\) 列时，我们让这两行辗转相除，一共要做 \(O(\log)\) 次操作。

乍一看是 \(O(n^3 \log)\) 的，但是可以证明第 \(i\) 行和 \(i+1 \sim n\) 行一共只会做 \(O(\log)\) 次辗转相除，因为每次值至少被减少一半。

所有这道题的时间复杂度是 \(O(n^2 \log + n^3)\) 的。

#include<bits/stdc++.h>
#define sf scanf
#define pf printf
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
using namespace std;
typedef long long ll;
namespace hanglieshi {
    constexpr int N=607;
    int n,p,a[N][N],f;
    int add(int a,int b) { return a+b>=p ? a+b-p : a+b; }
    void _add(int &a,int b) { a=add(a,b); }
    int mul(int a,int b) { return 1ll*a*b%p; }
    void _mul(int &a,int b) { a=mul(a,b); }
    void _swap(int x,int y) {
        rep(i,1,n) swap(a[x][i],a[y][i]);
        f^=1;
    }
    void gauss() {
        rep(i,1,n) {
            rep(j,i+1,n) {
                while(a[i][i]) {
                    int K=a[j][i]/a[i][i];
                    rep(k,i,n) {
                        _add(a[j][k],p-mul(K,a[i][k]));
                    }
                    _swap(i,j);
                }
                _swap(i,j);
            }
        }
    }
    int calc() {
        int ans=1;
        rep(i,1,n) _mul(ans,a[i][i]);
        return f ? add(p,-ans) : ans;
    }
    void main() {   
        sf("%d%d",&n,&p);
        rep(i,1,n) rep(j,1,n) sf("%d",&a[i][j]), (a[i][j]+=p)%=p;
        gauss();
        pf("%d\n",calc());
    }
}
int main() {
    #ifdef LOCAL
    freopen("in.txt","r",stdin);
    freopen("my.out","w",stdout);
    #endif
    hanglieshi :: main();
}

余子式和 Laplace 展开

待补充

积和式

就是行列式没掉 \(-1\) 那个系数。

\[\det(A) = \sum_{\sigma \in S_n} \prod_{i=1}^n a_{i,\sigma_i} \]

积和式的计算是 NP 的。

判定积和式是否为 \(0\) 有一个正确率很高的方法。

我们可以根据下面的定理：

或者根据直觉（。

我们转为判断原方阵的行列式是否为 \(0\)。这有可能出现行列式为 \(0\) 但是积和式不为 \(0\) 的情况。因此我们随机一下方阵里面的数（大概是指 shuffle 以下行的顺序？或者应该是指随机一下边权吧？）。我们合理认为多做几次就是正确的。

比内·柯西公式 Cauchy binet formula

对于一个 \(s \times n\) 的矩阵 \(A\) 和 \(n \times s\) 的矩阵 \(B\)，（\(n \ge s\)）有：

\[|AB| = \sum |A_s|\cdot |B_s| \]

其中 \(A_s,B_s\) 指在矩阵 \(A\) 里选择 \(s\) 行，在矩阵 \(B\) 里选择集合相同的 \(s\) 列，形成的方阵。

---

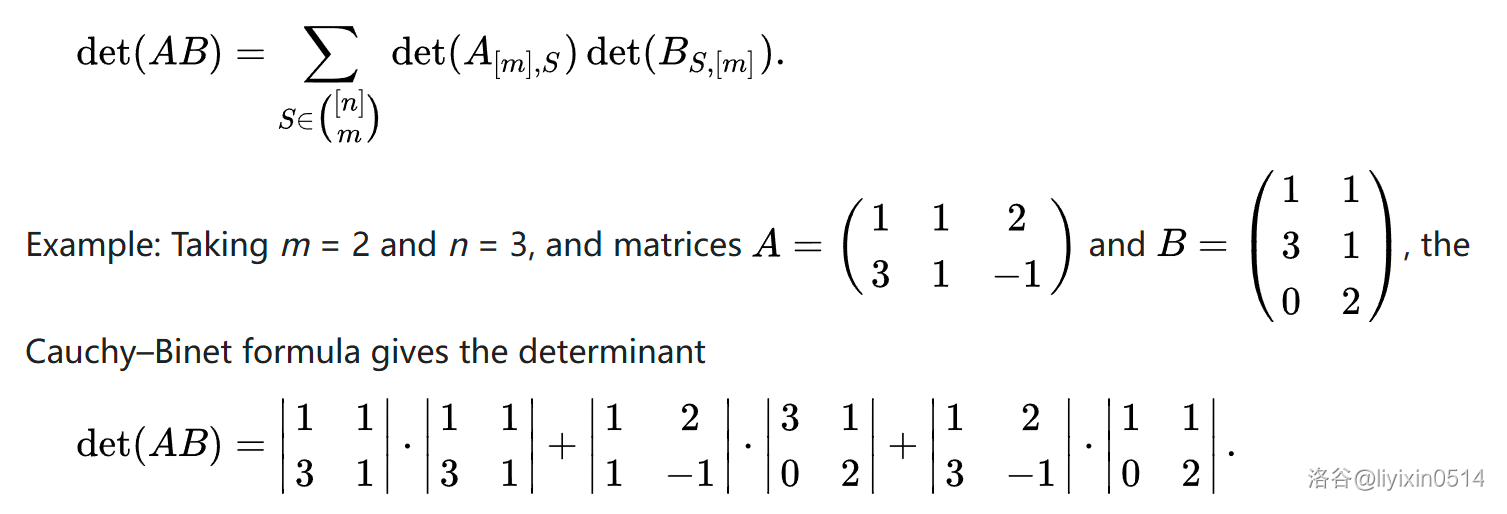
例题：#3409. 「2020-2021 集训队作业」Yet Another Linear Algebra Problem

参考题解 [LOJ 3409] Yet Another Linear Algebra Problem。

其中 \(GF(p)\) 的意思是在模 \(p\) 剩余系意义下。

问题一相当于从 \(n\) 个向量里选择 \(m\) 个向量，形成一个方阵。求满秩的方阵个数。

在模 \(3\) 意义下，非满秩的方阵的行列式值 \(=0\)，满秩的方阵的行列式值 \(\in\{1,2\}\)。

发现在模 \(3\) 意义下，\(1,2\) 的平方都是 \(1\)。

\(X\) 表示所有向量形成的 \(n\) 行 \(m\) 列的矩阵。

使用比内柯西公式，答案就是 \(|X^TX|\)。

问题二的话，我们再搞一个矩阵处理颜色限制。矩阵 \(A\)，定义 \(A_{i,j}\in \{0,1\}\) 表示向量 \(i\) 是否是颜色 \(j\)。这是一个 \(n\) 行 \(m\) 列的矩阵。

答案就是 \(|A^TX|\)。

时间复杂度 \(O(n^3)\)。(\(n,m\) 同阶)

code。