闵可夫斯基和

闵可夫斯基和

前言

部分图片来自 https://www.luogu.com.cn/article/mhp0aeub，最初来源未知。

定义

对于两个向量集合 \(A,B\)，它们的闵可夫斯基和为 \(\{ a+b | a \in A, b \in B\}\)。

求解

在 OI 中，我们一般研究凸包的闵可夫斯基和。

如图是两个凸包的闵可夫斯基和。

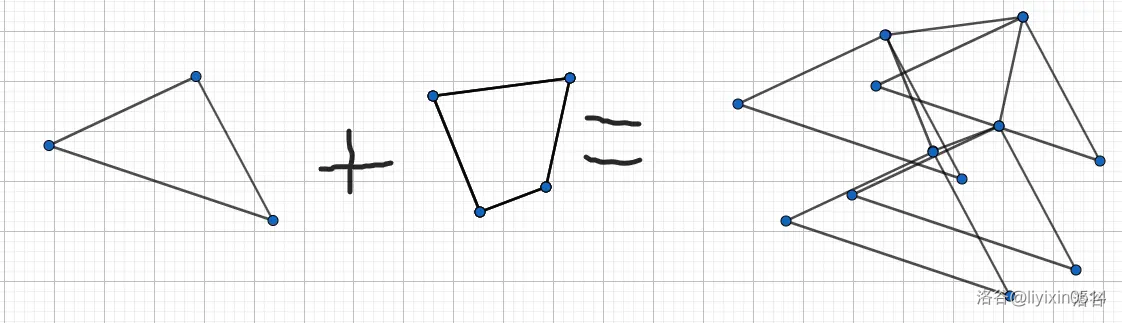
对它们的闵可夫斯基和求个凸包（因为通常问题只需要维护凸包），发现点数是 \(n+m\) 的，而且每条边刚好都是原凸包的边平移得到。进一步，实际上闵可夫斯基和的凸包其实就是两个凸包的所有边按照斜率进行归并排序。可以 \(O(n+m)\) 求出。

具体为什么这样可以感觉一下，容易发现是对的。

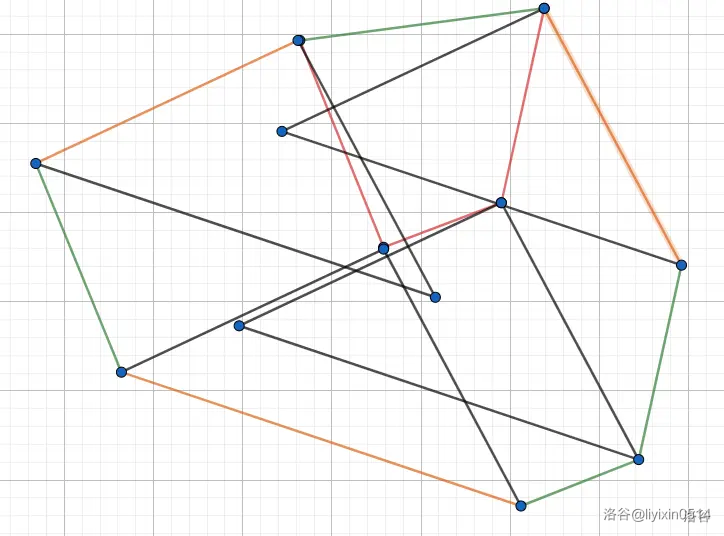
哇，就一个归并排序，讲完啦。

例题

P4557 [JSOI2018] 战争

相当于问两个凸包，其中一个凸包平移一个向量之后它们是否有交。考虑求出使得两个凸包有交的移动向量的范围。

我们求出哪些向量会使得两个凸包移动后相切，就可以求出范围了。

就是对于每个 \(a \in A, b \in B\)，求出集合 \(W= \{ w | a+w = b \}\)，然后求 \(W\) 的凸包，在凸包内的所有向量都会使得 \(A,B\) 平移后有交。

即求 \(B,-A\) 的闵可夫斯基和。然后对于每次询问判定向量是否在凸包内。

code