【20zr提高组十连测day10】信

【20zr提高组十连测day10】信

给定 \(n,m\)，\(n,m\le 10^5\)，给定分别长度为 \(n-1,m,n,m-1\) 的单调不减的序列 \(A,B,C,D\)，然后形如该图建边：

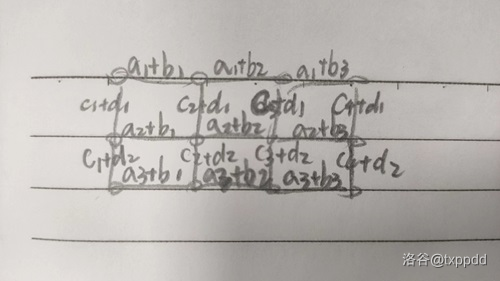
考虑到序列是递增的，对于除最左上角以外的每个点，每个点一定要选和自己相连的一条边才能形成一棵树。那么选择左边或上边一定是更优的，而且我们发现随便选择左边或上边，最终刚好都能形成一棵树。

这棵生成树就是最优的生成树，它的权值是 \(\sum \min(a_i+b_j,c_{i-1}+d_{j+1})\)。

这样比较丑陋，我们把 \(A,D\) 的标号右移以为，然后钦定 \(a_1=inf,d_1=inf\) 这样不影响正确性。

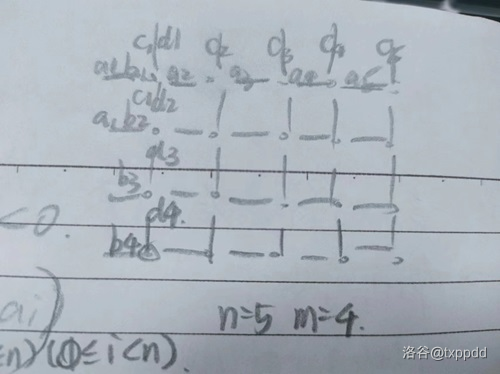
答案变成 \(\sum \min(a_i+b_j,c_i+d_j)\)。

如果我们选择第一项，说明 \(a_i+b_j\le c_i+d_j\)

\[ c_i+d_j-a_i-b_j \ge 0\\ (c_i-a_i)+(d_j-b_j)\ge 0\]

那么当 \((c_i-a_i)+(d_j-b_j)<0\) 的时候，我们会选择 \(c_i+d_j\) 这一项。

所以我们的答案式子可以很巧妙地变成：

\[\sum (a_i+b_j)+min(0,(c_i-a_i)+(d_j-b_j)) \]

如果 $(c_i-a_i)+(d_j-b_j)\ge 0 $，答案就取到第一项，否则刚好我们可以取到第二项。

\(a_i+b_j\) 可以 \(O(n+m)\) 算出，后面那部分排个序，然后扫描维护一下指针，也是 \(O(n)\)，详见代码。

#include<bits/stdc++.h>
// #define DEBUG
#define sf scanf
#define pf printf
#define int ll
#define rep(x,y,z) for(int x=(y);x<=(z);x++)
using namespace std;
typedef long long ll;
const int N=1e5+5,inf=3e6;
int n,m;
int a[N],b[N],c[N],d[N];
int w1[N],w2[N];
ll s;
ll ans;
signed main(){
    #ifdef DEBUG
    // freopen("ex_A1.in","r",stdin);
    freopen("in.txt","r",stdin);
    freopen("a.out","w",stdout);
    #endif
    sf("%lld%lld",&n,&m);
    rep(i,2,n) sf("%lld",&a[i]);
    rep(i,1,m) sf("%lld",&b[i]);
    rep(i,1,n) sf("%lld",&c[i]);
    rep(i,2,m) sf("%lld",&d[i]);
    a[1]=inf,d[1]=inf;
    ans-=min(a[1]+b[1],c[1]+d[1]);
    rep(i,1,n) ans+=a[i]*m,w1[i]=c[i]-a[i];
    rep(i,1,m) ans+=b[i]*n,w2[i]=d[i]-b[i],s+=w2[i];
    sort(w1+1,w1+n+1);
    sort(w2+1,w2+m+1);
    int r=m;
    rep(i,1,n){
        while(w2[r]+w1[i]>=0&&r>=1) {s-=w2[r];r--;}
        ans+=s+w1[i]*r;
    }
    pf("%lld\n",ans);
}