【20省选十联测day10】Cells Blocking

【20省选十联测day10】Cells Blocking

给你一个 \(n\times m\) 的网格，其中有一些格子被叉掉了，问再叉掉两个格子，使得从 \((1,1)\) 每次往右或者往下走，无法走到 \((n,m)\)，有几种叉格子的方式。

我们肯定是要一个 \(O(n^2)\) 的算法，而且不能带 \(\log\)。

如果 \((1,1)\) 和 \((n,m)\) 本来就不连通，直接特判掉。以下假设 \((1,1)\) 与 \((n,m)\) 连通。

找出两条路径，一条能往下走就往下走，否则往右走，另一条能往右走就往右走，否则往下，分别对应图中绿色、红色两条。

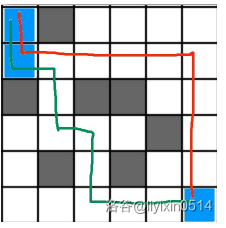
找这个路径的方式是，从 \((n,m)\) 搜出哪些点可以走到它，然后再从 \((1,1)\) 搜，如果下面/右边的点合法就走，否则走另一个方向。

两条路径的长度为 \(O(n)\)。我们叉点分两种情况。分为只叉一个点就可以达成目的，另一个点随便选；以及必须叉两个点才能达成目的。

只叉一个点，显然我们必须选择刚刚两条路径相交的那些部分，那些部分是割点，充分性显然，必要性也显然，如果你选了别的点，那么至少你可以走两条路径中的一条到达右下角，显然不合法。然后第二个点任选。

叉两个点的情况。首先我们可以在其中一条路径（如绿色路径）上选择一个不是两条路径的交点的点。把它叉了，然后更新（如绿色）路径，这样一次是 \(O(n^2)\) 的，总共 \(O(n^3)\)。发现重新更新（如绿色）路径很浪费时间，显然可以优化一下。我们叉掉了一个点，显然它左边和下面的点无法成为备选方案。新的路径一定是经过它的上边和右边的，且上边或右边至少一边有新点。我们考虑往某个方向找到一个合法的新点（指可以到达左上角和右下角），然后 \(O(n)\) 把新路径扩展出来。为了方便，我们往斜右上方找这个点，因为这个方向上一定有新点，而且这个方向上的点如果合法，在叉掉选定点之后，它仍然一定合法。

时间复杂度 \(O((n+m)^2)\)。题解说还有 \(O(nm)\) 的做法，但是我不会。

code

#include<bits/stdc++.h>
//#define LOCAL
#define sf scanf
#define pf printf
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
using namespace std;
typedef long long ll;
const int N=3e3+5;
char mp[N][N];
int n,m,s;
bool ok[2][N][N];
bool vi[N][N];
ll ans;
void dfs(int x,int y,int op) {
	if(vi[x][y]) return;
	vi[x][y]=1;
	if(mp[x][y]=='.') ok[op==-1?0:1][x][y]=1;
	else return;
	if(x+op>0&&x+op<=n) dfs(x+op,y,op);
	if(y+op>0&&y+op<=m) dfs(x,y+op,op);
}
int ud[N][N];
#define pii pair<int,int> 
#define fi first
#define se second
vector<pii > vec;
void dfs2(int x,int y,int op) {
	if(op) ud[x][y]=1;
	else vec.push_back({x,y});
	if(x==n&&y==m) return;
	if(!op) {
		if(x+1<=n&&ok[0][x+1][y]) dfs2(x+1,y,op);
		else dfs2(x,y+1,op);
	}else{
		if(y+1<=m&&ok[0][x][y+1]) dfs2(x,y+1,op);
		else dfs2(x+1,y,op);
	}
}
int main() {
	#ifdef LOCAL
	freopen("in.txt","r",stdin);
	freopen("my.out","w",stdout);
	#endif
	sf("%d%d",&n,&m);
	rep(i,1,n) {
		sf("%s",mp[i]+1);
		rep(j,1,m) s+=mp[i][j]=='.'?1:0;
	}
	dfs(n,m,-1);
	memset(vi,0,sizeof(vi));
	dfs(1,1,1);
	rep(i,1,n) rep(j,1,m) ok[0][i][j]&=ok[1][i][j];
	if(!ok[0][1][1]) {
		ans=1ll*s*(s-1)/2;
		pf("%lld\n",ans);
		return 0;
	}
	dfs2(1,1,0);dfs2(1,1,1);
	int ss=0;
	for(auto u:vec) {
		if(ud[u.fi][u.se]) ss++,ans+=s-1,ud[u.fi][u.se]=-1;
	}
	ans-=1ll*ss*(ss-1)/2;
	for(auto u:vec) {
		int x=u.fi,y=u.se;
		if(ud[x][y]==-1) {
			continue;
		}
		rep(i,1,n) {
			if(ok[0][x-i][y+i]) {
				if(ud[x-i][y+i]==1) ans++;
				for(int xx=x-i,yy=y+i;xx>1||yy>1;) {
					if(yy-1>0&&ok[0][xx][yy-1]) yy--;
					else xx--;
					if(ud[xx][yy]==1) ans++;
				}
				for(int xx=x-i,yy=y+i;xx<n||yy<m;) {
					if(xx+1<=n&&ok[0][xx+1][yy]) xx++;
					else yy++;
					if(ud[xx][yy]==1) ans++;
				}
				break;
			}
		}
	}
	pf("%lld\n",ans);
}