网络流
网络流
简介
存在源点 \(s\) 和汇点 \(t\) ,每条边给出容量 \(w\) ,求最大流 \(or\) 最小割。
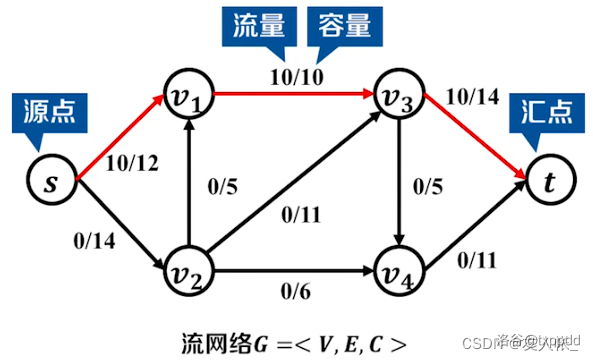
最大流
最大流即为从源点经其他节点流向汇点最大总流量。
从源点出发,找一条通向汇点的路线(即增广路线),使总流量增加。
重复直到源点汇点不连通(没有新的增广路线)。( dinic 算法原理)
Ford–Fulkerson 增广
Ford–Fulkerson 增广是计算最大流的一类算法的总称。该方法运用贪心的思想,通过寻找增广路来更新并求解最大流。——来自 OI Wiki
最小割 最大流定理
最小割即为删除某些边(代价为边的容量)使源点 \(s\) 与汇点 \(t\) 不连通,花费的最小代价。
最小割最大流定理:
最小割 \(=\) 最大流。
证明:若删完最大流流经的关键边(总代价 \(=\) 最大流)后,仍存在一条通路,则该通路可作为增广路线,原最大流不是最大流。证毕。
EK 算法
一次寻找增广路径流程如下:
\(fl_u\) 表示节点 \(u\) 可能流到的流量。再记录 \(from_u\) 表示 \(u\) 的流量是哪条边给的。
从源点开始,每个与 \(u\) 相连的节点如果没有被遍历过,那么它将获得 \(u\) 的所有流量。
一直遍历到 \(t\),增广路径流量即为 \(fl_t\)。然后从 \(t\) 一直追回 \(s\),调整路径所有边的容量。
一次找增补路线时间复杂度为 \(O(m)\),总增广次数不超过 \(O(nm)\),所以总时间复杂度为 \(O(nm^2)\)。
#include<bits/stdc++.h>
#define sf scanf
#define pf printf
#define int ll
using namespace std;
typedef long long ll;
const int N=205,M=5005;
const ll inf=0x3f3f3f3f3f3f3f3f;
int n,m,u,v,w,s,t;
int cnt=1,head[N];
struct edge{
int to,ne,cal;
}e[M<<1];
void add(int u,int v,int w){
e[++cnt]={v,head[u],w};
head[u]=cnt;
}
void addedge(int u,int v,int w){ add(u,v,w),add(v,u,0); }
int fl[N],fr[N];
int EK(int s,int t){
int flow=0;
while(1){
memset(fl,-1,sizeof(fl));
queue<int> q;
q.push(s);
fl[s]=inf;
while(!q.empty()){
int u=q.front();
q.pop();
if(u==t) break;
for(int i=head[u];i;i=e[i].ne){
int v=e[i].to;
if(e[i].cal&&fl[v]==-1){
fl[v]=min(e[i].cal,fl[u]);
fr[v]=i;
q.push(v);
}
}
}
if(fl[t]==-1) return flow;
flow+=fl[t];
for(int i=t;i!=s;i=e[fr[i]^1].to){
e[fr[i]].cal-=fl[t],e[fr[i]^1].cal+=fl[t];
}
}
}
signed main(){
sf("%lld%lld%lld%lld",&n,&m,&s,&t);
for(int i=1;i<=m;i++){
sf("%lld%lld%lld",&u,&v,&w);
addedge(u,v,w);
}
int flow=EK(s,t);
pf("%lld\n",flow);
}
dinic 算法 code
每次先 bfs 判断是否存在增补路线,及划分高度。
然后 dfs 求增补流的大小(按照划分好的高度搜),记住弧优化。(可以再加个减枝)
每次找增补路线时间为 \(O(m)\),最多找 \(f\) 次,即:
时间复杂度 \(O(m \cdot f)\) 或 \(O(n^2m)\),其中 \(f\) 为最大流量。
若 \(w_i=1(1\leq i\leq n)\) ,时间复杂度为 \(O(m\cdot \min (m^{\frac 1 2},n^\frac 2 3))\) 。
#include<bits/stdc++.h>
#define ll long long
#define pf printf
#define sf scanf
using namespace std;
const int N=1e3+5,M=1e5+7;
const int MAXX=1e9;
struct node {
int to,net;
ll val;
} e[M>>1];
int n,m,s,t;//n个点,m条边,起点为s,终点为t
ll w,dep[N];// dep 为层数(即 level )
int u,v;
int tot=1,now[N],head[N]; // now 用于当前弧优化
void addedge(int u,int v,ll w){//链式前向星存图
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
//求每个结点属于哪一层 && 是否存在从 s 到 t 的增补路线
int bfs(){
memset(dep,0,sizeof(dep));
queue<int> q;
while(!q.empty()) q.pop();
q.push(s);
dep[s]=1;
now[s]=head[s];
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i;i=e[i].net) {
int v=e[i].to;
if(e[i].val>0&&!dep[v]) {
q.push(v);
now[v]=head[v];
dep[v]=dep[u]+1;
if(v==t) return 1;
}
}
}
return 0;
}
//找增补路线
ll dfs(int u,ll sum){ // sum 表示给到 u 的剩余可支配流量
if(u==t) return sum;
ll k,res=0; // res 表示经过 u 的最大流量
for(int i=now[u];i&∑i=e[i].net) {
now[u]=i;
int v=e[i].to;
if(e[i].val>0&&(dep[v]==dep[u]+1)) {
k=dfs(v,min(sum,e[i].val)); // 给到 v 的剩余可支配流量即为 min( u 的剩余可支配流量,u->v 的容量 )
if(k==0) dep[v]=-1; // v 已经没有用了
e[i].val-=k; // 当前边容量减少
e[i^1].val+=k; // 反向边容量增加
res+=k; // 贡献流量增加
sum-=k; // 剩余可支配流量减少
}
}
return res;
}
ll dinic(){
ll maxflow=0,x;
while(bfs()){//不断寻找增补路线
while(x=dfs(s,MAXX)) maxflow+=x;
}
return maxflow;
}
int main(){
sf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++){
sf("%d%d%lld",&u,&v,&w);
addedge(u,v,w),addedge(v,u,0);//建双向边
}
pf("%lld\n",dinic());//输出最大流 or 最小割
}
预流推进 HLPP 算法
时间复杂度 \(O(n^2\sqrt m)\) 。
思路
先从 \(s\) 往相邻点拼命灌水,然后让水不停地向 \(t\) 流,能流多少是多少。有多少水流流到汇点,最大流就是多少。
算法流程
余流:当前结点有多少单位流。
HLPP 算法预处理出每个结点的高度,规定水只能往低一个单位的结点流。
- 先从 \(t\) 到 \(s\) 反向 bfs ,使每个点有一个初始高度(源点高度为 \(n\) ,汇点高度为 \(0\) )。
- 从 \(s\) 开始向外推流,将有余流的点放入栈。
- 不断从栈里取出高度最高的点进行推流操作。
- 若推完还有余流,更新高度标号,重新放入栈。
- 当栈为空时结束算法,最大流即为 \(t\) 的余流
gap 优化:
如果某个高度不存在,将所有比该高度高的节点标记为不可到达(使它的高度为 \(n+1\) ,这样就会直接向 \(s\) 推流了)。
HLPP 算法通过 bfs 预先处理了高度标号,并利用栈(或 vector 、 list )使得每次推流都是高度最高的顶点,以此减少推流的次数和重标号的次数。
code
#include<bits/stdc++.h>
#define ll long long
#define pf printf
#define sf scanf
using namespace std;
const int N=1201,M=120000;
const int inf=0x3f3f3f3f;
struct edge{
int to,val,ne;
}e[M*2+1];
int head[N],dep[N];//dep[i] 表示结点 i 到 t 的最小距离
stack<int> st[N];// st[i] 存 dep 值为 i 的有余流的结点
int gap[N];// gap[i] 表示 dep 值为 i 的结点个数
int ex[N];//余流
int cnt=1,level;//level 表示有余流的最高结点高度
int n,m,s,t,u,v,w;
void addedge(int u,int v,int w){//链式前向星存图
e[++cnt].val=w,e[cnt].to=v,e[cnt].ne=head[u];
head[u]=cnt;
}
bool bfs(){// 从 t 开始反向 bfs
memset(dep,0x3f,sizeof(dep));
dep[t]=0;
queue<int> q;
q.push(t);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i;i=e[i].ne){
int v=e[i].to,w=e[i^1].val;
if(w&&dep[v]>dep[u]+1) dep[v]=dep[u]+1,q.push(v);
}
}
return dep[s]!=inf;//可以到达 s
}
void flow(int u,int v,int id,int f){//从 u 向 v 流入 f 单位流(经过边 id)
ex[u]-=f,ex[v]+=f;
e[id].val-=f,e[id^1].val+=f;
}
int push(int u){// 推 u 的余流
for(int i=head[u];i;i=e[i].ne){
int v=e[i].to,w=e[i].val;
if(dep[u]!=dep[v]+1&&u!=s||!w||dep[v]==inf) continue;//推流至高度减一的结点
if(v!=s&&v!=t&&!ex[v]) st[dep[v]].push(v),level=max(level,dep[v]); // v 原先余流为 0
flow(u,v,i,u==s?w:min(w,ex[u])); //推流
if(!ex[u]) return 0; // 无剩余
}
return 1; //有剩余
}
int choose(){//选择当前有余流的高度最高的结点
while(st[level].empty()&&level>=0) level--;
return level==-1?0:st[level].top();
}
void change(int u){//更新高度
if(!--gap[dep[u]]){//gap 优化 (出现断层)
for(int i=1;i<=n;i++){
if(dep[i]>dep[u]&&dep[i]<=n&&i!=s){
dep[i]=n+1;//将所有高度大于 dep[u] 的结点设为不可到达
}
}
}
dep[u]=inf;
for(int i=head[u];i;i=e[i].ne){
int v=e[i].to,w=e[i].val;
if(w) dep[u]=min(dep[u],dep[v]);
}
if(++dep[u]<n){//dep[u] 更新为可到达的结点中最小高度再高一个单位
st[dep[u]].push(u);
level=max(level,dep[u]);
gap[dep[u]]++;
}
}
int HLPP(){
if(!bfs()) return 0; //无法从 s 到 t
dep[s]=n;
for(int i=1;i<=n;i++){
if(dep[i]!=inf)
gap[dep[i]]++;
}
push(s);//将 s 可到达的结点推满
int u;
while(u=choose()){//选择最高有余流结点
st[level].pop();
if(push(u)){//推流
change(u);//若有余流则提高高度
}
}
return ex[t];// t 的余流即为最大流
}
int main(){
sf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++){
sf("%d%d%d",&u,&v,&w);
addedge(u,v,w),addedge(v,u,0);// 建双向边
}
pf("%d\n",HLPP());//HLPP 求最大流
}
最小费用最大流
即求满足最大流前提下,同时满足最小费用。
问 \(max_{flow}\) 和 \(min_{fee}\) 。
SCC 算法
SCC 算法基于 Dinic 和 SPFA 的实现
把找增补路线的 bfs 换成 SPFA,\(dis_s=0,dep_u=dis_u\) 即可。
每次找增补路线时间为 \(O(nm)\),最多找 \(f\) 次,总时间复杂度约为 \(O(nmf)\)。
#include<bits/stdc++.h>
#define sf scanf
#define pf printf
using namespace std;
typedef long long ll;
const int N=5e3+5,M=5e4+5,inf=0x3f3f3f3f;
int n,m,u,v,w,c;
int cnt=1,head[N],cur[N];
int s,t;
struct edge{
int to,ne,cal,val;
}e[M<<1];
void add(int u,int v,int w,int c){
e[++cnt]={v,head[u],w,c};
head[u]=cnt;
}
void addedge(int u,int v,int w,int c) { add(u,v,w,c),add(v,u,0,-c); }
int flow,cost;
bool vi[N];
int dis[N];
bool spfa(int s,int t){
queue<int> q;
memset(dis,0x3f,sizeof(dis));
memcpy(cur,head,sizeof(cur));
vi[s]=1;
q.push(s);
dis[s]=0;
while(!q.empty()){
int u=q.front();
q.pop();
vi[u]=0;
for(int i=head[u];i;i=e[i].ne){
int v=e[i].to,c=e[i].cal,w=e[i].val;
if(c&&dis[u]+w<dis[v]){
dis[v]=dis[u]+w;
if(!vi[v]) vi[v]=1,q.push(v);
}
}
}
return dis[t]!=inf;
}
int dfs(int u,int t,int fl){
if(u==t) return fl;
vi[u]=1;
int ans=0;
for(int &i=cur[u];i&&ans<fl;i=e[i].ne){
int v=e[i].to,c=e[i].cal,w=e[i].val;
if(!vi[v]&&c&&dis[u]+w==dis[v]){
int x=dfs(v,t,min(c,fl-ans));
if(x) ans+=x,e[i].cal-=x,e[i^1].cal+=x,cost+=w*x;
else dis[v]=-1;
}
}
vi[u]=0;
return ans;
}
int mfmc(int s,int t){
int flow=0;
while(spfa(s,t)){
int x;
while(x=dfs(s,t,inf)) flow+=x;
}
return flow;
}
int main(){
sf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;++i){
sf("%d%d%d%d",&u,&v,&w,&c);
addedge(u,v,w,c);
}
flow=mfmc(s,t);
pf("%d %d\n",flow,cost);
}
经验
P2766 最长不下降子序列问题
-
显然 DP 求解。
设 \(f_i\) 表示以 \(i\) 结尾最长不下降子序列长度。
暴力求解时间复杂度 \(O(n^2)\) ,如果用树状数组优化可以降至 \(O(nlogn)\) ,不过显然本题可以直接暴力。 -
可以想到建流求解。( $ (u,v,w) $ 表示建一条从 \(u\) 到 \(v\) 边权为 \(w\) 的边,同时建边权为 \(0\) 的反向边)
- 每个点只能用一次,因此将所有 \(i\) 拆成两个点 \(i_x,i_y\) ,并建边 \((i_x,i_y,1)\)
- \(f_i=1\ \Rightarrow (S,i_x,1)\)
- \(f_i=\max(f_x)\ \Rightarrow (i_y,T,1)\)
- 在 DP 过程中,对于每个 \(f_i\gets f_j+1 \ \Rightarrow (j_y,i_x,1)\)
求最大流即可。
- 将边 \((S,1_x),(n_y,T),(1_x,1_y),(n_x,n_y)\) 权赋值为
inf即可。
lis (伪网络流题)
题意:给你一个长度为 \(n\) 的序列,求满足最长上升子序列长度小于原序列的最长上升子序列长度的子序列(不要求连续区间)的最大长度。
- DP 求解最长上升子序列, \(f_i\) 表示以 \(i\) 结尾的最长上升子序列长度,用树状数组优化,时间复杂度 \(O(nlogn)\) 。
- 建流求解。最小割即为最少需要删去的结点个数。时间复杂度为 \(O(m\cdot \min (m^{\frac 1 2},n^\frac 2 3))\) 。
- \(f_i=1 \ \Rightarrow (S,i,1)\)
- \(f_i=\max(f_x)\ \Rightarrow (i,T,1)\)
- 在 DP 过程中,对于每个 \(f_i\gets f_j+1\ \Rightarrow (j,i,1)\)
- 显然,对于 \(f_j=f_j,i<j\) ,必定有 \(a_i>a_j\) 。(否则 \(f_j\) 将加 \(1\) )
那么将所有 \(f_x=k,1\leq k\leq n\) 分别按下标从小到大排序,则满足 \(i<i',a_i<a_{i'}\) 必定在一个连续区间 \([l_i,r_i]\) ,且对于每个 \(f_j=f_i,j>i\) ,有 \(l_j\ge l_i,r_j\ge r_1\) 。证明略。(自己想象)即下图。
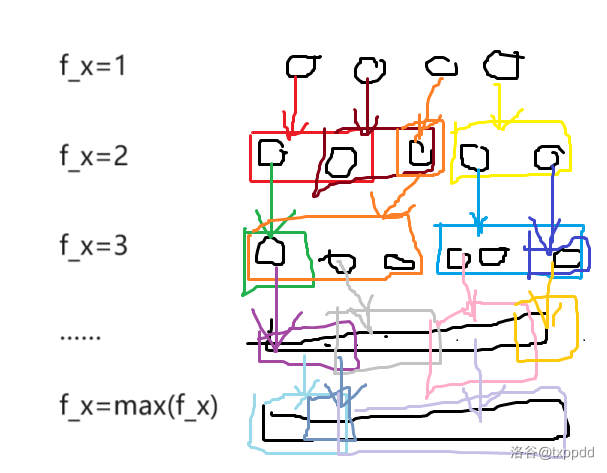
因此该网络流无需退流,所以不必建流。仅需在每一层记录一个指针表示当前只能从指针处开始选择,统计能到达最底层的数量即可。
本文来自博客园,作者:liyixin,转载请注明原文链接:https://www.cnblogs.com/liyixin0514/p/18357750

