连通性相关

连通性相关

在有向图中，\(low_u\) 的定义一般指点 \(u\) 能到达的最小时间戳。在无向图中，\(low_u\) 的定义一般指点 \(u\) 不经过它与父亲的树枝边，至多走一条非树枝边，能到达的最小时间戳。

强连通分量

强连通的定义是：有向图 \(G\) 强连通是指，\(G\) 中任意两个结点连通。

强连通分量（Strongly Connected Components，SCC）的定义是：极大的强连通子图。——摘自 OI Wiki

Tarjan

用 Tarjan 求强连通分量（缩点），缩点后有向图变为一个 DAG。

算法简介

参考博客

定义

如果有向图 \(G\) 的每两个顶点都强连通，称 \(G\) 是一个强连通图。有向非强连通图的极大强连通子图，称为强连通分量。

四条边

树枝边： dfs 搜索树上的边。

前向边：与 dfs 方向一致，从某个结点指向其某个子孙的边。

后向边：与 dfs 方向相反，从某个结点指向其某个祖先的边。（返祖边）

横叉边：从某个结点指向搜索树中的另一子树中的某结点的边。

流程

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。

搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义 \(dfn(u)\) 为节点 \(u\) 搜索的次序编号(时间戳)， \(low(u)\) 为 \(u\) 或 \(u\) 的子树能够追溯到的最早的栈中节点的次序号。

由定义可以得出， \(low(u)=\min (low(u), low(v) )\) 。 \((u,v)\) 为树枝边， \(u\) 为 \(v\) 的父节点 。

  • 节点 \(v\) 可以到达 \(low(v)\) ，节点 \(u\) 为父亲，所以节点 \(u\) 也可以到达 \(low(v)\) 。

\(low(u)=\min (low(u), dfn(v) )\) 。 \((u,v)\) 为指向栈中节点的后向边/横叉边。

  • 因为此时 \(v\) 还在栈中，所以 \(low(v)\) 一定是 \(LCA(u,v)\) 的祖先。

当结点 \(u\) 搜索结束后，若 \(dfn(u)=low(u)\) 时，则以 \(u\) 为根的搜索子树上所有还在栈中的节点是一个强连通分量（ pop 一直到 \(u\) 就行）。

  • 当 \(dfn(u)=low(u)\) 时：

若子树里的点还在，则 \(low(v)\) 一定等于 \(dfn(u)\) 。子树的所有点可以到达 \(u\) ， \(u\) 可以到达子树所有点。

SCC-Tarjan模板

void tarjan(int u) {
    dfn[u]=low[u]=++dfn0;
    st[++top]=u;
    for(int v : to[u]) {
        if(!dfn[v]) {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }else if(!num[v]) {
            low[u]=min(low[u],low[v]);//与 dfn[v] 等价
        }
    }
    if(low[u]==dfn[u]) {
        ++cnt;
        while(st[top+1]!=u) scc[cnt].push_back(st[top]), num[st[top]]=cnt, --top;
    }
}

模板题：B3609 [图论与代数结构 701] 强连通分量

模版题2：受欢迎的牛

例题

CF427C

code
#include<bits/stdc++.h>
#define ll long long
#define pf printf
#define sf scanf
using namespace std;
const int N=1e5+7,mod=1e9+7;
int n,m;
int u,v;
vector<int> son[N];
int num; 
int c[N];
int dfn[N],low[N],scc[N]; 
int cnt,sum; 
int val[N];
ll ans,ans2=1;
int st[N],top; 
void Tarjan(int u){
	dfn[u]=low[u]=++num;
	st[++top]=u; 
	for(int i=0;i<son[u].size();i++){
		int v=son[u][i];
		if(!dfn[v]){
			Tarjan(v);
			low[u]=min(low[u],low[v]);
		}else if(!scc[v]){ 
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(low[u]==dfn[u]){
		scc[u]=++cnt;
		val[cnt]=c[u];
		sum=1;
		while(st[top]!=u){
			scc[st[top]]=cnt;
			if(c[st[top]]<val[cnt]) sum=1;
			else if(c[st[top]]==val[cnt]) sum++;
			val[cnt]=min(val[cnt],c[st[top]]);
			top--;
		}
		top--;
		ans+=val[cnt];
		ans2=ans2*sum%mod;
	}
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>c[i];
	}
	cin>>m;
	for(int i=1;i<=m;i++){
		cin>>u>>v;
		son[u].push_back(v);
	}
	for(int i=1;i<=n;i++)
		if(!dfn[i])
		Tarjan(i);
	pf("%lld %lld\n",ans,ans2);
}

Kosaraju

求一个无向图的强连通分量的方法是枚举每个点 i，如果还没有访问过点 i，就 dfs(i)，然后把 dfs 过程中的点缩到一个 SCC。

借鉴无向图的方法，可以发现在有向图上这种方法仍然正确当且仅当我们按照（假设已经缩完点的）DAG 的拓扑序反序 dfs。否则一个强连通分量将搜到另一个强连通分量，然后它们两回合在一起，显然不对。

如何找到 dfs 的正确顺序呢？我们以 1 开始进行 dfs，每个节点出栈时 push 到 st 数组（其实是栈）中，按照 st 的倒序求 SCC 就是正确的。

因为假设强连通分量 u 可以到达强连通分量 v，那么 v 会先进入 st，求 SCC 时按照倒序就会先求 v，这样求 u 时就不会搜到 v 了。

求 SCC 的方法和无向图一样。

总结：

  1. dfs(1)，st 记录结点出栈顺序。
  2. 按 st 的倒序 dfs，可以搜到的即为一个 SCC。

双连通分量

在一张连通的无向图中，对于两个点 \(u\) 和 \(v\)，如果无论删去哪条边（只能删去一条）都不能使它们不连通，我们就说 \(u\) 和 \(v\) 边双连通。

在一张连通的无向图中，对于两个点 \(u\) 和 \(v\)，如果无论删去哪个点（只能删去一个，且不能删 \(u\) 和 \(v\) 自己）都不能使它们不连通，我们就说 \(u\) 和 \(v\) 点双连通。

边双连通具有传递性，即，若 \(x,y\) 边双连通，\(y,z\) 边双连通，则 \(x,z\) 边双连通。

点双连通不具有传递性，反例如下图，\(A,B\) 点双连通，\(B,C\) 点双连通，而 \(A,C\) 不点双连通。

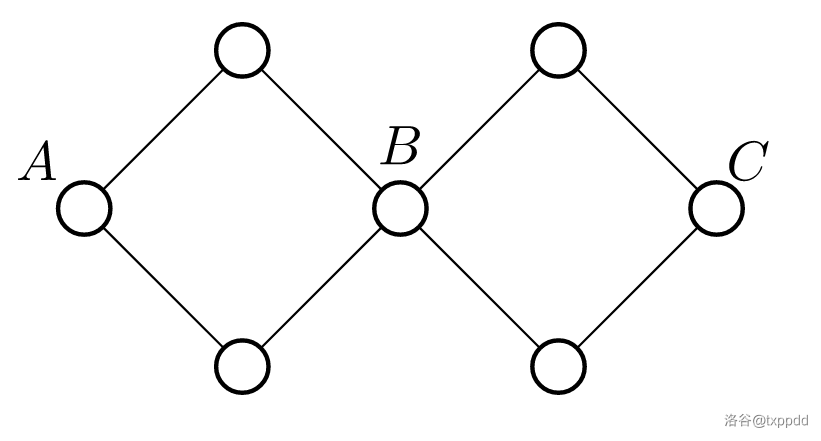
边双连通分量

在一张连通的无向图中，对于两个点 \(u\) 和 \(v\)，如果无论删去哪条边（只能删去一条）都不能使它们不连通，我们就说 \(u\) 和 \(v\) 边双连通。

边双连通具有传递性，即，若 \(x,y\) 边双连通， \(x,z\) 边双连通，则 \(y,z\) 边双连通。

两个点是边双连通的，当且仅当它们的图上路径中不包含桥。（如果没遍历过并且连的边不是割边就标记为同一块边双）

边双连通分量就是极大边双连通块。

无向图边双缩点后成为一棵树，所有树边是桥。

求出所有割边即可。

可以用 Tarjan。

P8436 【模板】边双连通分量

注意模板题有重边，因此 \(low_u\) 的定义是不经过上一次走过的边，走至多一条非树枝边可以到达的最小时间戳。

void tarjan(int u,int la) {
	dfn[u]=low[u]=++dfn0;
	st[++top]=u;
	for(auto i : to[u]) {
		int v=i.se;
		if(!dfn[v]) {
			tarjan(v,i.fi);
			low[u]=min(low[u],low[v]);
		}else if(i.fi!=la) {
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(low[u]==dfn[u]) {
		++cnt;
		num[u]=cnt, vec[cnt].push_back(u);
		while(st[top]!=u) num[st[top]]=cnt, vec[cnt].push_back(st[top]), --top;
		--top;
	}
}

点双连通分量

一个点可以属于多个点双。

Tarjan 求点双。

RT，黑色边为树边，红色边为返祖边。（由于是无向图，因此没有横叉边）

设 \(dfn_u\) 为 \(u\) 的时间戳，\(low_u\) 表示点 \(u\) 不经过父亲可以到达的最小时间戳。

若 \(v\) 是 \(u\) 的儿子，\(low_v=dfn_u\)，则 \(u,v\) 属于同一个点双，\(u\) 为该点双时间戳最小的节点，退栈加入该点双直到退掉 \(v\)，将 \(u\) 加入点双但是不退栈 \(u\)。

割点和桥

割点和桥一般针对无向图，因此没有横叉边。

桥

对于一个无向图，如果删掉一条边后图中的连通分量数增加了，则称这条边为桥或者割边。

RT，\((1,2)\) 即为该图唯一的桥。

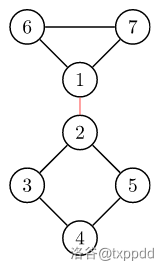
计算桥（割边）的方法：

首先，容易知道割边一定是 DFS 树的树边。记录 DFS 树上指向 \(v\) 的边，它是割边当且仅当以 \(v\) 为根的子树内没有向其它子树或祖先连边。
如果 \(v\) 的后代只能连回 \(v\) 自己。即 \(low(v) > dfn(u)\) ，则 \(u-v\) 是桥。

code

代码不保证正确

void tarjan(int rt,int u,int f) {
    dfn[u]=low[u]=++cnt;
    for(int v : to[u]) {
        if(!dfn[v]) {
            tarjan(rt,v,u), low[u]=min(low[u],low[v]);
            if(low[v]>dfn[u]) ans.push_back({u,v});
        }else if(v!=f) low[u]=min(low[u],dfn[v]);
    }
}

割点

对于一个无向图，如果把一个点删除后这个图的极大连通分量数增加了，那么这个点就是这个图的割点（又称割顶）。

RT，\(2\) 即为该图唯一的割点。

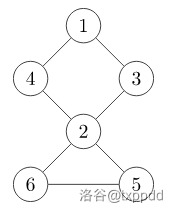
Tarjan 求割点。

\(low_u\) 表示点 \(u\) 经过至多一条非树边可以到达的最小时间戳。

计算割点的方法：

  1. 对于 DFS 树的树根，它是割点当且仅当它有两个及以上的子树。
  2. 对于其它任意一个点，当且仅当以它为根的子树内没有向其它子树或祖先连边。因此在 dfs 过程中，如果一个点 \(u\) 存在一个子节点 \(v\) ，使得 \(v\) 的后代只能连回 \(u\) 。即 \(low(v) \ge dfn(u)\) ，则 \(u\) 是割点。

Code

割点和割边代码唯一的区别就是 \(low_v > dfn_u\) 和 \(low_v \ge dfn_u\)。以及割点需要多判一个根。

void tarjan(int rt,int u,int f) {
	dfn[u]=low[u]=++cnt;
	int son=0;
	for(int v : to[u]) {
		if(!dfn[v]) {
			++son, tarjan(rt,v,u), low[u]=min(low[u],low[v]);
			if(low[v]>=dfn[u] && u!=rt && !isans[u]) isans[u]=1, ans.push_back(u);
		}else if(v!=f) low[u]=min(low[u],dfn[v]);
	}
	if(son>=2 && u==rt) isans[u]=1, ans.push_back(u);
}

圆方树

圆方树可以用来解决将无向图按点双缩点，但是原来的点的信息仍要保留的问题。（不像强连通分量缩点有的可以直接删除圆点，仅保留强连通分量编号）

将一个无向图变为一棵树：

把每个点双建一个方点，将点双中所有点建一个圆点，与该方点相连。

RT.

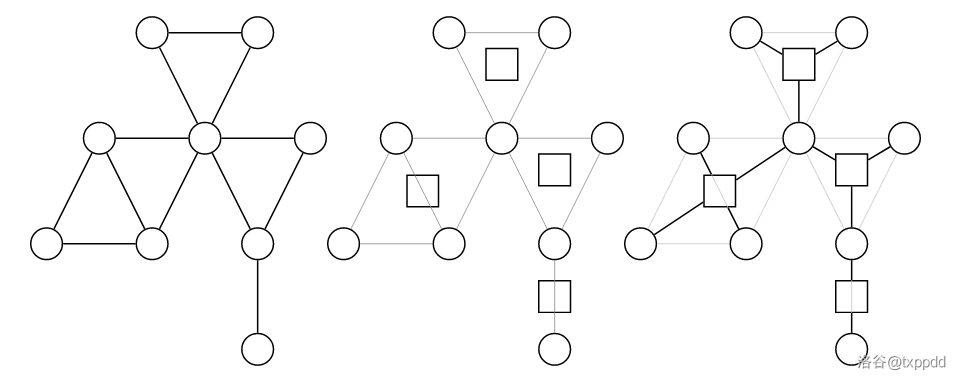
圆方树中，每条链一定是由圆点、方点交错形成。

建好圆方树后，依题意在树上求解即可。

Code

点双改一点即可。（代码为外向树，建双向边关掉注释即可）

void Tarjan (int u) {
	dfn[u]=low[u]=++cnt;
	st[++top]=u;
	for(int i=head[u];i;i=e[i].ne) {
		int v=e[i].to;
		if(!dfn[v]) {
			Tarjan(v);
			low[u]=min(low[u],low[v]);
			if(dfn[u]==low[v]) {
				tot++;
				to[u].push_back(tot);
//				to[tot].push_back(u);
				while(st[top]!=v){
					to[tot].push_back(st[top]);
//					to[st[top]].push_back(tot);
					top--;
				}
				to[tot].push_back(v);
//				to[v].push_back(tot);
				top--;
			}
		}else{
			low[u]=min(low[u],dfn[v]);
		}
	}
}

经验

演唱会

圆方树、点双。

posted @ 2024-08-13 21:26  liyixin  阅读(8)  评论(0)  编辑  收藏  举报