24ab-day8 洄游

24ab-day8 洄游

• 双倍经验：試験 (Examination)（双倍经验可参考这篇博客）

看到区间询问，我们自然可以想到莫队和分块，莫队是好做的，分块不好说，可以莫队的根号无法通过此题。

显然这是一个三维偏序问题，\(q\) 次询问，给定 \(l,r,k\)，问满足 \(l\le L,r\ge R,k\le K\) 的点的个数 \((K=R-L)\)。

三维偏序我们会陌上花开！CDQ 分治要 \(O(n\log ^2 n)\)，可惜这题 \(n\le 10^6\)，两只 \(\log\) 显然过不了（除非你极限卡常，然而我不会）。

发现第三维是前两位之差，这种东西一般可以通过容斥变成二位偏序问题，画个图出来会好想很多。

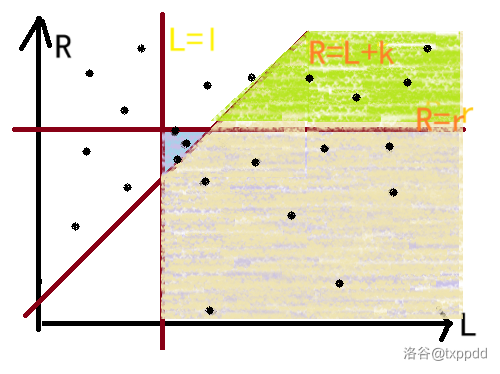
我们要求的就是浅蓝色的点数，即 \(l\le L,r\ge R,k\le R-L\)。容斥一下，加上紫色，减去黄色，再加上绿色。就是这样：

\[+(L\ge l,R\le r)\\ -(L\ge l,K<k)\\ +(R>r,K<k) \]

做三次二位偏序，时间复杂度 \(O(n\log n)\)。

code

#include<bits/stdc++.h>
// #define LOCAL
#define sf scanf
#define pf printf
#define isdigit(x) (x>='0'&&x<='9')
#define rep(x,y,z) for(int x=y;x<=z;x++)
using namespace std;
typedef long long ll;
const int N=1e6+5;
inline void read(int &x){
    x=0;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar());
    for(;isdigit(ch);ch=getchar()) x=(x<<3)+(x<<1)+ch-'0';
}
inline void _write(int x){
    static int st[7];
    int top=0;
    do{st[top++]=x%10,x/=10;}while(x);
    while(top) putchar(st[--top]+'0');
}
inline void write(int x,char c){
    _write(x),putchar(c);
}
int n,q;
int l,r,k;
struct node{
    int id,l,r,k;
}a[N<<1];
int ans[N];
struct tree{
    int tr[N];
    void add(int x,int val=1) {
        for(;x<=n;x+=x&-x) tr[x]+=val;
    }
    int ask(int x) {
        int s=0;
        for(;x;x-=x&-x) s+=tr[x];
        return s;
    }
}T,T1,T2;
int m=0;
int main(){
    #ifdef LOCAL
    freopen("in.txt","r",stdin);
    freopen("my.out","w",stdout);
    #endif
    read(n),read(q);
    rep(i,1,n) {
        read(l),read(r);
        a[++m]={0,l,r,r-l};
    }
    rep(i,1,q){
        read(l),read(r),read(k);
        if(r-l>=k) a[++m]={i,l,r,k-1};
    }
    sort(a+1,a+m+1,[](node a,node b){return a.l==b.l?a.id<b.id:a.l>b.l;});
    rep(i,1,m){
        if(a[i].id==0) T.add(a[i].r);
        else ans[a[i].id]+=T.ask(a[i].r);
    }
    sort(a+1,a+m+1,[](node a,node b) {return a.k==b.k?a.id<b.id:a.k<b.k;});
    rep(i,1,m){
        if(a[i].id==0) T1.add(a[i].l),T2.add(a[i].r);
        else ans[a[i].id]+=T1.ask(a[i].l-1)-T2.ask(a[i].r);
    }
    rep(i,1,q) write(ans[i],'\n');
}