2024牛客多校第四场F.Good Tree 挑战全网最详解

好吧标题党了一回，但我相信有不少人被出题人的那句“手玩一下就知道了”无语住了

像我这种憨憨一旦想偏了就救不回来了，于是困惑了好久，在雨巨的指导下彻底搞懂

（此处大声谢谢雨巨，又有实力又会讲题又认真答疑每一个问题，呜呜呜我永远的姐）

题意简单来说就是定义f(i)为树上i点到其他所有点的距离之和，给定x，要求构造一棵树使得存在点u，v满足f(v)-f(v)=x，且所用的节点最少。

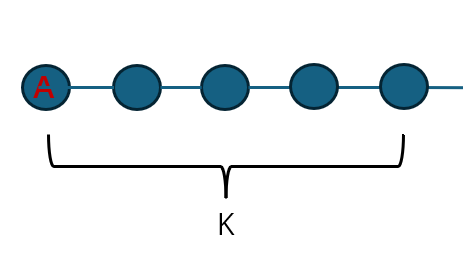
不妨把树上AB所在的路径拉出来，假设A子树里还有其他点，B子树里还有其他点

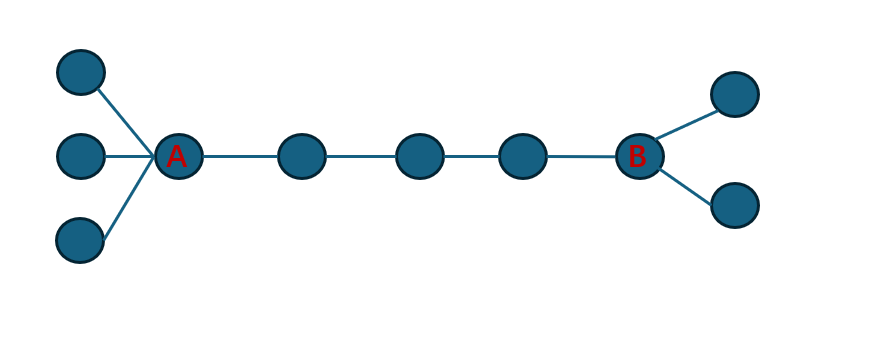
我们发现AB之间的点，因为有对称性，对A和B的贡献都是一样的

但是A子树中的点就不一定了，A到B一共要走4条边，A中有3个点，走到A的总贡献是3*1=3，走到B的总贡献是(1+4)*3=15

多了的12其实就是A子树中的点数*AB链上的边数=3*4=12

B子树同理，多了的部分是2*4=8

且在f(A)-f(B)中，A子树中的贡献是负值，也就是-12，B子树中的贡献是正值，也就是+8。

 

现在希望考虑极限情况，钦定f(A)的值能取到最大

 这时A的子树为空是最好的，因为它们只能贡献负数，那么就变成了：

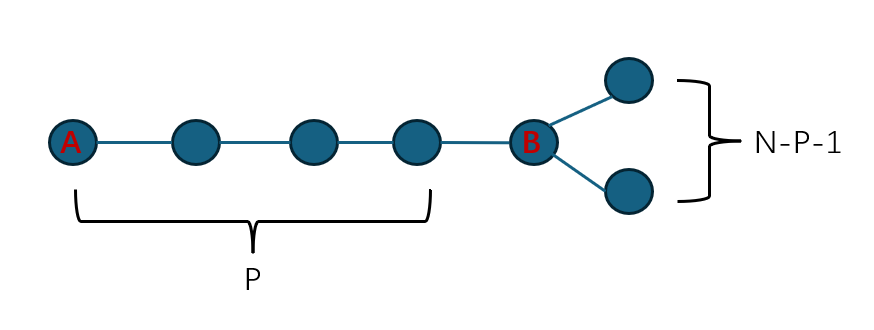
 不妨设A到B的路径上共经过了P个点，则B的子树里有N-P-1个点，对f(A)-f(B)能产生的贡献一共是P*(N-P-1)

根据均值不等式，和一定时两数乘积要最大，必然要两数尽量相等，即P=N-P-1，P=(N-1)/2

当N-1=2k时，也就是N为奇数时，P值即为k

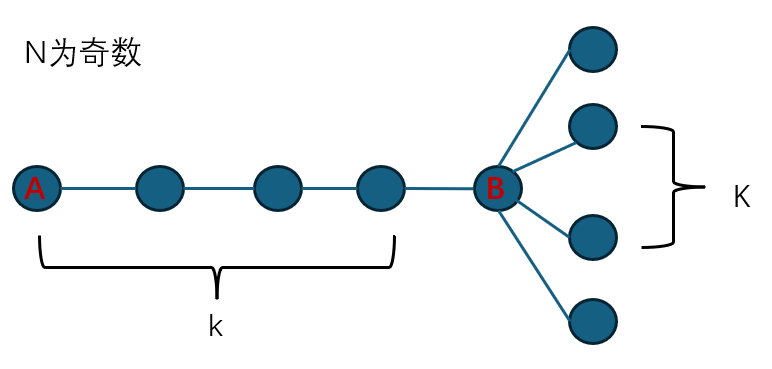
f(A)-f(B)取到极值K*K

当N-1=2k+1时，也就是N为偶数时，P值为k+1，B子树里有k个

 

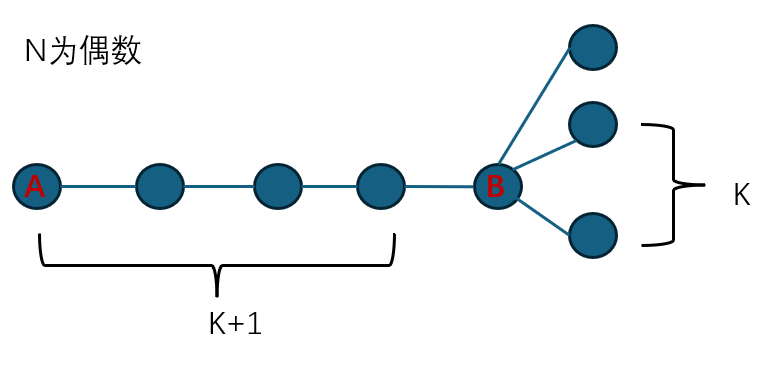
f(A)-f(B)取到极值(K+1)*K

至此我们有结论一：

输入为K^2时，答案为2K+1，输入为K*(K+1)时，答案为2K+2，输入为(K+1)*(K+1)时，答案为2(K+1)+1=2K+3

而在这之间，由于答案具有单调性，且每个点我们都取到了最大值，[K*K+1,K*K+K-1]肯定是比2K+1大的

 现在到了最麻烦的部分，证明：

① 在输入为[K*K+K+1，(K+1)^2)时，证明2K+3能覆盖到所有值

先考虑取到K*K+K，只要在原来K*K的基础上在B的子树里再接一个点就能+K

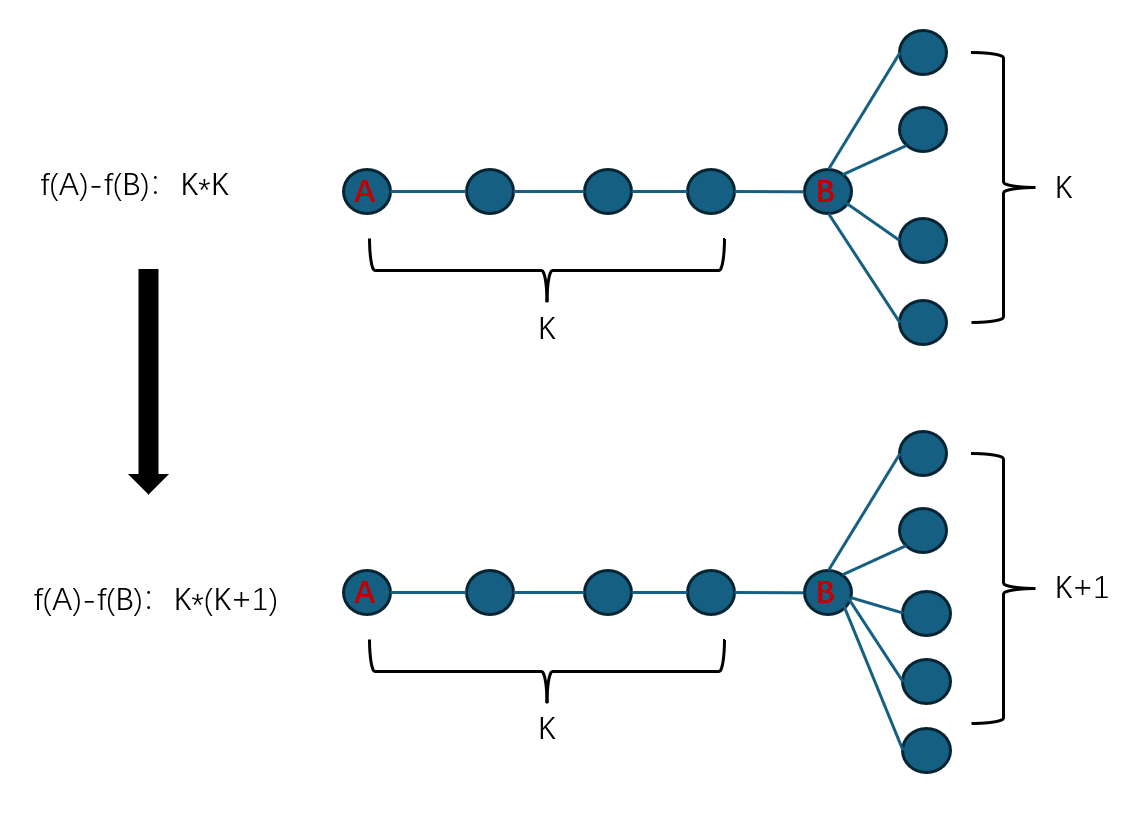
接下来的事情就有趣了

首先怎么整+1？

发现如果A到B（不包含B）的个数为奇数的话，只要取中间且尽量靠B的点就能+1

因为奇数总是可以拆成k+1,k的和的形式，只要让A得到的贡献是k+1，必然比B多1

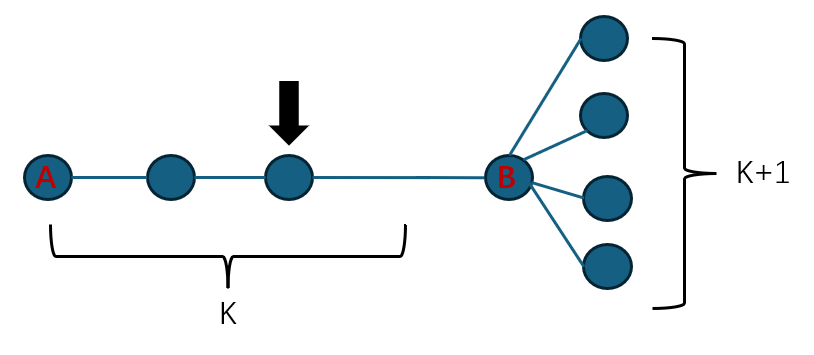
那怎么整+3？

发现在链上加点能+1，+3，+5...

这样就在原来2K+1的基础上再加两个点(一个在子树内，一个在路径上)得到了[K*K+K+1，(K+1)^2)里一半的值，下图是k=5时的例子

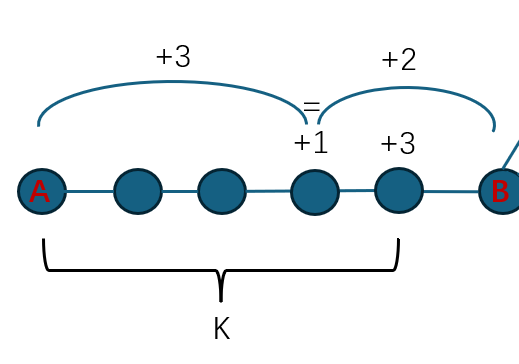
那怎么整+2?

发现如果最开始凑K的那个点一直留在B的子树内的话，怎么加都是1，3，5，没法得到2，4，6

这是因为在AB路径上每多走一条边，对A是+1，对B是-1，贡献的变化肯定是偶数

所以我们发挥人类智慧把这个点拉到链上，这也是让贡献+K

 

 

 

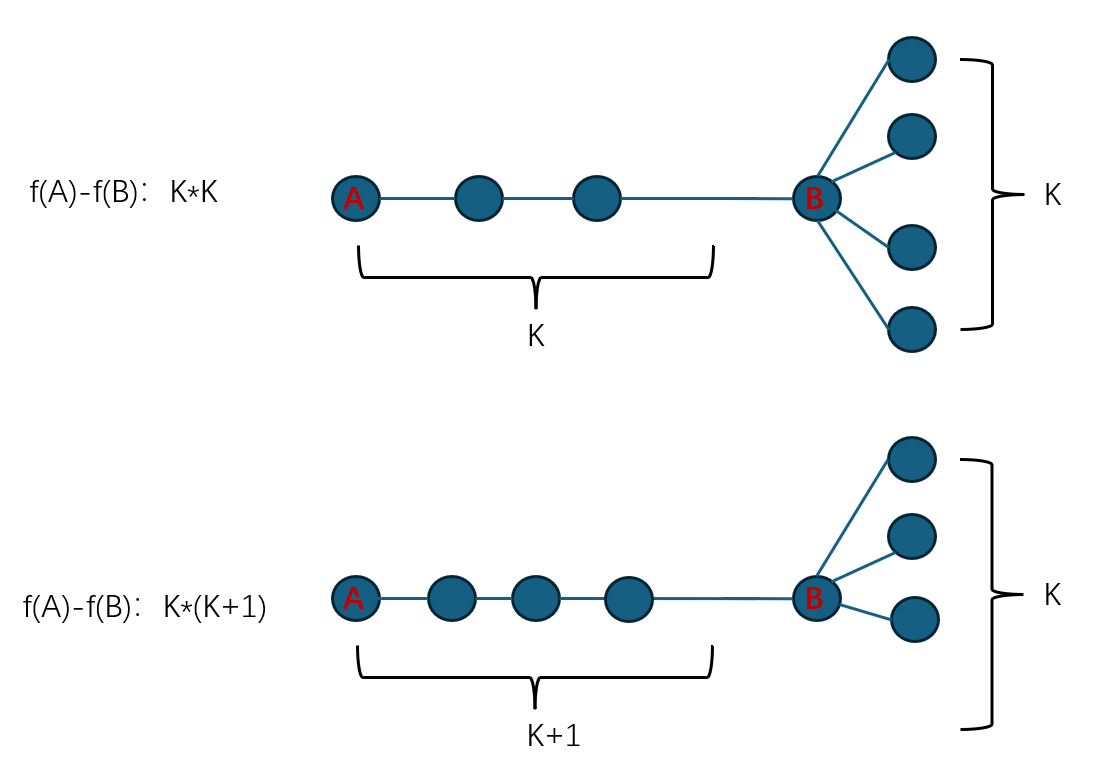
发现取中间加点贡献为0，往右边挪一个贡献+2，再往右一个+4...

这样就取到了另外一半的值。

当k=偶数时同理，至此我们证明了当输入在[K*K+K+1，(K+1)^2)，2k+3能覆盖所有值。

②那么用2k+2能否取遍[K*K+1，K*K+K) ？

这次因为不需要先凑出K，我们先只考虑多出来的一个点放哪。

当K为奇数时，根据上面的推理，从中间往B加依次能得到+1，+3，...的贡献

当K为偶数时，依次能得到+2，+4，...的贡献

也就是说如果x-K*K(这里x是输入的)和K同余的话，一定能只用一个点凑到。

 如果不同余呢？

这时只加一个点无论如何是不够的，不管怎么调整（加在子树上无解，路上上无解，调整子树大小还会变小），一定至少需要2个点。

现在证明2个点一定能凑出来：

如果K是奇数：原本加一个点只能+1，+3，多了一个点后+2可以通过在+1的地方加两个点，用1+1凑，4可以用1和3凑，6可以用1和5凑...

如果K是偶数：原本只能+2，+1怎么凑？先把子树中的一个点拎到链上，答案就从K*K变成(K+1)*(K-1)=K*K-1

接下来手上有两个点了，能凑出1+1=2，1+3=4......加上K*K-1就能依次得到K*K+1，K*K+3......

至此我们证完了结论②。

整理一下结论：

附上队友写的代码：

#include<cstdio>
#include<iostream>
#include<cmath>
#define int long long
using namespace std;
int T,x;
int sol(){
    cin >> x;
    int n=sqrt(x);
    while (n*n>x) n--; 
    //printf("n=%lld\n",n);
    if (n*n==x) return 2*n+1;
    if (n*n+n>=x){
        if ((n*n+n-x)%2) return 2*n+3;
        return 2*n+2;
    }
    else{
        return 2*n+3;
    }
}
void test(){
    for (int i=1;i<=10;i++){
        x=i;
        printf("%lld:%lld\n",i,sol());
    }
}
signed main(){
//    test();
    cin >> T;
    while(T--) cout << sol() << endl;
    return 0;
}