每天一道蓝桥杯Day1 分考场(dfs+结论)

题意：

这道题第一眼咋看以为是图论，但是要抽象成图论的话就会变成：

给定一个无向图，要求对点染色，使得任意相邻点之间颜色不能相同，试问最少的颜色数是多少？

发现转化成图论后好像也没有什么图论算法可以解决，这个转化不是很有效。

往往不知道怎么下手时可以试着考虑极端情况，比如考虑上界/下界，答案很小会怎么样，很大会怎么样

假设现在有n个人，最少考场数是我们要求的，最多考场数呢？

n个人n个考场肯定够用，但是n个肯定太多了。

n=3时

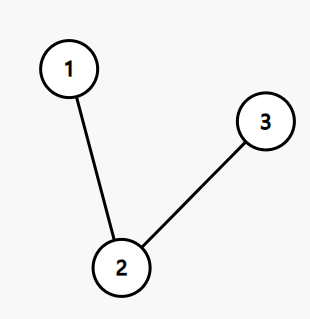
这种情况只需要2个   

 

这种情况需要3个

n=4时

需要3个 

 需要3个

需要4个。

有一个直观的直觉：图越密，需要的考场数越多。

最密的图是完全图，也就是说n个点的图，如果需要n个考场，那么就需要n*(n-1)/2条边，而此题m<=n

我们隐约感觉到，这个上界远远达不到n，应该会小于sqrt(n)？（不会证明2333）

数据不大，就可以考虑搜索

依次遍历每个人，判断当前她能放进哪个考场，能放则放，继续搜索；还有一种情况是给此人单独开一个考场

code：

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=105;
vector<int>e[N];
int ans=INT_MAX;
int at[N];
void dfs(int step,int k){
    if(k>=ans) return;//剪枝
    //如果当前用到的考场已经大于曾经找出来的最优解，则必然不会是最优解
    if(step==n+1){
        ans=min(ans,k);
        return;
    }
    for(int i=1;i<=k;i++){
        int flag=1;
        //判断是否会冲突
        for(auto v:e[step]){
            if(at[v]==i) flag=0;
        }
        if(!flag) continue;
        at[step]=i;
        dfs(step+1,k);
    }
    //单独开一个考场的情况
    at[step]=k+1;
    dfs(step+1,k+1);
}
int main(){
    
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int a,b;cin>>a>>b;
        e[a].push_back(b);
        e[b].push_back(a);
    }
    dfs(1,0);
    cout<<ans<<endl;
}

题外话：

1.这个问题其实有背景，是很著名的图着色问题，并且是个NP问题，没有多项式解法。

2.蓝桥杯好多搜索题，不会就暴力！

3.这道题的数据出题人应该没有造的很强。刚才写了个随机数生成数据，造了一组n=100，m=100的，ac代码跑了整整好几分钟

4.有一道类似的题(https://vjudge.net.cn/problem/%E6%B4%9B%E8%B0%B7-P5194)，也是表面数据很大，分析完发现其实情况有限，可以搜索解决。