Codeforces Round 932 (Div. 2)A-D

A. Entertainment in MAC

这道没细看题意，挺困的，猜了一下..

观察到n是偶数且很大，但是样例的长度却没有很长。

而且长度越长对字典序容易越大，所以猜测只复制一次。

从样例找规律：如果字符串s比翻转后的字符串s'小，则原样输出；否则进行翻转，再复制一次。

代码：

#include<bits/stdc++.h>
using namespace std;
void solve(){
    int n;
    cin>>n;
    string s;cin>>s;
    string b=s;
    reverse(b.begin(),b.end());
    if(b<s) cout<<b+s<<endl;
    else cout<<s<<endl;
}
int main(){
    int t;
    cin>>t;
    while(t--){
        solve();
    }
}

B.Informatics in MAC

题意：问是否能把一个数组划分成k段，使得每段的mex值一样。

出现mex这种特殊的值自然可以猜一猜性质。

假设每段的mex都==d，则:

1.d不能在数组中出现

2.[0,d-1]都必须在数组中出现

综合以上两点可以推出d必然是原数组的mex。

那么只要o(N)扫一遍，检查当前是否凑齐了[0,d-1]，没有凑齐继续凑；凑齐了则得到一个新的合法段。

最后如果能完整凑出来的段数<2，输出-1；

否则对于最后一段如果不能覆盖到n的话特殊处理一下即可

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int a[N];
void solve(){
    int n;
    cin>>n;
    map<int,int>mp;
    for(int i=1;i<=n;i++) cin>>a[i],mp[a[i]]=1;
    int mex=0;
    for(int i=0;i<=n;i++){
        if(!mp[i]) {
            mex=i;break;
        }
    }
    vector<pair<int,int>>ans;
    mp.clear();
    int cnt=0,lastl=1;
    for(int i=1;i<=n;i++){
        if(a[i]<mex){
            if(!mp[a[i]]) {
                mp[a[i]]=1;
                cnt++;
            }
        }
        if(cnt==mex){
           // cout<<lastl<<" "<<i<<endl;
            ans.push_back({lastl,i});
            lastl=i+1;
            cnt=0;
            mp.clear();
        }
    }
    if(ans.size()<2) {
        cout<<-1<<endl;return;
    }
    int id=ans.size();
    cout<<id<<endl;
    for(int i=0;i<=id-2;i++) cout<<ans[i].first<<" "<<ans[i].second<<endl;
    if(ans[id-1].second!=n){
        cout<<ans[id-1].first<<" "<<n<<endl;
    }
    else cout<<ans[id-1].first<<" "<<ans[id-1].second<<endl;
}
int main(){
    int t;
    cin>>t;
    while(t--){
        solve();
    }
}

　　

C.Messenger in MAC

这道题n的范围<=2000，很容易想到o(n^2)的dp或者枚举答案什么的。

cf很多c题如果是这个范围都可以往这边想。

首先发现一个性质：

对bi从小到大排序是最优的。

假设挑选出来的bi不是从小到大减的，也就是说不满足b1<=b2<=b3<=b4，

那一定会出现这种情况：

发现排完序后不会变差

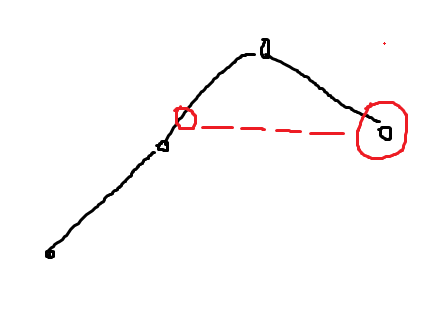
 反而可能变优

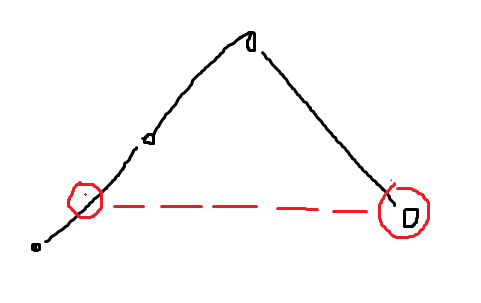
所以考虑对bi从小到大排序。

设dp[i][j]表示强制选第i个，一共选了j个的最小花费，寻找答案时只要找到最大的 j 使得dp[_][j]<=L即可。

转移：

最容易想到O(n^3)暴力，for i/j/k 三层循环下去，时间复杂度不能接受。

 for(int i=1;i<=n;i++){
        dp[i][1]=f[i].a;
        for(int j=2;j<=i;j++){
            for(int k=1;k<i;k++)
            if(j-1<=k) {
                dp[i][j]=min(dp[k][j-1]+f[i].a+f[i].b-f[k].b,dp[i][j]);
              //  cout<<i<<" "<<j<<" :"<<dp[i][j]<<endl;
            }
        }
    }

发现时间主要浪费在枚举i是从哪个k转移过来的，考虑优化。

观察到转移方程可以写作dp[k][j-1]-f[k].b + (f[i].a+f[i].b)，括号里的数为定值

则只需要对于每一个j-1，维护最小的 dp[k][j-1]-f[k].b，转移时直接拿出来更新即可。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e3+5;
#define int long long
struct node{
    int a,b;
}f[N];
int dp[N][N],s[N];
bool cmp(node x,node y){
    if(x.b==y.b) return x.a<y.a;
    else return x.b<y.b;
}
void solve(){
    int n,l;cin>>n>>l;
    for(int i=1;i<=n;i++)  cin>>f[i].a>>f[i].b;
    sort(f+1,f+n+1,cmp);

    int ans=-1;
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
        dp[i][j]=1e15,s[j]=1e15;
        
    for(int i=1;i<=n;i++){

        dp[i][1]=f[i].a;
        for(int j=i;j>=2;j--){
            dp[i][j]=min(dp[i][j],s[j-1]+f[i].a+f[i].b);
            s[j]=min(s[j],dp[i][j]-f[i].b);
            /*
            for(int k=1;k<i;k++)
            if(j-1<=k) {
                dp[i][j]=min(dp[k][j-1]+f[i].a+f[i].b-f[k].b,dp[i][j]);
            }
            */
           //cout<<i<<" "<<j<<" # "<<dp[i][j]<<" "<<s[j-1]<<" "<<endl;
        }
        s[1]=min(s[1],dp[i][1]-f[i].b);
    }
     
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++){
          //  cout<<i<<" "<<j<<" # "<<dp[i][j]<<endl;
            if(dp[i][j]<=l) ans=max(ans,j);
        }
    cout<<max(ans,1ll*0)<<endl;
}
signed main(){
    int t;
    cin>>t;
    while(t--){
        solve();
    }
}

D.Exam in MAC

这道d最后过得比c还多..但是有点久没写代码，c调太久了，d没过掉。

题意：给定c和集合s，求x+y不在集合s出现过，y-x(y>=x)也不在集合s出现过的(x,y)对数

如果要正解求解发现由于c的值域很大，如果要枚举x做不到，好像也没其他好办法

考虑正难则反

如果从[1,c]中任取两个数，方案是C(n,2)

那么只要减去x+y在集合中，y-x在集合中，根据容斥原理，再加上x+y且y-x都在集合中的情况。

一一讨论。

1.y-x在集合中

若y-x=s[i]，移项，s[i]+x=y

对x和y的限制只有 x、y<=c，显然此时x取[1,c-s[i]]都是合法的，且x和y都是一一对应的

这样的x个数是c-s[i]+1。

2.x+y在集合中

若x+y=s[i]，则s[i]可以等于1+si-1,2+si-2...，共有s[i]/2对

3.x+y在集合中且y-x在集合中

假设x+y=s[i]，y-x=s[j]

则y=(s[i]+s[j])/2,x=(s[i]-s[j])/2

为了能被2整除，s[i]和s[j]的奇偶性一定要相同，此外没有其他限制

这部分的贡献就是C(cnt_0,2)+C(cnt_1,2)，其中cnt_0为s[i]%2==0的个数。

AC代码：

//搬了一个房间别人的

#include<bits/stdc++.h>
#include<set>
#include<queue>
#include<stack>
#include<algorithm>
 
using namespace std;
using ll = long long;
const int NMAX = 3e5;
const ll MOD = 1e9 + 7;
const ll INF = 1e18 + 4;
 
int s[NMAX+5];
 
int main ()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
 
    
    int q; cin >> q;
    while (q--)
    {
        int n, c; cin >> n >> c;
        int count[2] = {0,0};
        for (int i = 1; i <= n; i++)
        {
            cin >> s[i];
            count[s[i]&1]++;
        }
        
        ll ans = 1ll * (c+1) * (c+2)/2;
 
        for (int i = 1; i <= n; i++)
        {
            ans -= s[i]/2;
            ans -= c - s[i] + 1;
        }
 
        ans += 1ll * count[0] * (count[0]-1) / 2;
        ans += 1ll * count[1] * (count[1]-1) / 2;
 
        count[0] = count[1] = 0;
 
        cout << ans << '\n';
    }
    
    
}