Codeforces Round 921 (Div. 2) A-D
倒叙讲题预警()
传送门:https://codeforces.com/contest/1925
D.Good Trip
题意:有n个小盆友,其中m对是好盆友,每队好盆友有友谊度fi。老师要举办k次远足,每次挑一对小盆友去,被挑到的小盆友友谊值+1。如果一对儿童不是朋友,那么他们的友谊值为0,在以后的游览中不会改变。求所有被选中参加远足的 k 对的友谊值总和的期望值(在被选中时)。
分析:
首先友谊值为0的小盆友队不会产生任何贡献,我们只关心m对好盆友。
如果要把f作为一个整体去看,还要考虑每队被挑选了多少次,虽然增长值好算,但是基础值是不一样的。但是如果把f拆成基础的部分和增长的部分,并且若基础的部分可以先算,那增长的部分是很平等的。
可以这么拆分的依据是期望的线性。

接下来考虑增长部分怎么算?问题转化成有k次分配机会,共有 n * (n-1)/2个对象可以分配,当且仅当分配到m对好盆友会有贡献。同一好盆友被分配到第一次贡献是0,第二次贡献是1,第三次贡献是2...观察到这时m对好盆友的地位都是“平等”的,也就是说我们可以只算一个的期望,然后*m。而对于每个个体来说都是独立的,所以就变成了简单的概率论。
一对小盆友的期望为:
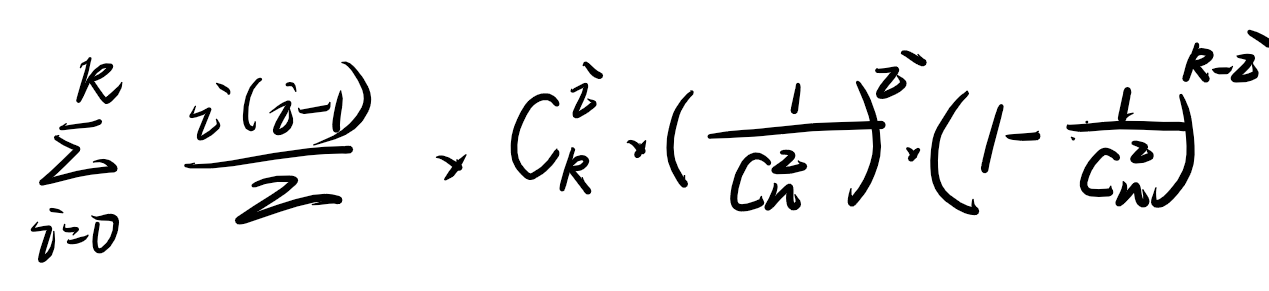
然后*m即可。
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=1e9+7;
const int N=1e6+5;
int power(int a, int b, int p=mod)
{
if(b==0)
return 1;
if(a==0)
return 0;
int res=1;
a%=p;
while(b>0)
{
if(b&1)
res=(1ll*res*a)%p;
b>>=1;
a=(1ll*a*a)%p;
}
return res;
}
int fact[N],inv[N];
void pre()
{
fact[0]=1;
inv[0]=1;
for(int i=1;i<N;i++)
fact[i]=(i*fact[i-1])%mod;
for(int i=1;i<N;i++)
inv[i]=power(fact[i], mod-2, mod);
}
int nCr(int n, int r, int p=mod)
{
if(r>n || r<0)
return 0;
if(n==r)
return 1;
if (r==0)
return 1;
return (((fact[n]*inv[r]) % p )*inv[n-r])%p;
}
void solve(){
int n,m,k;
cin>>n>>m>>k;
int sum=0,mm=m;
while(mm--){
int a,b,f;cin>>a>>b>>f;
sum=(sum+f)%mod;
}
int base=nCr(n,2);
base=power(base,mod-2)*sum%mod*k%mod;
int div=0;
int chose=power((n*(n-1)/2ll)%mod,mod-2)%mod;
for(int i=1;i<=k;i++){
int sum=(i*(i-1)/2)%mod;
int prob=nCr(k,i)*power(chose,i)%mod;
int un_prob=((n*(n-1)/2ll)%mod-1+mod)%mod*chose%mod;
un_prob=power(un_prob,k-i);
prob=prob*un_prob%mod;
sum=sum*prob%mod;
div=(div+sum)%mod;
}
div=div*m%mod;
cout<<(base+div)%mod<<endl;
}
signed main( ){
pre();
int t;
cin>>t;
while(t--){
solve();
}
}
C
解析:
考虑什么情况下满足条件?
在字符集大小为k的前提下,既然要求所有长度为n的串都要出现,参考A题,显然可以构造出abc/abc/abc这样的形式,进一步地我们发现每段abc内顺序是不重要的,所以abc/cba/acb也是可行的。
再进一步地,给我们的字符串不会这么美观,可能是aaacbbbbcaaaa的形式,但本质上是一样的,如果要合法的话,我们希望让前k个字符集都出现一遍,作为一个block,如此循环直到字符串结束。为什么要让前k个字符都出现一遍?这样最不会有漏洞,否则就可以根据没出现的那个字符构造反例。
根据上述思想,可以把aaacbbbbcaaaa划分为aaacb/bbbca/aaa,发现abc完整的出现只能出现两段,如果此时n=3的话,那显然无解。因为可以取每个block最后一次才出现的字符拼接起来(第一段blcok是aaacb,最后一次出现是b;第二段block是bbbca,最后一次出现是a),然后加上没出现过的字符(第三段是不完整的block,只出现了a,b和c都没出现过)作为答案。则bab或者bac都是可行的反例。
注意:这里取每个block的最后一个字符是一种贪心思想,显然取完一个字符后往后挪得越远越好,这样最容易无解。否则随机取的话,可能前面block里会有字母重复,很快就找到符合条件的序列了。
代码
#include<bits/stdc++.h>
using namespace std;
void solve(){
int n,k,m;
cin>>n>>k>>m;
string s;cin>>s;
int vis[30]={0},cnt=0;
memset(vis,0,sizeof(vis));
int block=0;
string ans="";
vector<char>e;
for(int i=0;i<m;i++){
int id=s[i]-'a';
if(vis[id]) continue;
vis[id]=1;
cnt++;
if(cnt==k) {
cnt=0;
e.push_back(s[i]);
memset(vis,0,sizeof(vis));
block++;
}
}
if(block>=n) {
cout<<"YES"<<endl;
}
else {
cout<<"NO"<<endl;
for(int i=0;i<block;i++) cout<<e[i];
//有不完整的
for(int i=0;i<k;i++){
if(vis[i]==0){
for(int h=0;h<n-block;h++)
cout<<(char)(97+i);
cout<<endl;
return;
}
}
//全做完的,但是长度不够,随便输出a
for(int h=0;h<n-block;h++)
cout<<(char)(97);
cout<<endl;
return;
}
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
}
B
解析:
刚开始看咋可能有点吓人,要求n个数和为x,且它们的gcd最大。但是写到纸面上来后,一个很常见的技巧是设gcd(x1,x2,x3...xn)=g,然后反过来把x1表达为g * k1,x2表达为g * k2,这样就转化成:
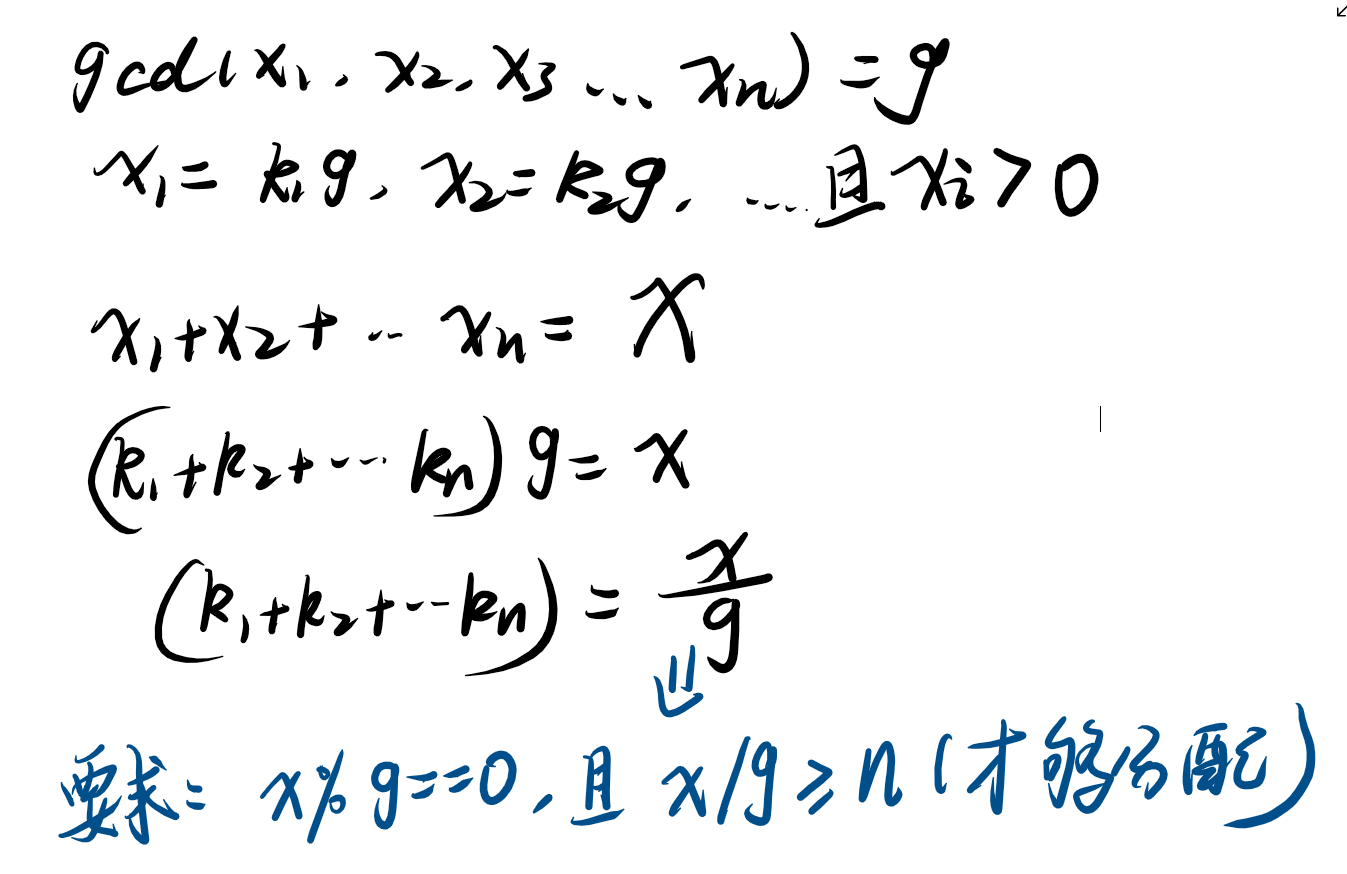
则直接sqrt(x)地去分解x,判断能否整除,更新答案。
代码:
#include<bits/stdc++.h>
using namespace std;
void solve(){
int x,n;
cin>>x>>n;
int up=sqrt(x)+1;
int ans=1;
for(int i=1;i<=up;i++){
if(x%i==0){
int j=x/i;
if(i>=n) ans=max(ans,j);
if(j>=n) ans=max(ans,i);
}
}
cout<<ans<<endl;
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
}
A
解析:
显然构造诸如abc/abc的形式即可
代码:
#include<bits/stdc++.h>
using namespace std;
void solve(){
int n,k;
cin>>n>>k;
for(int i=1;i<=n;i++){
for(int j=1;j<=k;j++) cout<< char(97+j-1);
}
cout<<endl;
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号