hdu 2215 & hdu 3932(最小覆盖圆)
Maple trees
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1847 Accepted Submission(s): 574
Problem Description
There are a lot of trees in HDU. Kiki want to surround all the trees with the minimal required length of the rope . As follow,
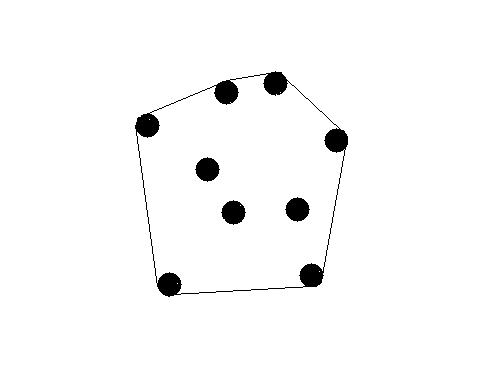
To make this problem more simple, consider all the trees are circles in a plate. The diameter of all the trees are the same (the diameter of a tree is 1 unit). Kiki can calculate the minimal length of the rope , because it's so easy for this smart girl.
But we don't have a rope to surround the trees. Instead, we only have some circle rings of different radius. Now I want to know the minimal required radius of the circle ring. And I don't want to ask her this problem, because she is busy preparing for the examination.
As a smart ACMer, can you help me ?
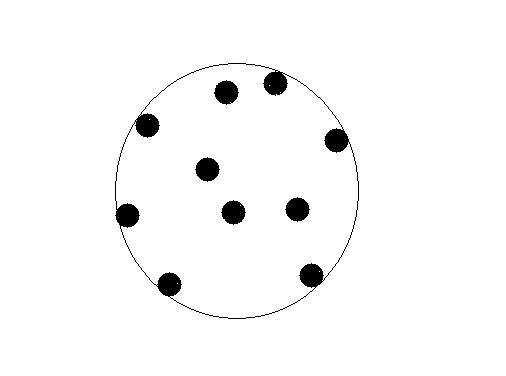

To make this problem more simple, consider all the trees are circles in a plate. The diameter of all the trees are the same (the diameter of a tree is 1 unit). Kiki can calculate the minimal length of the rope , because it's so easy for this smart girl.
But we don't have a rope to surround the trees. Instead, we only have some circle rings of different radius. Now I want to know the minimal required radius of the circle ring. And I don't want to ask her this problem, because she is busy preparing for the examination.
As a smart ACMer, can you help me ?

Input
The
input contains one or more data sets. At first line of each input data
set is number of trees in this data set n (1 <= n <= 100), it is
followed by n coordinates of the trees. Each coordinate is a pair of
integers, and each integer is in [-1000, 1000], it means the position of
a tree’s center. Each pair is separated by blank.
Zero at line for number of trees terminates the input for your program.
Zero at line for number of trees terminates the input for your program.
Output
Minimal required radius of the circle ring I have to choose. The precision should be 10^-2.
Sample Input
2
1 0
-1 0
0
Sample Output
1.50
最小圆覆盖问题:
一.概念引入
最小包围圆问题:对于给定的平面上甩个点所组成的一个集合P,求出P的最小包围圆,即包含P中所有点、半径最小
的那个圆。也就是求出这个最小包围圆的圆心位置和半径。
下面是若干性质。
1.有限点集P的最小包围圆是唯一的。这里约定,若P中只有一个点v,则最小包围圆是退化的,其半径为0,圆心为点v。
2.非退化最小包围圆可以由2个或者3个边界点定义。边界上只有两个点,则必定是直径两端,其它点都在圆内部。
3.点集P中,距离最大的2个点A、B不一定都在边界上,但是必有d≥|AB|。
4.直角三角形或钝角三角形的3个顶点的最小包围圆是以最长边为直径的圆;锐角三角形3个顶点的最小包围圆是三角形
的外接圆。
5.新加入点一定在圆上。
以上资料参考:http://www.cnblogs.com/hxsyl/p/3226562.html
hdu 2215
///最小圆覆盖问题: /**一.概念引入 最小包围圆问题:对于给定的平面上甩个点所组成的一个集合P,求出P的最小包围圆,即包含P中所有点、半径最小 的那个圆。也就是求出这个最小包围圆的圆心位置和半径。 下面是若干性质。 1.有限点集P的最小包围圆是唯一的。这里约定,若P中只有一个点v,则最小包围圆是退化的,其半径为0,圆心为点v。 2.非退化最小包围圆可以由2个或者3个边界点定义。边界上只有两个点,则必定是直径两端,其它点都在圆内部。 3.点集P中,距离最大的2个点A、B不一定都在边界上,但是必有d≥|AB|。 4.直角三角形或钝角三角形的3个顶点的最小包围圆是以最长边为直径的圆;锐角三角形3个顶点的最小包围圆是三角形 的外接圆。 5.新加入点一定在圆上。 */ #include <iostream> #include <cstdio> #include <string.h> #include <math.h> #include <algorithm> using namespace std; const int N = 105; const double eps = 1e-8; struct Point{ double x,y; }p[N]; Point c; ///这是最小圆的圆心 double r; ///这是最小圆半径 int n; double dis(Point a,Point b){ return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); } /**计算外接圆的圆心*/ Point circumcenter(Point a,Point b,Point c){ Point ret=a; double a1 = (b.x-a.x),b1=(b.y-a.y),c1 = (a1*a1+b1*b1)/2; double a2 = (c.x-a.x),b2=(c.y-a.y),c2 = (a2*a2+b2*b2)/2; double d=a1*b2-a2*b1; ret.x+=(c1*b2-c2*b1)/d; ret.y+=(a1*c2-a2*c1)/d; return ret; } void min_cover_circle(){ //random_shuffle(p,p+n); ///模板上面的这个函数是打乱点,这个题不要比要还快15MS c = p[0],r = 0; for(int i=1;i<n;i++){ ///i是第一个点 if(dis(p[i],c)-r>eps){ c = p[i],r=0; for(int j=0;j<i;j++){ ///j是第二个点 if(dis(p[j],c)-r>eps){ c.x = (p[i].x+p[j].x)/2; c.y = (p[i].y+p[j].y)/2; r = dis(p[j],c); for(int k=0;k<j;k++){ ///k是第三个点 if(dis(p[k],c)-r>eps){ c = circumcenter(p[i],p[j],p[k]); r = dis(p[i],c); } } } } } } } int main() { while(scanf("%d",&n)!=EOF&&n){ for(int i=0;i<n;i++){ scanf("%lf%lf",&p[i].x,&p[i].y); } min_cover_circle(); printf("%.2lf\n",r+0.5); } return 0; }
hdu 3932
///最小圆覆盖问题: /**一.概念引入 最小包围圆问题:对于给定的平面上甩个点所组成的一个集合P,求出P的最小包围圆,即包含P中所有点、半径最小 的那个圆。也就是求出这个最小包围圆的圆心位置和半径。 下面是若干性质。 1.有限点集P的最小包围圆是唯一的。这里约定,若P中只有一个点v,则最小包围圆是退化的,其半径为0,圆心为点v。 2.非退化最小包围圆可以由2个或者3个边界点定义。边界上只有两个点,则必定是直径两端,其它点都在圆内部。 3.点集P中,距离最大的2个点A、B不一定都在边界上,但是必有d≥|AB|。 4.直角三角形或钝角三角形的3个顶点的最小包围圆是以最长边为直径的圆;锐角三角形3个顶点的最小包围圆是三角形 的外接圆。 5.新加入点一定在圆上。 */ #include <iostream> #include <cstdio> #include <string.h> #include <math.h> #include <algorithm> using namespace std; const int N = 1005; const double eps = 1e-8; struct Point{ double x,y; }p[N]; Point c; ///这是最小圆的圆心 double r; ///这是最小圆半径 int n; double dis(Point a,Point b){ return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); } /**计算外接圆的圆心*/ Point circumcenter(Point a,Point b,Point c){ Point ret=a; double a1 = (b.x-a.x),b1=(b.y-a.y),c1 = (a1*a1+b1*b1)/2; double a2 = (c.x-a.x),b2=(c.y-a.y),c2 = (a2*a2+b2*b2)/2; double d=a1*b2-a2*b1; ret.x+=(c1*b2-c2*b1)/d; ret.y+=(a1*c2-a2*c1)/d; return ret; } void min_cover_circle(){ //random_shuffle(p,p+n); ///模板上面的这个函数是打乱点,这个题不要比要还快15MS c = p[0],r = 0; for(int i=1;i<n;i++){ ///i是第一个点 if(dis(p[i],c)-r>eps){ c = p[i],r=0; for(int j=0;j<i;j++){ ///j是第二个点 if(dis(p[j],c)-r>eps){ c.x = (p[i].x+p[j].x)/2; c.y = (p[i].y+p[j].y)/2; r = dis(p[j],c); for(int k=0;k<j;k++){ ///k是第三个点 if(dis(p[k],c)-r>eps){ c = circumcenter(p[i],p[j],p[k]); r = dis(p[i],c); } } } } } } } int main() { int X,Y; while(scanf("%d%d%d",&X,&Y,&n)!=EOF){ for(int i=0;i<n;i++){ scanf("%lf%lf",&p[i].x,&p[i].y); } min_cover_circle(); printf("(%.1lf,%.1lf).\n%.1lf\n",c.x,c.y,r); } return 0; }



