poj 1654(利用叉积求面积)

Area

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 17937		Accepted: 4957

Description

You are going to compute the area of a special kind of polygon. One vertex of the polygon is the origin of the orthogonal coordinate system. From this vertex, you may go step by step to the following vertexes of the polygon until back to the initial vertex. For each step you may go North, West, South or East with step length of 1 unit, or go Northwest, Northeast, Southwest or Southeast with step length of square root of 2.

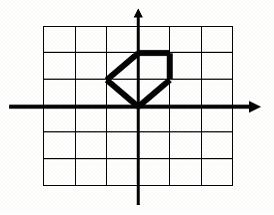
For example, this is a legal polygon to be computed and its area is 2.5:

Input

The first line of input is an integer t (1 <= t <= 20), the number of the test polygons. Each of the following lines contains a string composed of digits 1-9 describing how the polygon is formed by walking from the origin. Here 8, 2, 6 and 4 represent North, South, East and West, while 9, 7, 3 and 1 denote Northeast, Northwest, Southeast and Southwest respectively. Number 5 only appears at the end of the sequence indicating the stop of walking. You may assume that the input polygon is valid which means that the endpoint is always the start point and the sides of the polygon are not cross to each other.Each line may contain up to 1000000 digits.

Output

For each polygon, print its area on a single line.

Sample Input

4
5
825
6725
6244865

Sample Output

0
0
0.5
2

题意:输入一个长为n字符串,前n-1个字符分别为1-4,6-9中的某个数字,最后一个数字5代表输入的结束,除了5以外
每个点都代表了一个方向,问这些点组成的面积是多少？？
分析：设从(0,0)出发,然后将每个点记录下来,然后利用叉积求解多边形面积。（这里要用滚动数组优化）
最重要的一点是一定一定要记得用long long 不能用double 我是被坑到死。。。

///题意:输入一个长为n字符串,前n-1个字符分别为1-4,6-9中的某个数字,最后一个数字5代表输入的结束,除了5以外
///每个点都代表了一个方向,问这些点组成的面积是多少？？
///分析：设从(0,0)出发,然后将每个点记录下来,然后利用叉积求解多边形面积。
#include<stdio.h>
#include<iostream>
#include<string.h>
#include <stdlib.h>
#include<math.h>
#include<algorithm>
using namespace std;
const int N = 1000005;
const double esp = 1e-8;
struct Point{
    long long x,y;
}p[3];

long long mult(Point a,Point b){
    return (a.x*b.y-a.y*b.x);
}
char str[N];
int dir[10][2]={{0,0},{-1,-1},{0,-1},{1,-1},{-1,0},{0,0},{1,0},{-1,1},{0,1},{1,1}};
int main()
{
    int tcase;
    scanf("%d",&tcase);
    while(tcase--){
        scanf("%s",str+1);
        int len = strlen(str+1);
        if(len==1) {printf("0\n");continue;}
        p[1].x = dir[str[1]-'0'][0];
        p[1].y = dir[str[1]-'0'][1];
        long long area = 0;
        for(int i=2;str[i]!='5';i++){
            p[i%2].x = dir[str[i]-'0'][0]+p[(i-1)%2].x;
            p[i%2].y = dir[str[i]-'0'][1]+p[(i-1)%2].y;
            area+=mult(p[i%2],p[(i-1)%2]);
        }
        //printf("%lf\n",area);
        if(area<0) area=-area;
        /*
        if(0.5-(area-(int)(area))<esp)
        printf("%.1lf\n",area);
        else printf("%.0lf\n",area);*/
        printf ("%I64d", area/2);
        if (area%2) printf (".5");
        printf ("\n");
    }
    return 0;
}