2020第十一届蓝桥杯软件类省赛第二场C/C++ 大学 B 组 E: 七段码(DFS,二进制枚举+并查集判重)
【问题描述】
小蓝要用七段码数码管来表示一种特殊的文字。
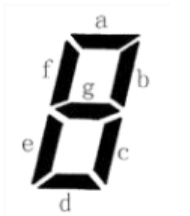
上图给出了七段码数码管的一个图示,数码管中一共有 7 段可以发光的二 极管,分别标记为 a, b, c, d, e, f, g。
小蓝要选择一部分二极管(至少要有一个)发光来表达字符。在设计字符 的表达时,要求所有发光的二极管是连成一片的。
例如: b 发光,其他二极管不发光可以用来表达一种字符。
例如: c 发光,其他二极管不发光可以用来表达一种字符。这种 方案与上 一行的方案可以用来表示不同的字符,尽管看上去比较相似。
例如: a, b, c, d, e 发光, f, g 不发光可以用来表达一种字符。
例如: b, f 发光,其他二极管不发光则不能用来表达一种字符,因为发光 的二极管没有连成一片。
请问,小蓝可以用七段码数码管表达多少种不同的字符?
答案:
80
1:
暴力数
dfs实现指数型枚举,然后自行根据是否连通一个一个数
#include<iostream> #include<cstring> #include<algorithm> #include<cmath> using namespace std; int n; int vis[20]; void dfs(int x) { if(x>n) { for(int i=1;i<=n;i++) if(vis[i]) cout<<i<<" "; cout<<endl; return ; } vis[x]=1; dfs(x+1); vis[x]=0; dfs(x+1); } int main() { cin>>n; // cout<<endl; dfs(1); return 0; }
2:
如果上面那个写不好,可能会出现重复情况。下面这个是自行map去重代码:
#include<iostream> #include<cstring> #include<map> #include<algorithm> #include<cmath> using namespace std; const int maxn=1e2+10; int vis[11]; int all=7; int cnt,sum=0; string s="0000000000"; map<string,int>mp; int dfs(int x) { if(x==cnt+1) { string s2; for(int i=1;i<=all;i++) s2+=s[i]; mp[s2]++; if(mp[s2]==1) {sum++; for(int i=1;i<=all;i++) if(s[i]!='0') cout<<s[i]; cout<<endl; } return 0; // cout<<sum<<endl; } for(int i=1;i<=all;i++) { if(s[i]=='0') { s[i]=i+'0'; dfs(x+1); s[i]='0'; } } } int getlcm(int a,int b) { return a*b/__gcd(a,b); } int main() { cnt=1;//cnt==1,2,3,4,5,6,7。自行更换值。 dfs(1); // cout<<sum<<endl; }
3:
二进制枚举+并查集判联通
1:首先说明:
(1):1<<7的意思是,把1左移七位。换成二进制就是:10000000
那么<(10000000)(二进制)的,就是0位~6位的所有情况。、
(2):第78行:if( i&(1<<j) )
假如 i 的二进制和 1<<2的二进制分别为:
1010100
0000100
如果if结果为真,说明i的第2位为1,即题目里的:发光
所以可以根据这个if,来枚举所有 i 二进制中为1的位置
2:并查集判联通。
这个就没得说了,根据图,一个一个连上就行。
每次判断vis[i]==1而且pr[i]==i的有几个,1个,就说明本次 i 的二进制只有一个连通块,符合要求,cnt++;
#include<iostream> #include<cstring> #include<algorithm> #include<cmath> using namespace std; const int maxn=1e2+10; int pr[11],vis[11]; void init(){memset(vis,0,sizeof(vis)); for(int i=0;i<=8;i++) pr[i]=i; } int find(int x){ if(x!=pr[x])return pr[x]=find(pr[x]); return x; } void add(int a,int b) { int fa=find(a),fb=find(b); if(fa!=fb) pr[fa]=fb; return ; } void check(int x) { vis[x]=1; if(x==0) { if(vis[1])add(0,1); if(vis[5])add(0,5); if(vis[6])add(0,6); } if(x==1) { if(vis[0])add(1,0); if(vis[6])add(1,6); if(vis[2])add(1,2); } if(x==2) { if(vis[1])add(2,1); if(vis[3])add(2,3); if(vis[6])add(2,6); } if(x==3) { if(vis[2])add(3,2); if(vis[4])add(3,4); } if(x==4) { if(vis[5])add(4,5); if(vis[6])add(4,6); if(vis[3])add(4,3); } if(x==5) { if(vis[0])add(5,0); if(vis[4])add(5,4); if(vis[6])add(5,6); } if(x==6) { if(vis[1])add(6,1); if(vis[2])add(6,2); if(vis[4])add(6,4); if(vis[5])add(6,5); } return ; } int main() { int cnt=0; for(int i=1;i<(1<<7);i++) //枚举所有排列 { init();//初始化 for(int j=0;j<=6;j++) { if(i&(1<<j))//1<<j的二进制表示,出现的第一个1与st中某个1同位置 { check(j);//加入连通 } } int ans=0; for(int j=0;j<=6;j++) { if(vis[j]&&pr[j]==j) ans++; } if(ans==1) cnt++; } cout<<cnt<<endl; return 0; }


