POJ--3321(dfs序树状转线性+树状数组+vector防超时写法)
地址:http://poj.org/problem?id=3321
题意:
树上有n个位置,初始每个位置都有苹果。以1号为总根
n-1条分叉边
m条询问:
Q:id 以id为根的子树有几个苹果
C:id id处如果有苹果,摘掉,否则放上一个苹果。
解析:
假设输入的是这么一棵树:
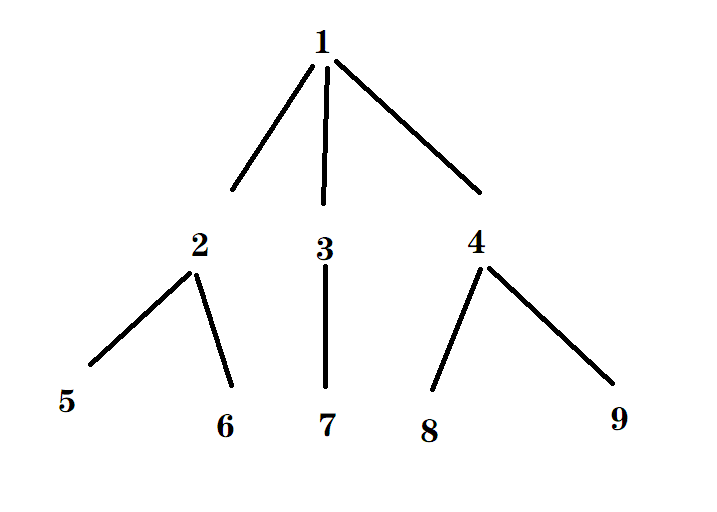
看数据,肯定要前缀和的思想,但是:
假设要询问4号为根的子树,我们要看的是4+8+9,这些序号很难通过前缀和来维护,因为输入的边并不是按顺序输的。
所以,考虑能不能把这些序号重新编排一下,使其能通过前缀和来求?
这里就引入了dfs序
st[],en[],来记录 i 在dfs序里的开始和结束位置
比如以此图为例:
dfs的遍历顺序:1 2 5 6 3 7 4 8 9
(st[i],en[i]): (1,9) (2,4) (3,3) (4,4) (5,6) (6,6) (7,9) (8,8) (9,9)
很好理解,结合树,比如4:(7,9)它在dfs序中以第7个开始,第9个结束。
所以有:
void dfs(int n) { num++; st[n]=num; for(int i=0;i<vv[n].size();i++) { dfs(vv[n][i]); } en[n]=num; }
剩下的就交给树状数组维护前缀和了,查询一个点,只需要:getsum(en[id])-getsum(st[id]-1)
vector防超时的写法:vector<vector<int> > vv(maxn);
总的代码:
#include <cstdio> #include<cstring> #include<map> #include<vector> #include<iostream> using namespace std; const int maxn =1e5+10; int st[maxn],en[maxn],vis[maxn],c[maxn]; vector<vector<int> > vv(maxn); int num=0; int lowbit(int x) { return x&(-x); } void update(int id,int x) { for(int i=id;i<maxn;i+=lowbit(i)) { c[i]+=x; } return ; } int getsum(int id) { int sum=0; for(int i=id;i>0;i-=lowbit(i)) sum+=c[i]; return sum; } void dfs(int n) { num++; st[n]=num; for(int i=0;i<vv[n].size();i++) { dfs(vv[n][i]); } en[n]=num; } int main() { int n; scanf("%d",&n); for(int i=1;i<=n-1;i++) { int a,b; scanf("%d%d",&a,&b); vv[a].push_back(b); } dfs(1); for(int i=1;i<=n;i++) { update(i,1); vis[i]=1; } int m; scanf("%d",&m); while(m--) { char ch[12]; scanf("%s",ch); if(ch[0]=='Q') { int id; scanf("%d",&id); cout<<getsum(en[id])-getsum(st[id]-1)<<endl; } else { int id; scanf("%d",&id); if(vis[id]) { vis[id]=0; update(st[id],-1); } else { vis[id]=1; update(st[id],1); } } } }
参考自:https://www.cnblogs.com/FrankChen831X/p/10800106.html 十分感谢!


