Codeforces Round #636 (Div. 3)


解析:把式子的x分出来,就是x*(2^0+2^1......+2^k-1)=n。所以先累加括号里的值打个表,只要n能整除它就输出
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> using namespace std; typedef long long ll; const int maxn=1e5+20; ll a[maxn]; int main() { ll n; int t; cin>>t; a[1]=1; ll sum = 1; for(int i=2;i<=1e9;i++) { sum*=2; a[i]=a[i-1]+sum; if(a[i]>=1e9) break; } while(t--) { cin>>n; for(int i=2;;i++) { if(n%a[i]==0) { cout<<n/a[i]<<endl;break; } } } }


题意:给出数组偶数长度n,能否输出一个:左边一半为偶数,右边一半为奇数,两边和相等。而且不存在重复数字。
解析:n/2的结果如果不是偶数,那么就肯定构造不出。比如6/2=3,奇数个奇数相加是奇数,是没办法等于偶数部分的和的。偶数部分直接按2,6,10构造,之间的差距不能为2,奇数部分直接参考左边对应位置,每次+1,-1即可,偶数差>2保证了奇数不会出现相等。
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> using namespace std; typedef long long ll; const int maxn=2e5+20; ll a[maxn]; ll b[maxn]; int main() { int t; cin>>t; while(t--) { int n; cin>>n; int md=n/2; if(md%2!=0) cout<<"NO"<<endl; else { cout<<"YES"<<endl; ll k=2,tot=0; ll sum=0; for(int i=1;i<=md;i++) { sum+=k; b[i]=k; k+=4; } int ok=0; for(int i=md+1;i<=n;i++) { if(!ok) { b[i]=b[i-md]-1; ok=1; } else { b[i]=b[i-md]+1; ok=0; } } for(int i=1;i<n;i++) cout<<b[i]<<" "; cout<<b[n]<<endl; } } }


题意:给出一组数,找出最长的正负交替的子序列(这里是通过删除某些数而得到的子序列),输出它们的最大和。
解析:找每一段连续正或负的最大值,累加即可。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<map> #include<set> using namespace std; typedef long long ll; const int maxn=2e5+10; const ll inf=0x3f3f3f3f3f; ll a[maxn]; int main() { int t; cin>>t; while(t--) { int n; cin>>n; ll maxx=0; ll sum=0; for(int i=0;i<n;i++) { cin>>a[i]; if(a[i]>0) { maxx=max(maxx,a[i]); } else { sum+=maxx; maxx=0; } } ll maxx2=-inf; for(int i=0;i<n;i++) { if(a[i]<0) { maxx2=max(maxx2,a[i]); } else { if(maxx2!=-inf) { sum+=maxx2; } maxx2=-inf; } } if(a[n-1]>0) //少加的情况。 sum+=maxx; else sum+=maxx2; cout<<sum<<endl; } return 0; }

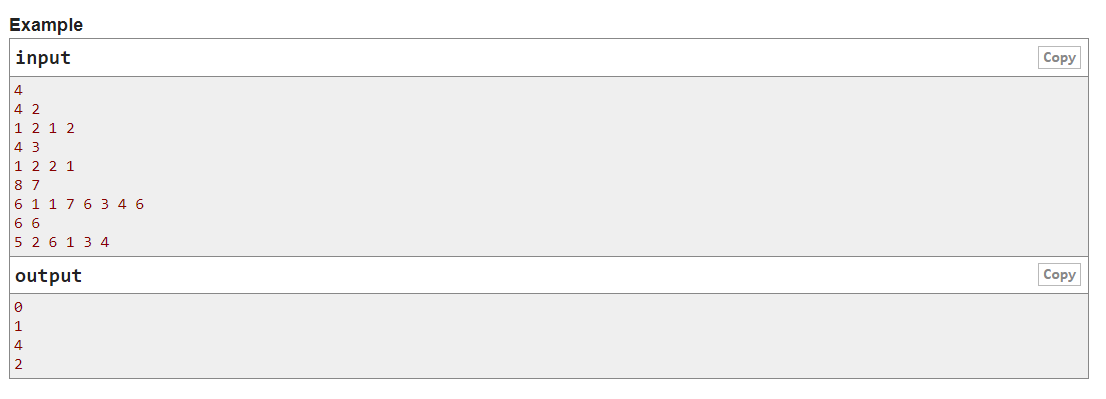
题意:给出偶数n个大小在[1,k]之间的数,操作是把任意一个数变成[1,k]之间的任意值。要达到每个ai+an-i+1都为定值x,求最少操作数。
解析:我刚开始想的是,记录x出现的最大次数maxx,输出n-maxx,调了半天。原来我忽略了,ai和an-i+1,并不是随便改一个值就能使和达到[2,k]的任意值的。所以去分析每个x所对应的修改次数,下面开始讨论:
sum=a[i]+a[n-i+1],maxx=max(a[i],a[n-i+1]),minn=min(a[i],a[n-i+1])
1.如果x范围位于[2,minn],就算把maxx改成1,它们的和也是大于这个范围的,所以需要改动两次。
2.如果x范围位于[minn+1,maxx+k],关于这个区间我解释一下:minn+1是把maxx变成1所得的和,maxx+k是把minn变成k所得的和,这是只改一个数所对应的和的范围。
3.除了上面两种,就剩下[maxx+k+1,2*k]了。它和第一种一样,就算把minn变成k,它们的和也是小于这个范围的,所以要修改两个值。
以上就需要差分数组维护了,关于差分数组,我有一篇博客可以参考:https://www.cnblogs.com/liyexin/p/11014218.html。对[L,R]每个数+1,就需要差分数组d[L]++,d[R+1]--。
较为啰嗦的更新代码:
for(int i=1;i<=n/2;i++) { ll sum=a[i]+a[n-i+1]; ll minn=min(a[i],a[n-i+1]); ll maxx=max(a[i],a[n-i+1]); d[2]+=2; d[minn+1]-=2; d[minn+1]++; d[maxx+k+1]--; d[maxx+k+1]+=2; d[2*k+1]-=2; d[sum]--; d[sum+1]++; //本来和就等于sum,所以不需要更新,需要--。 }
完整代码:
#include<iostream> #include<cstdio> #include<cstring> #include<iostream> #include<map> #include<queue> typedef long long ll; using namespace std; const int maxn=2e5+10; ll a[maxn],d[2*maxn]; //差分数组开两倍 int main() { int t; scanf("%d",&t); while(t--) { int n , k; scanf("%d%d",&n,&k); memset(d,0,sizeof(d)); for(int i=1;i<=n;i++) scanf("%lld",&a[i]); for(int i=1;i<=n/2;i++) { ll sum=a[i]+a[n-i+1]; ll minn=min(a[i],a[n-i+1]); ll maxx=max(a[i],a[n-i+1]); d[2]+=2; d[minn+1]-=2; d[minn+1]++; d[maxx+k+1]--; d[maxx+k+1]+=2; d[2*k+1]-=2; d[sum]--; d[sum+1]++; } ll minn=d[2]; for(int i=3;i<=2*k;i++) //x范围就是[2,2*k]看看哪一个x所需要的更新次数最少? { d[i]+=d[i-1]; minn=min(d[i],minn); } cout<<minn<<endl; } }


