Codeforces Round #630 (Div. 2) C. K-Complete Word(字符串)

地址：http://codeforces.com/contest/1332/problem/C

 

 

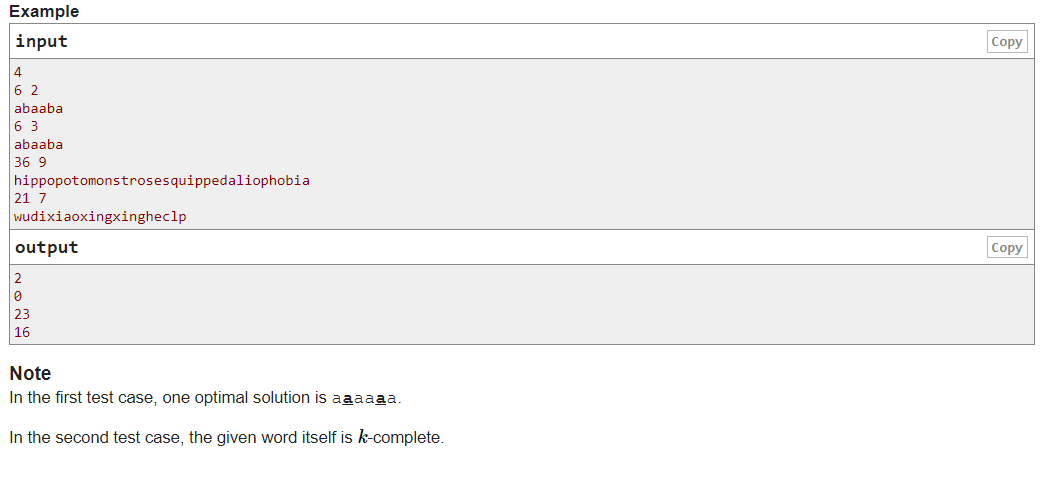
 　　　　题意：给出长度为n的字符串，将它分成长度为k的若干个循环节，要求这些循环节为回文。操作是对单个字符进行更换，问最少需要操作多少次。

　　　  解析：每个i，下个循环节就有对应的si==si+k。所以这些循环节是要完全相同的，且全为回文，也就能保证s为回文了。对这些单个循环节进行分析，每个i，对应等于k-i+1的位置。所以要统计单个循环节两边的对应位置的字母出现次数，找出出现次数最多的，把出现次数最小的变成它，每次的操作数是：sum=sum+n/k*2-maxx。统计时有个很好的代码：

for(int i=1;i<=k/2;i++)
        {
            int a[27]={0};
            for(int j=1;j<=n;j+=k)
            {
                a[s[i+j-1]-'a']++;
                a[s[j+k-i]-'a']++;
            }
}

　　　　每次i可以把所有循环节同一对称位置统计一遍，非常的方便。对于k为奇数的情况，会少统计中间，所以末尾再统计一次，sum=sum+n/k-maxx。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<set>
#include<map>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=2e5+10;
char s[maxn];
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n,k;
        scanf("%d%d",&n,&k);
        scanf("%s",s+1);
        int sum=0;
        for(int i=1;i<=k/2;i++)
        {
            int a[27]={0};
            for(int j=1;j<=n;j+=k)
            {
                a[s[i+j-1]-'a']++;
                a[s[j+k-i]-'a']++;
            }
            int maxx=-1;
            for(int j=0;j<27;j++)
            {
                if(maxx<a[j])
                    maxx=a[j];
            }
            sum+=n/k*2-maxx;
        }
        if(k%2!=0)
        {
            int i=k/2+1;
            int a[27]={0};
            for(int j=1;j<=n;j+=k)
            {
                a[s[i+j-1]-'a']++;

            }
            int maxx=-1;
            for(int j=0;j<27;j++)
            {
                if(maxx<a[j])
                    maxx=a[j];
            }
            sum+=n/k-maxx;
        }
        cout<<sum<<endl;
    }
}