三分算法

　　　　二分算法适用于单调函数。对于凸性或凹形函数，可以采用三分的做法。很简单，跟二分类似，只是这里需要两个mid。

 

 

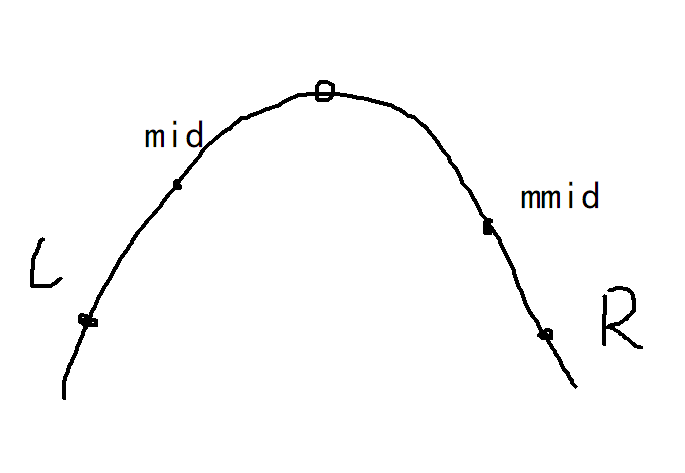
　　　　已知左右端点L,R,求峰值。第一个mid=(L+R)/2，第二个mmid=(R+mid)/2。判定方法和二分一致，思想就是无限逼近。对于凹形和凸性函数，写法不一样。下面给出模板。

　　　　凸性：

void tu()
{
    int l=1,r=n;
    while(l<r)
    {
        int mid=(l+r)/2;
        int mmid=(mid+r)/2;
        if(fc(mid)>fc(mmid))
        {
            r=mmid;
        }
        else
            l=mid;
    }
    for(int i=l;i<=r;i++)
        ans=max(ans,fc(i));
}

　　　　凹形：

void tu()
{
    int l=1,r=n;
    while(l<r)
    {
        int mid=(l+r)/2;
        int mmid=(mid+r)/2;
        if(fc(mid)>fc(mmid))
        {
            l=mid;
        }
        else
            r=mmid;
    }
    for(int i=l;i<=r;i++)
        ans=max(ans,fc(i));
}

　　　　对于while的终止条件，视具体情况而定。

　　　 HDU2899：http://acm.hdu.edu.cn/showproblem.php?pid=2899

 

 

 　　　 求函数最小值。

#include<iostream>
#include<vector>
#include<set>
#include<cmath>
using namespace std;    
#define eps 1e-9
double y;
double ac(double x)
{
    double ans;
    ans=6*x*x*x*x*x*x*x+8*x*x*x*x*x*x+7*x*x*x+5*x*x-y*x;
    return ans;
}
int main()
{
    int t;
    double mid,mmid;
    double r,l,ans1,ans2;
    cin>>t;
    while(t--)
    {
        cin>>y;
        r=100.0,l=0.0;
        while(r-l>=eps)
        {
            mid=(l+r)/2;
            mmid=(mid+r)/2;
            ans1=ac(mid);
            ans2=ac(mmid);
            if(ans1<ans2)
            {
                r=mmid;
            }
            else
                l=mid;
        }
        printf("%.4lf\n",ans1<ans2?ans1:ans2);
    }
}