Codeforces Round #621 (Div. 1 + Div. 2)

在csdn那里看到好多人用截图的方式，我也试试~

A:

 

 

 

 

 

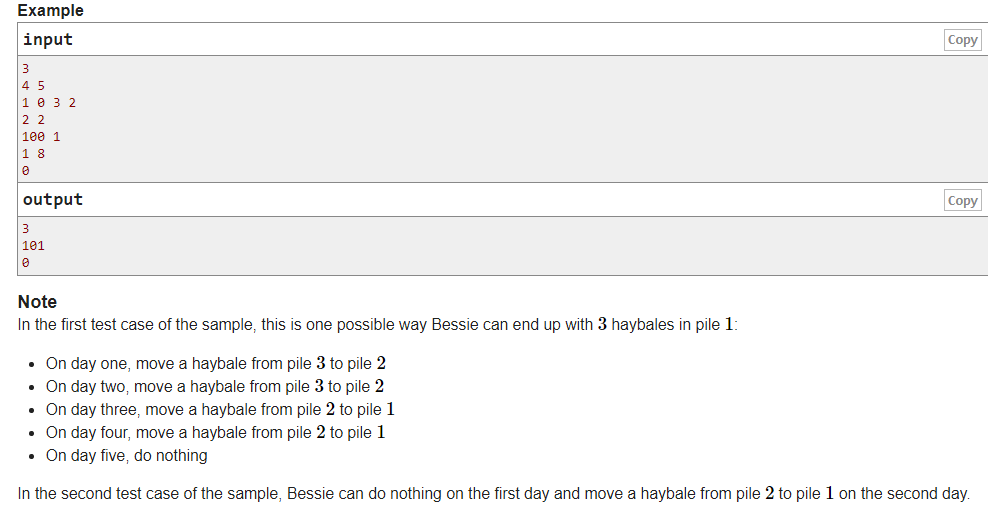 　　　　题意：把第一堆以外的其他堆往第一堆运，规定天数以内第一堆最多是多少

 

 

　　　　解析：简单模拟即可

#include<iostream>
#include<cstdio>
#include<stack>
#include<cstring>
#include<string>
using namespace std;
const int maxn=1e2+10;
int a[maxn];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n,d;
        cin>>n>>d;
        for(int i=1;i<=n;i++)
            cin>>a[i];
        for(int i=2;i<=n;i++)
        {
            int mid=0;
            while(a[i]>0&&d>0)
            {
                //cout<<d<<endl;
                mid++;
                d--;
                if(mid==i-1)
                {
                    a[i]--;
                    a[1]++;
                    mid=0;
                }
            }
        }
        cout<<a[1]<<endl;
    }
}

 

 

 

 

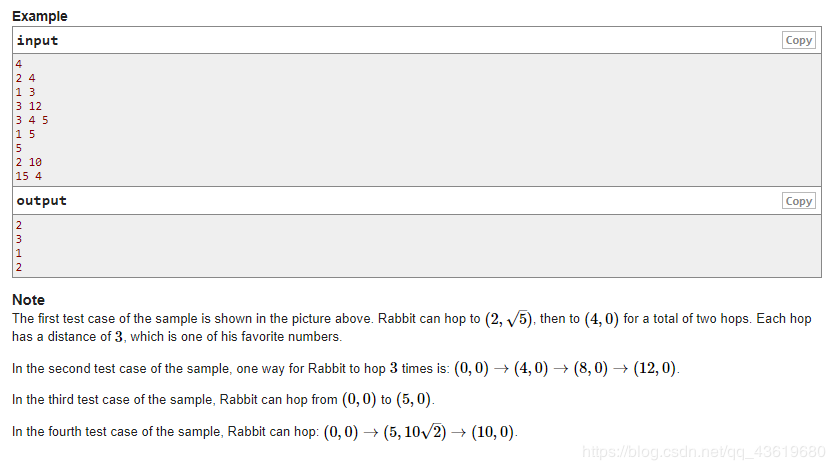
 　　　　题意：n,x，从(0,0)到达(x,0)，n种跳法，问最少需要跳几次到达x点。

　　　　 解析：这个题我要重点说一下了，实在是弄得我够呛，花了两个小时来找题解，分析，自己实在是笨的要死。

　　　　　　　 给定的n种跳法，我们只需要最大的即可。根据三角形，跳a，如果以此作为三角形，需要a+a>x，两边之和大于第三边，即:2*a>x，这个时候一上一下，只需要两步即可。对于不满足前这一条件的a，我们把它平铺就可以了，如果x%a==0，直接输出x/a，如果x%a!=0，那么就是x/a+1。为什么+1呢？比如样例x=12,   3,4,5。12%5==2，这个2怎么处理呢，我们只需要3个2就可以了，5，5，5, 把第2个5往上抬，和第三个5组成三角形即可到达x。因为12%5一定是小于5的，那么x%a+a一定是<2*a的，即一定可以构成一个三角形！+1即可。

　　　　　　　有个特判，如果n个跳法中出现了a==x，直接输出1即可。

　　　　　　　

#include<iostream>
#include<cstdio>
#include<stack>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
ll a[maxn];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        ll n,x;
        cin>>n>>x;
        int ok=0;
        for(int i=0;i<n;i++)
        {
            cin>>a[i];
            if(a[i]==x)
            {
                ok=1;
            }
        }
        if(ok)
        {
            cout<<'1'<<endl;continue;
        }
        sort(a,a+n);
        if(2*a[n-1]>=x)
        {
            cout<<"2"<<endl;continue;
        }
        int yu=x%a[n-1];
        if(yu==0)
        {
            cout<<x/a[n-1]<<endl;
        }
        else
        {
            cout<<x/a[n-1]+1<<endl;
        }
    }
}

 

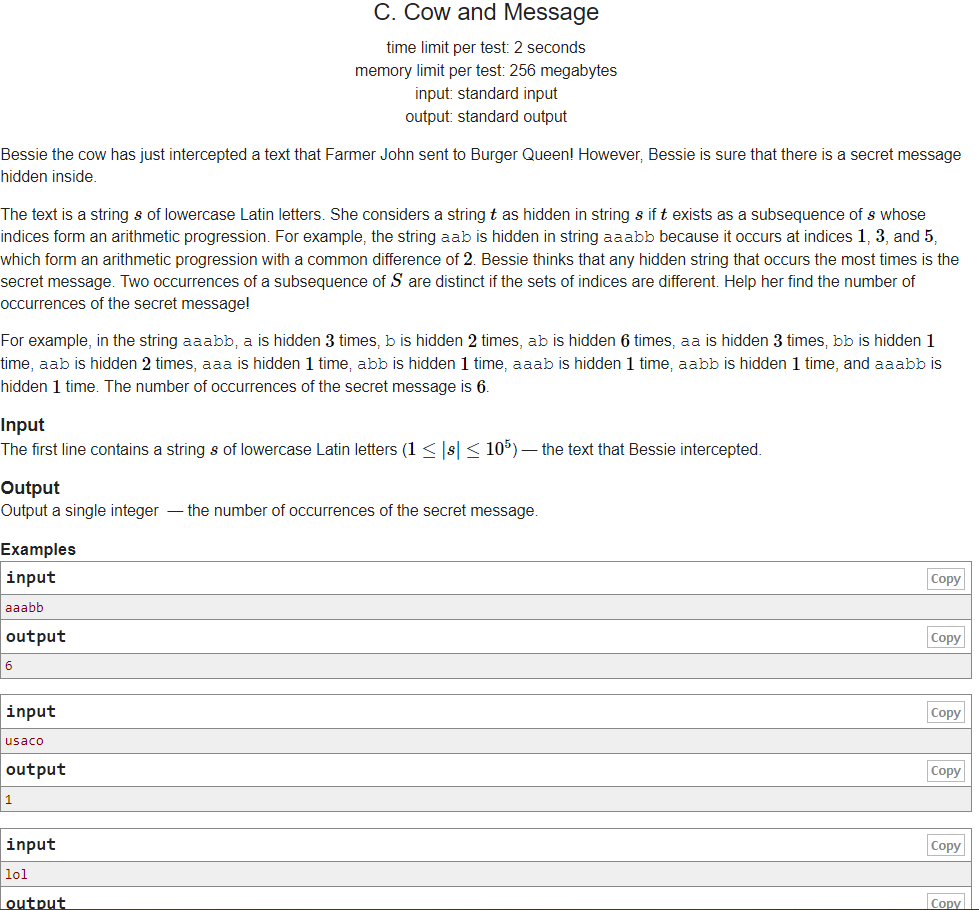
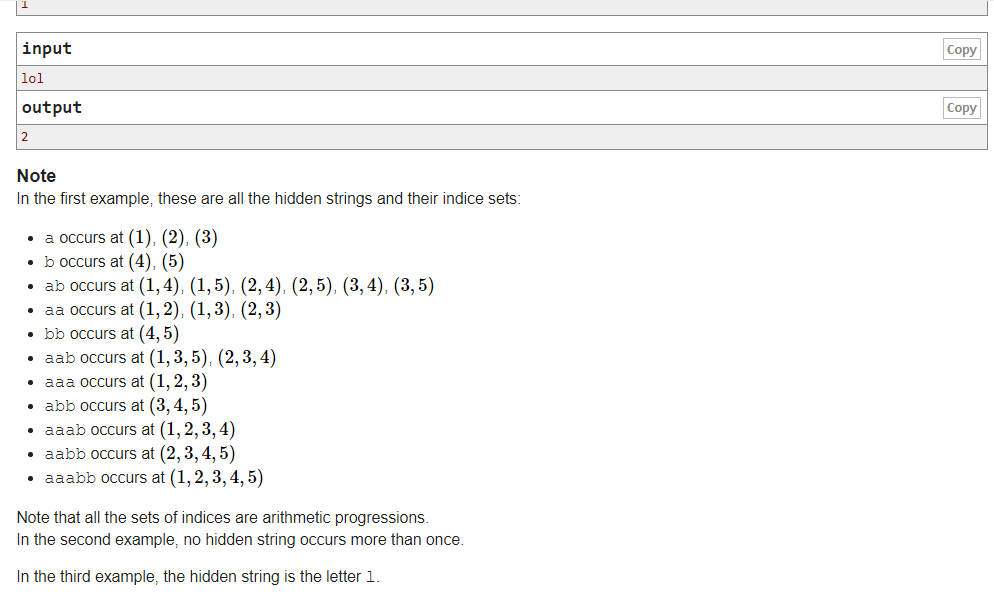
　　　　题意：给出一个字符串，找出出现最多的子串（出现的坐标点要呈等差数列，但是对于长度为1和2的没有影响）；如样例解释所示。

　　　 解析：观察一下，其实对于这个字符串，只有长度为1的和长度为2的值得考虑。因为如果对于一个长度为3的字符串，出现两次，那么其中的长度为2的字串出现次数一定是>=2的，也就是说长度为2的一定是比它们多的，更何况len>2时还有下标点呈等差的条件限制。统计单个的很简单，而对于长度为2的，需要一个m[26][26]，把每个单个的字符当作len=2的第2个字符，那么需要两个for更新每个以它为尾的字符串。出现次数：m[j][c]+=m[j]，这里有一个顺序问题，即：

    for(int i=0;i<len;i++)
    {
        int mid=s[i]-'a';    
        for(int j=0;j<26;j++)
            m[j][mid]+=num[j];    
        num[mid]++;　　//它放for(j)前面还是后面的问题
    }

　　　　　　为什么要放后面呢？因为放前面的话，那么就会出现多加的现象，比如输入aa，aa的出现次数变成了3，这很明显不对。我们只是让当前的字符为第二个而已，先加的话它是没有第一个字符的基础的，和谈第二个？输入a，m[a][a]=0，而不是=1。

#include<iostream>
#include<map>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
ll num[26],m[26][26];
int main()
{
    string s;
    cin>>s;
    ll len=s.length();
    for(int i=0;i<len;i++)
    {
        int mid=s[i]-'a';    
        for(int j=0;j<26;j++)
            m[j][mid]+=num[j];    
        num[mid]++;
    }
    ll max1=-1,max2=-1;
    for(int i=0;i<26;i++)
        max1=max(max1,num[i]);
    for(int i=0;i<26;i++)
        for(int j=0;j<26;j++)
            max2=max(max2,m[i][j]);
    cout<<max(max1,max2)<<endl;
}