D. On Sum of Fractions
Let's assume that
- v(n) is the largest prime number, that does not exceed n;
- u(n) is the smallest prime number strictly greater than n.
Find 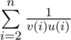 .
.
Input
The first line contains integer t (1 ≤ t ≤ 500) — the number of testscases.
Each of the following t lines of the input contains integer n (2 ≤ n ≤ 109).
Output
Print t lines: the i-th of them must contain the answer to the i-th test as an irreducible fraction "p/q", where p, q are integers, q > 0.
Sample test(s)
input
2
2
3
output
1/6
7/30
typedef long long LL ;
bool is_prime(LL x){
for(LL i = 2 ; i * i <= x ; i++)
if(x % i == 0)
return 0 ;
return 1 ;
}
LL V(LL x){
while(! is_prime(x))
x-- ;
return x ;
}
LL U(LL x){
x++ ;
while(! is_prime(x))
x++ ;
return x ;
}
LL gcd(LL x , LL y){
return y == 0 ? x : gcd(y , x % y) ;
}
class Node{
public :
LL zi ;
LL mu ;
public :
Node(){} ;
Node(LL z , LL m){
LL g = gcd(z , m) ;
zi = z/g ;
mu = m/g ;
} ;
Node operator + (const Node &other){
LL m , z , g ;
g = gcd(mu , other.mu) ;
m = mu / g * other.mu ;
z = other.mu / g * zi + mu /g * other.zi ;
g = gcd(z, m) ;
return Node(z/g , m/g) ;
}
Node operator - (const Node &other){
LL m , z , g ;
g = gcd(mu , other.mu) ;
m = mu / g * other.mu ;
z = other.mu /g * zi - mu / g * other.zi ;
g = gcd(z, m) ;
return Node(z/g , m/g) ;
}
Node & operator = (const Node &now){
this->mu = now.mu ;
this->zi = now.zi ;
return *this ;
}
friend ostream & operator << (ostream &out , const Node &A){
out<<A.zi<<"/"<<A.mu ;
return out ;
}
};
int main(){
int t ;
LL x ;
cin>>t ;
while(t--){
cin>>x ;
LL v = V(x) ;
LL u = U(x) ;
Node ans = Node(1 , 2) - Node(1 , v) ;
Node sum = Node(x-v+1, u*v) + ans ;
cout<<sum<<endl ;
}
return 0;
}




