卡特兰数:(是一个在计数问题中出现的数列)
一般项公式:
1.  或 2.
或 2. 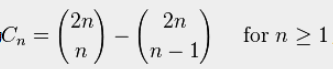
递归公式:
1.  或
或
2. 
注:全部可推导。
(性质:Cn为奇数时,必然出现在奇数项 2k-1。 (除去第 0 项))
应用举例:
1. 连乘的 n 个数加括号。 答案: Cn-1
2. 一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列? 答案:Cn
引申1:入栈看作 1 操作, 出栈看作 0 操作,则整个序列入栈出栈后从左到右遍历 1 和 0 组成的序列,1 的个数总是不小于 0 的个数,且 1 和 0 各 n(入栈 n 次,出栈 n 次) 个。因此, n 个 1 和 n 个 0 组成的全部满足条件 1 出现次数不少于 0 的序列数为: Cn
引申2: 将 1 看成 '(', 0 看成 ')', 则由 n 对 "()" 组成的有效序列 ['(' 在 ')' 之前] 个数为: Cn
3. n 个结点的二叉树个数: Cn
4. n+2边的凸多边形分三角形方法的个数: Cn
5. 平面上连接可以形成凸包的2n个点分成2个一组连成n条线段,两两线段之间不相交的情况总数是:Cn





