小算法笔记

素数： 除 1 外只能被 1 和自身整除的数。

方法一：

#include <stdio.h>
#define N 1000000
int num = 0;
int prime(int n)
{
	int i;
	if(n % 2 == 0)
		return (n == 2);//remove 1/2*n
	if(n % 3 == 0)
		return (n == 3);//remove 1/3*n
	if(n % 5 == 0)
		return (n == 5);//remove 1/5*n
	for(i = 7; i*i <= n; i += 2) //optimal for i < n^1/2
		if(n % i == 0)
			return 0;
	return 1;
}

void main()
{
	int i;
	for(i = 2; i < N; ++i)
		if(prime(i))
			printf("%-4d %d\n", ++num, i);
}

 

方法二（筛选法）：

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <time.h>
const int n = 10000000;
bool is_prime[n];

int main()
{
	int i, j, cnt = 0;
	clock_t time = clock();
	memset(is_prime, 0xff, sizeof(is_prime));
	//is_prime[0] = is_prime[1] = 0;
	int bound = (int)sqrt((float(n)));
	for(i = 2; i <= bound; ++i)
	{
		if(is_prime[i])
		{
			for(j = 2*i; j < n; j += i) 
				is_prime[j] = 0;
		}
	}
	for(i = 2; i < n; ++i) 
		if(is_prime[i]) 
			++cnt;
	printf("%dms, %d个素数\n", clock() - time, cnt);
	return 0;
}

 

set n = 1 000 000

 

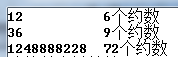
应用：求约数的个数：

#include <stdio.h>
int prime(int n)
{
	int i;
	if(n % 2 == 0)
		return (n == 2);//remove 1/2*n
	if(n % 3 == 0)
		return (n == 3);//remove 1/3*n
	if(n % 5 == 0)
		return (n == 5);//remove 1/5*n
	for(i = 7; i*i <= n; i += 2) //optimal for i < n^1/2
		if(n % i == 0)
			return 0;
	return 1;
}

void main()
{
	int k, i, tmp, cnt, ans;
	int D[] = {12, 36, 1248888228};
	for (k = 0; k < sizeof(D)/4; ++k) { // D[k]
		tmp = D[k], ans = 1;
		for (i = 2; i <= tmp; ++i) {
			cnt = 1;
			while (tmp % i == 0) { 
				tmp /= i;
				cnt++;
			}
			ans *= cnt;
		}
		printf("%-12d%d个约数\n", D[k], ans);
	}
}