判断链表是否有环，如果有，找到环的入口位置

Linked List Cycle

原题链接:Linked List Cycle

判断一个链表是否有环，空间复杂度是O(1)

如果不考虑空间复杂度，可以使用一个map记录走过的节点，当遇到第一个在map中存在的节点时，就说明回到了出发点，即链表有环，同时也找到了环的入口。

不适用额外内存空间的技巧是使用快慢指针，即采用两个指针walker和runner，walker每次移动一步而runner每次移动两步。当walker和runner第一次相遇时，证明链表有环

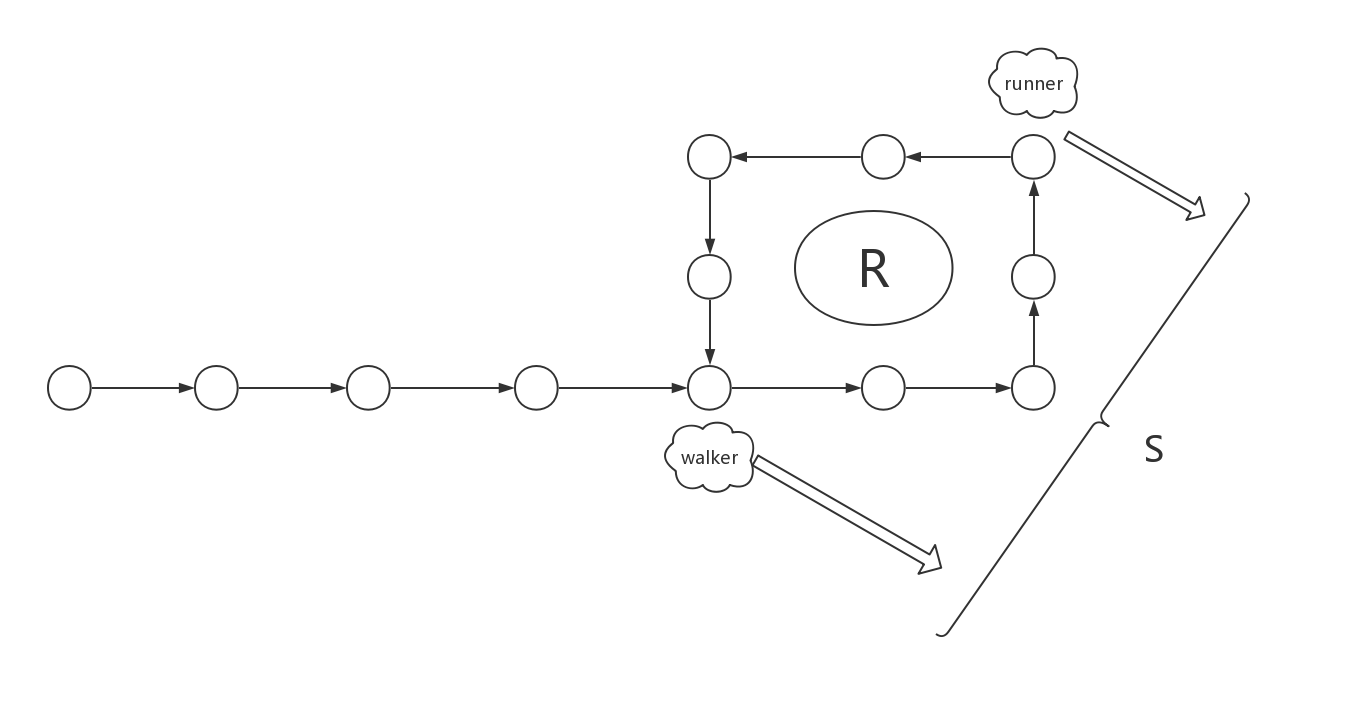
以图片为例，假设环的长度为R，当慢指针walker走到环入口时快指针runner的位置如图，且二者之间的距离为S。在慢指针进入环后的t时间内，快指针从距离环入口S处走了2t个节点，相当于从环入口走了S+2t个节点。而此时慢指针从环入口走了t个节点。

假设快慢指针一定可以相遇，那么有S+2t−t=nR，即S+t=nR，如果对于任意的S，R，n，总可以找到一个t满足上式，那么就可以说明快慢指针一定可以相遇，满足假设(显然可以找到)

而实际上，由于S<R，所以在慢指针走过一圈之前就可以相遇

所以如果链表中有环，那么当慢指针进入到环时，在未来的某一时刻，快慢指针一定可以相遇，通过这个也就可以判断链表是否有环

代码如下

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        auto walker = head;
        auto runner = head;
        while(runner && runner->next)
        {
            walker = walker->next;
            runner = runner->next->next;
            if(walker == runner)
                return true;
        }
        return false;
    }
};

Linked List Cycle II

原题链接:Linked List Cycle II

如果链表有环，寻找环入口位置

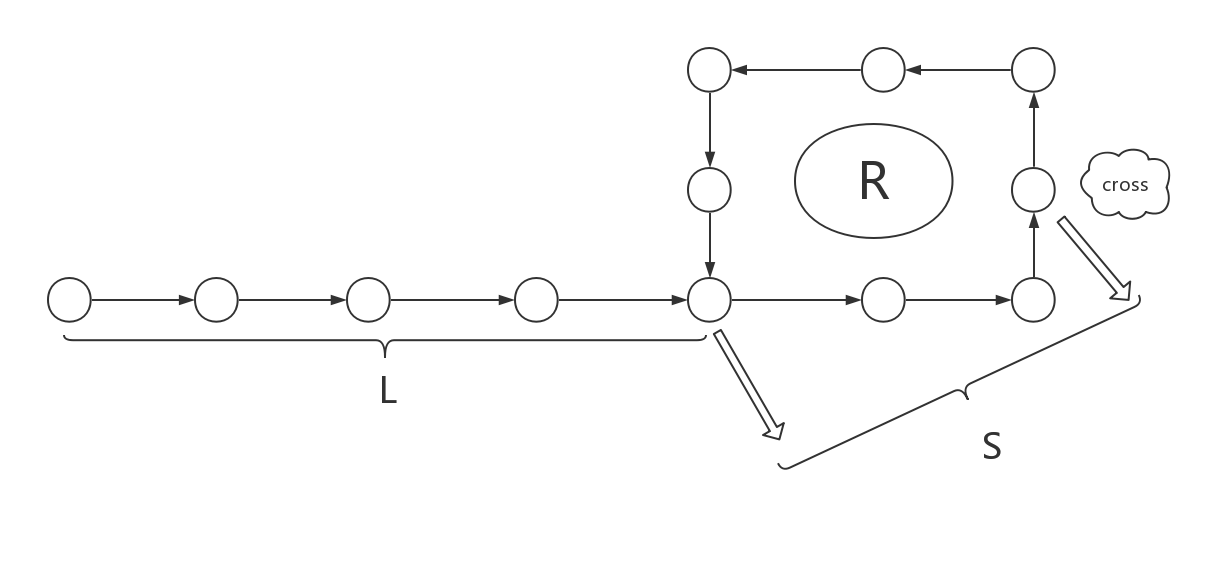
以图片为例，假设环入口距离链表头的长度为L，快慢指针相遇的位置为cross，且该位置距离环入口的长度为S。考虑快慢指针移动的距离，慢指针走了L+S，快指针走了L+S+nR(这是假设相遇之前快指针已经绕环n圈)。由于快指针的速度是慢指针的两倍，相同时间下快指针走过的路程就是慢指针的两倍，所以有2(L+S)=L+S+nR，化简得L+S=nR

当n=1时，即快指针在相遇之前多走了一圈，即L+S=R，也就是L=R−S，观察图片，L表示从链表头到环入口的距离，而R−S表示从cross继续移动到环入口的距离，既然二者是相等的，那么如果采用两个指针，一个从表头出发，一个从cross出发，那么它们将同时到达环入口。即二者相等时便是环入口节点

当n>1时，上式为L=nR−S，LL仍然表示从链表头到达环入口的距离，而nR−S可以看成从cross出发移动nR步后再倒退SS步，从cross移动nRnR步后回到cross位置，倒退S步后是环入口，所以也是同时到达环入口。即二者相等时便是环入口节点

所以寻找环入口的方法就是采用两个指针，一个从表头出发，一个从相遇点出发，一次都只移动一步，当二者相等时便是环入口的位置

代码如下

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        auto walker = head;
        auto runner = head;
        while(runner && runner->next)
        {
            walker = walker->next;
            runner = runner->next->next;
            if(walker == runner)
                break;
        }
        if(!runner || !runner->next)
            return nullptr;
        auto headWalker = head;
        auto crossWalker = walker;
        while(headWalker != crossWalker)
        {
            headWalker = headWalker->next;
            crossWalker = crossWalker->next;
        }
        return headWalker;
    }
};

其它的和环有关的题目记得还有

求环的长度

第一种方法是利用上面求出的环入口，再走一圈就可以求出长度，代码如下

int cycleLen(ListNode* head)
{
    auto cycleIn = detectCycle(head);
    int len = 1;
    auto walker = cycleIn;
    while(walker->next != cycleIn)
    {
        ++len;
        walker = walker->next;
    }
    return len;
}

第二种方法是当快慢指针相遇时，继续移动直到第二次相遇，此时快指针移动的距离正好比慢指针多一圈，代码如下

int cycleLen(ListNode* head)
{
    auto walker = head;
    auto runner = head;
    while(runner && runner->next)
    {
        walker = walker->next;
        runner = runner->next;
        if(walker == runner)
            break;
    }
    int len = 0;
    while(runner && runner->next)
    {
        ++len;
        walker = walker->next;
        runner = runner->next;
        if(walker == runner)
            break;
    }
    return len;
}

from：https://blog.csdn.net/sinat_35261315/article/details/79205157