常用排序算法实现与效率比较

排序综述

　　所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。排序算法，就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视，尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。在各个领域中考虑到数据的各种限制和规范，要得到一个符合实际的优秀算法，得经过大量的推理和分析。

冒泡排序法

排序规则

冒泡排序算法的运作如下：（从后往前）
1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

稳定性:冒泡排序是一种稳定排序算法

算法实现

实现思路

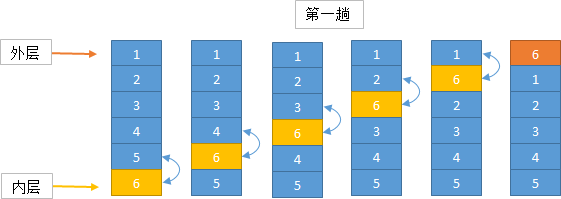
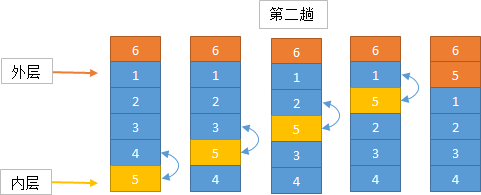
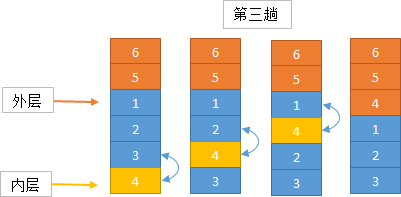
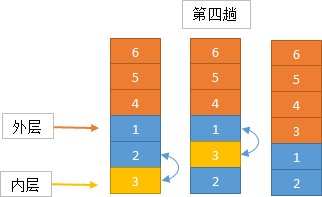
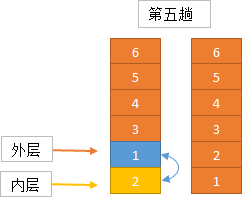
算法实现

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 //冒泡排序(升序)
 5 void bubbleSort(int *array, int len)    //O(n?)
 6 {
 7 #if 1
 8     // 外层
 9     for (int i = 0; i < len; ++i)
10     {
11         for (int j = 1; j < len - i; j++)
12         {
13             // 交换
14             if (array[j] < array[j - 1])
15             {
16                 int tmp = array[j];
17                 array[j] = array[j - 1];
18                 array[j - 1] = tmp;
19             }
20         }
21     }
22 #else  //冒泡排序改进版
23     // 0: 没有排好, 1: 已经排好
24     int flag = 0;
25     for (int i = len - 1; i > 0 && flag == 0; --i)
26     {
27         flag = 1;    // 默认已经排好
28         for (int j = 0; j < i; ++j)
29         {
30             if (array[j] > array[j + 1])
31             {
32                 int tmp = array[j];
33                 array[j] = array[j + 1];
34                 array[j + 1] = tmp;
35                 flag = 0;    // 没有排好
36             }
37         }
38     }
39 #endif
40 }

选择排序法

排序规则

　　它的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

稳定性:选择排序是不稳定的排序方法 如:[5,5,3]

 算法实现

实现思路

 

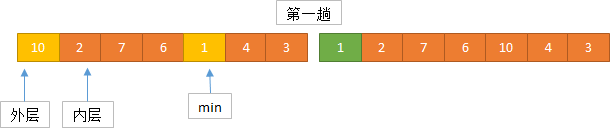
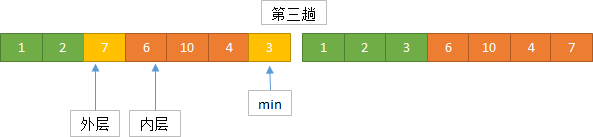
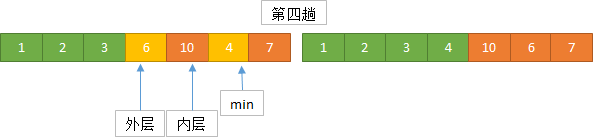
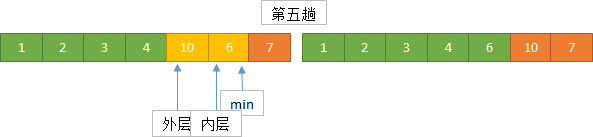
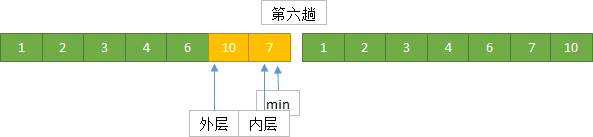
算法实现

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 //选择排序(升序排列)
 5 void selectionSort(int *array, int len)
 6 {
 7     int min = 0;    // 指向最小的元素的位置
 8                     // 外层循环
 9     for (int i = 0; i < len - 1; ++i)
10     {
11         min = i;
12         // 内存循环
13         for (int j = i + 1; j < len; ++j)
14         {
15             // 判断
16             if (array[min] > array[j])
17             {
18                 // 保存最小的元素的位置
19                 min = j;
20             }
21         }
22         // 判断是否需要交换
23         if (min != i)
24         {
25             // 找到了新的最小值
26             // 交换
27             int tmp = array[min];
28             array[min] = array[i];
29             array[i] = tmp;
30         }
31     }
32 }

 

插入排序法

排序思想

排序规则

　　每次处理就是将无序数列的第一个元素与有序数列的元素从后往前逐个进行比较，找出插入位置，将该元素插入到有序数列的合适位置中。

稳定性:插入排序是稳定的。

算法实现

实现思路

 

算法实现

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 //插入排序算法(升序排列)
 5 void insertionSort(int *array, int len)
 6 {
 7     int tmp = 0;    // 存储基准数
 8     int index = 0;    // 坑的位置
 9                     // 遍历无序序列
10     for (int i = 1; i < len; ++i)
11     {
12         index = i;
13         tmp = array[i];
14         // 遍历有序序列(从后往前)
15         for (int j = i - 1; j >= 0; --j)
16         {
17             // 基准数根有序序列中的元素比较
18             if (tmp < array[j])
19             {
20                 // 有序序列元素后移
21                 array[j + 1] = array[j];
22                 // 坑的位置
23                 index = j;
24             }  
25         }
26         // 填坑
27         array[index] = tmp;
28     }
29 }

希尔排序法

排序思想

　　希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

稳定性: 希尔排序是非稳定排序算法。

算法实现

实现思路

 

 

 

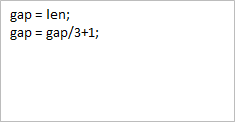
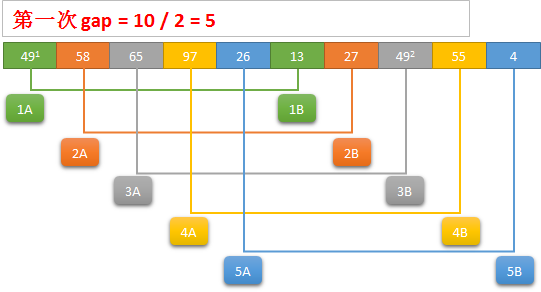
算法实现

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 //希尔排序
 5 void shellSort(int *array, int len)
 6 {
 7     // 步长
 8     int gap = len;
 9     while (gap > 1)
10     {
11         // 步长递减公式
12         gap = gap / 3 + 1;
13         // 分组, 对每一组, 进行插入排序
14         for (int i = 0; i < gap; ++i)
15         {
16             int tmp;    // 基准数
17             int index;    // 坑的位置
18                         // 插入排序
19                         // 无序序列
20             for (int j = i + gap; j < len; j += gap)
21             {
22                 tmp = array[j];
23                 index = j;
24                 // 有序序列(从后往前遍历)
25                 for (int k = j - gap; k >= 0; k -= gap)
26                 {
27                     if (tmp < array[k])
28                     {
29                         // 后移
30                         array[k + gap] = array[k];
31                         // 位置
32                         index = k;
33                     }
34                     else
35                     {
36                         break;
37                     }
38                 }
39                 // 填坑
40                 array[index] = tmp;
41             }
42         }
43     }
44 }

快速排序法

排序规则

快速排序：挖坑排序+分治法

分治法的基本思想是：

1．先从数列中取出一个数作为基准数。

2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。

3．再对左右区间重复第二步，直到各区间只有一个数。

算法实现

实现思路

 

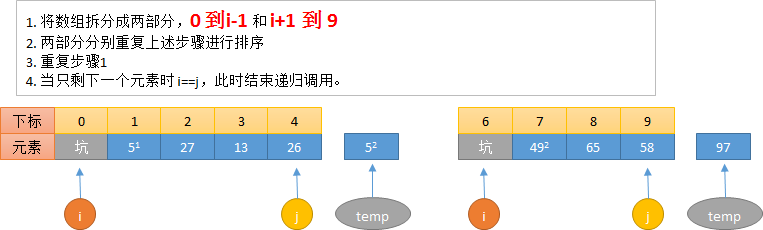
算法实现

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 //快速排序(从小到大)
 5 void quickSort(int s[], int l, int r)
 6 {
 7     if (l < r)
 8     {
 9         int i = l, j = r;
10         // 拿出第一个元素, 保存到x中,第一个位置成为一个坑
11         int x = s[l];
12         while (i < j)
13         {
14             // 从右向左找小于x的数
15             while (i < j && s[j] >= x)
16             {
17                 //左移, 直到遇到小于等于x的数
18                 j--;
19             }
20             if (i < j)
21             {
22                 //将右侧找到的小于x的元素放入左侧坑中, 右侧出现一个坑
23                 //左侧元素索引后移
24                 s[i++] = s[j];
25             }
26 
27             // 从左向右找大于等于x的数
28             while (i < j && s[i] < x)
29             {
30                 //右移, 直到遇到大于x的数
31                 i++;
32             }
33             if (i < j)
34             {
35                 //将左侧找到的元素放入右侧坑中, 左侧出现一个坑
36                 //右侧元素索引向前移动
37                 s[j--] = s[i];
38             }
39         }
40         //此时 i=j,将保存在x中的数填入坑中
41         s[i] = x;
42         quickSort(s, l, i - 1); // 递归调用 
43         quickSort(s, i + 1, r);
44     }
45 }

归并排序法

排序规则

归并排序: 空间换时间

算法实现

实现思路

 

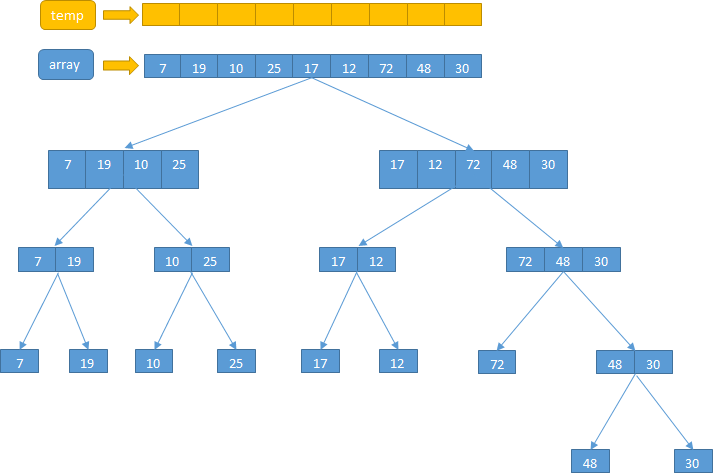
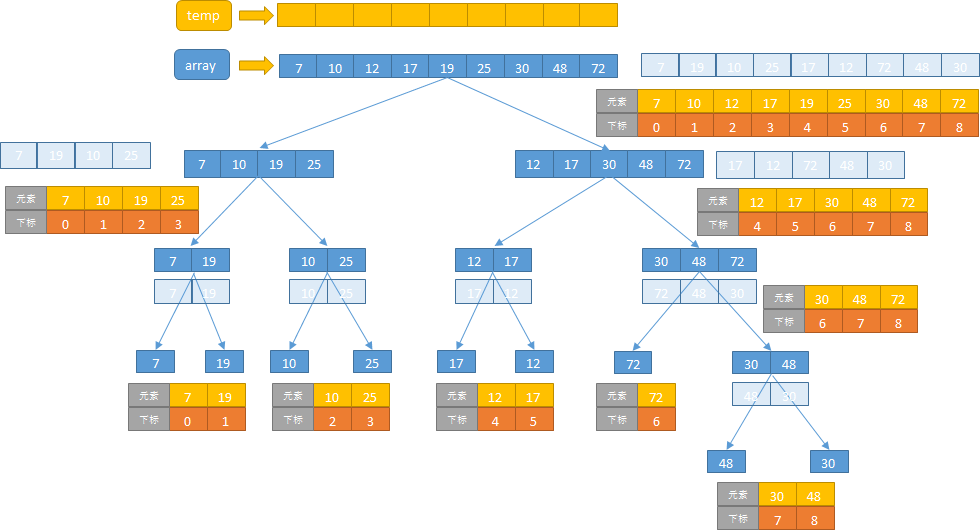
算法实现

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 //将两个有序数列a[first...mid]和a[mid+1...last]合并。
 5 void mergeArray(int a[], int first, int mid, int last, int temp[])
 6 {
 7     int leftStart = first;    //左有序序列起点
 8     int leftEnd = mid;    //左有序序列终点
 9     int rightStart = mid + 1;    //右有序序列起点
10     int rightEnd = last;    //右有序序列终点
11     int length = 0;    //两个有序序列合并之后的有序序列长度
12     int i = leftStart, j = rightStart;
13 
14     //将两个有序序列中的元素合并到第三个有序序列中(a的左半部分和右半部分合并到temp中)
15     while (i <= leftEnd && j <= rightEnd)
16     {
17         //按照从小到大的顺序放入到temp中
18         if (a[i] <= a[j])
19         {
20             temp[length++] = a[i++];
21         }
22         else
23         {
24             temp[length++] = a[j++];
25         }
26     }
27     //如果左半部分还有元素, 直接放到temp中
28     while (i <= leftEnd)
29     {
30         temp[length++] = a[i++];
31     }
32     //如果右半部分还有元素, 直接放到temp中
33     while (j <= rightEnd)
34     {
35         temp[length++] = a[j++];
36     }
37     //将temp中排好的序列拷贝到a数组中
38     for (i = 0; i < length; i++)
39     {
40         //只替换已排好序的那一部分
41         a[leftStart + i] = temp[i];
42     }
43 }
44 
45 //归并排序
46 void mergeSort(int a[], int first, int last, int temp[])
47 {
48     if (first < last)
49     {
50         //找到数组的中间位置
51         int mid = (first + last) / 2;
52         //左边有序
53         mergeSort(a, first, mid, temp);
54         //右边有序
55         mergeSort(a, mid + 1, last, temp);
56         //再将二个有序数列合并
57         mergeArray(a, first, mid, last, temp);
58     }
59 }

 

效率比较

测试代码

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 #include <time.h>    //利用时间生成种子
 4 #include <math.h>
 5 #include <sys/timeb.h>
 6 #include "sort.h"
 7 
 8 //效率测试
 9 #define NUMBER 30000
10 
11 //获取系统时间,精确到毫秒
12 long long getSystemTime()
13 {
14     struct timeb t;
15     ftime(&t);
16     return 1000 * t.time + t.millitm;
17 }
18 
19 //生成随机数
20 void randNumber(int* array, int len)
21 {
22     int i;
23     //生成种子
24     srand((unsigned)time(NULL));
25     for (i = 0; i < len; ++i)
26     {
27         //生成一个小于len的随机数
28         array[i] = rand() % len;
29     }
30 }
31 
32 int main()
33 {
34     int i, j;
35     int array[6][NUMBER];
36     long long t_start, t_end, t_used;
37 
38     //生成种子
39     srand((unsigned)time(NULL));
40     for (i = 0; i < NUMBER; ++i)
41     {
42         //生成一个小于len的随机数
43         int number = rand() % NUMBER;
44         for (j = 0; j < 6; ++j)
45         {
46             array[j][i] = number;
47         }
48     }
49 
50     //冒泡排序
51     t_start = getSystemTime();
52     bubbleSort(array[0], NUMBER);
53     t_end = getSystemTime();
54     t_used = t_end - t_start;
55     printf("冒泡排序对 %d 个数进行排序，耗时: %lld ms\n", NUMBER, t_used);
56 
57     //选择排序
58     t_start = getSystemTime();
59     selectionSort(array[1], NUMBER);
60     t_end = getSystemTime();
61     t_used = t_end - t_start;
62     printf("选择排序对 %d 个数进行排序，耗时: %lld ms\n", NUMBER, t_used);
63 
64     //插入排序
65     t_start = getSystemTime();
66     insertionSort(array[2], NUMBER);
67     t_end = getSystemTime();
68     t_used = t_end - t_start;
69     printf("插入排序对 %d 个数进行排序，耗时: %lld ms\n", NUMBER, t_used);
70 
71     //希尔排序
72     t_start = getSystemTime();
73     shellSort(array[3], NUMBER);
74     t_end = getSystemTime();
75     t_used = t_end - t_start;
76     printf("希尔排序对 %d 个数进行排序，耗时: %lld ms\n", NUMBER, t_used);
77 
78     //归并排序
79     int temp[NUMBER];
80     t_start = getSystemTime();
81     mergeSort(array[4], 0, NUMBER - 1, temp);
82     t_end = getSystemTime();
83     t_used = t_end - t_start;
84     printf("归并排序对 %d 个数进行排序，耗时: %lld ms\n", NUMBER, t_used);
85 
86     //快速排序
87     t_start = getSystemTime();
88     quickSort(array[5], 0, NUMBER - 1);
89     t_end = getSystemTime();
90     t_used = t_end - t_start;
91     printf("快速排序对 %d 个数进行排序，耗时: %lld ms\n", NUMBER, t_used);
92 
93     return 0;
94 }

 

运行结果

 

结论

　　根据效率测试代码运行结果，以上6种排序方式对于30000个数据的排序效率显而易见。

posted @ 2019-05-19 17:36  鲸小鱼-  阅读(734)  评论(0)  编辑  收藏  举报