小学生都能看懂的表达式计算（图解）

基础知识

会加减乘除（纳尼，这个还有不会的吗）

会双向链表和树（纳尼，还个还要会吗）

温故知新

表达式 2 + 3 - 4 + 5，人类计算的过程是这样的，如下图：

因为加减操作符优先级相同，所以从左到右依次运算。

可计算机不会这样啊，必须先转化为一棵树（AST，抽象语法树，这是编译原理中的概念）才行，如下图：

操作符上提变为根节点，左右操作数下降变为叶子节点，它们整体又成了一个操作数。依次对每个操作符使用这个规则，表达式即可变成一棵树。

再接再厉

表达式 2 + 3 × 4 - 5 ÷ 6，人类的计算过程是这样的，如下图：

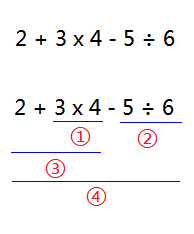
按照优先级从高到低，先乘除，再加减。

要想让计算机来算啊，还得先转换为一棵AST才行，如下图：

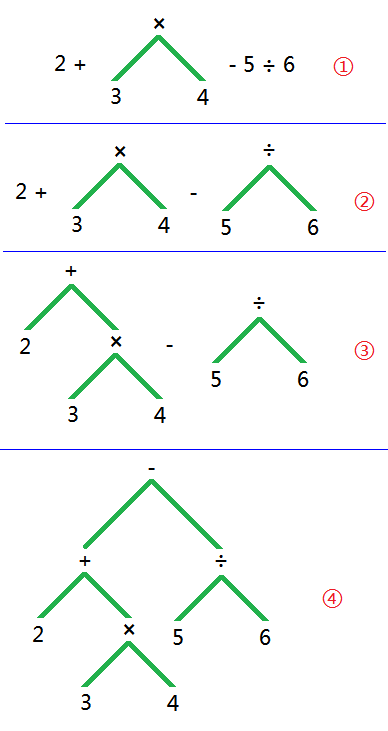
发现问题

综上，不难发现，先要把一个表达式转化为一棵AST。人类根据操作符的优先级很自然地把一个表达式转化为一棵树，但是计算机该怎么做呢？

模仿人类

人类的视线可以在表达式上随意扫描，对于不复杂的，一眼就发现优先级高的操作符，瞬间拿到它两边的操作数，就可以进行转化了。

计算机在方式上无法和人类相比，但是在结果上必须要相同，即也要找到优先级高的操作符，也要知道它两边的操作数，然后再进行转化。

回归程序

定义一下操作符的优先级，优先级的数值没有要求，如下图：

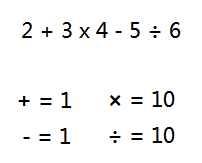
当我们拿到一个操作符时，也要能拿到它左右两边的操作数，因操作符和操作数是间隔互联的，实际它们就是一个双向链表。

因我们要找出优先级高的操作符，所以必须先找出所有的操作符，然后再判断优先级的高低。

把整个表达式里的操作数和操作符用双向链表串起来，并把所有的操作符放入一个列表里。如下图：

按优先级从高到低对操作符列表排序，优先级高的前移，优先级低的后移，优先级相同的相对位置不变。如下图：

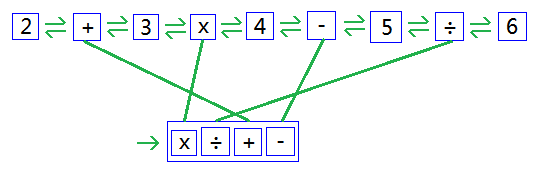
取出排在第一位的×，去双向链表里找出它的左右操作数3和4，把这三个节点转化为一棵树，再把该树作为操作数替换掉原来的三个节点，同时修复好与前面 + 号和后面 - 号的双向链接。如下图：

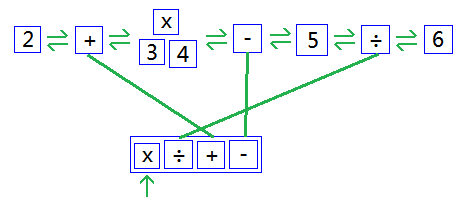
取出第二位的÷，采用和上面相同的方式进行转化。如下图：

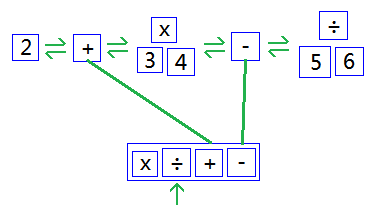
取出第三位的+，采用相同的方式转化。如下图：

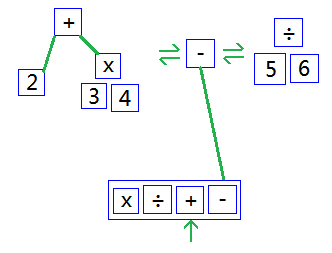
取出最后一位的-，采用相同的方式转化后，整个表达式转化完毕，变为一棵AST。如下图：

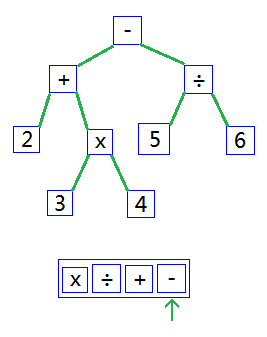
推而广之

操作符有了优先级之后，就限制了表达式的计算顺序，人们有时希望打破这种限制，就引入了更神奇的操作符，就是小括号啦（哈哈）。

表达式 ( 2 + 3 ) × ( ( 4 - 5 ) ÷ 6 )，如果还想采用上面的套路，那么核心问题就落到了操作符的优先级上了。即如何真实地反映每个操作符的优先级值。

此时我们意识到，操作符的优先级不再是固定的，而是会随着有没有括号以及括号的嵌套深度而变化。其实小括号本来就是改变了操作符的优先级嘛，我们人类明白这一点，关键也要让计算机明白。

既然括号是操作符，那也为它定义一个优先级值，这个值最好稍微大一些。如下图：

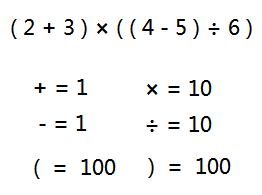
定义一个上下文的基础优先级值，默认当然是0了。

当遇到左括号时，基础优先级值加上括号优先级值，相当于基础优先级值得到了提升，这样括号里的操作符因为有基础优先级值的存在，所以自然抬高了自己的优先级值（相等于站到了巨人的肩膀上）。

当遇到右括号时，基础优先级值减去括号优先级值，相当于此时新的基础优先级值降到了进入括号前的水准。如下图：

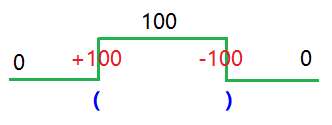
解析表达式，同时计算出每个操作符的优先级值（牢记，遇到一个左括号加100，遇到一个右括号减100）。如下图：

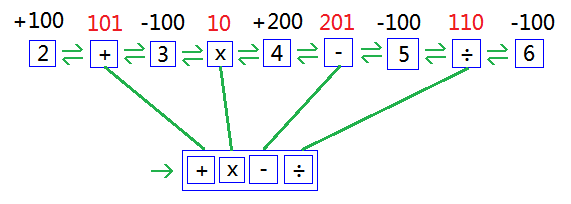
按照实际优先级值从高到低排序操作符列表。如下图：

最后按照相同的方式，转换为一棵AST。如下图：

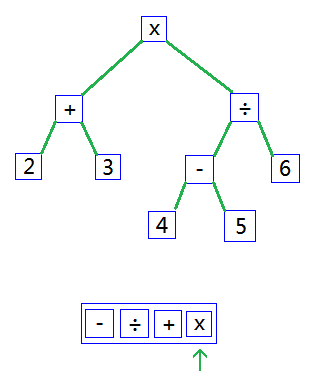
后记：人类社会存在的历史要比计算机的历史长的多，从人类社会寻找问题的解决思路有时也是一个不错的方向。甚至可以从大自然中寻找。

（完）

编程新说

---

用独特的视角说技术