Arch-乘法器实现及简单优化
乘法器实现概述
1. 如何实现乘法
本质上，我们是使用”列竖式“一般的方法，即通过移位和加法来实现乘法。步骤如下：
-
在每个周期判断乘数的最低位，如果为 1，那么加到 ans 中。此后将乘数右移一位，将被乘数左移一位，进入下一个周期。
-
重复 16 次。
同时，我们也需要考虑补码的一些性质。以 16 位乘 16 位为例，注意到：
\[y=-y_{15}\times2^{15} +\sum_{i=0}^{14}{y_i\times2^i}
\]
且 \([x+y]_c=[x]_c+[y]_c\), \([x <<i]_c=[x]_c<<i\) 。
于是有：
\[[xy]_c=[x]_c\cdot(-y_{15}\times2^{15} +\sum_{i=0}^{14}{y_i\times2^i})
\]
即只有最后一位需要进行减法，其余部分都是加法。
2. 一些乘法优化
2.1 Booth 一位乘算法
注意到如下式子：
\[\begin{aligned}
& y=-y_{15}\times2^{15} +\sum_{i=0}^{14}{y_i\times2^i}\\
& \ \ =-y_{15}\times2^{15}+y_{14}\times2^{15}-y_{14}\times2^{14}+\cdot\cdot\cdot+y_0\times2^1-y_0\times2^0\\
& \ \ =\sum_{i=0}^{15}{(y_{i-1}-y_i)\times2^i}
\end{aligned}
\]
其中 \(y_{-1}:=0\)。根据此公式，我们的式子变得更加规整，也不需要对最后一位特殊操作。同时，也可以优化掉部分情况（例如 \(y_i=1\) 且 \(y_{i-1}=1\)）。
2.2 Booth 两位乘算法
注意到如下式子：
\[\begin{aligned}
& y=-2\times y_{15}\times2^{14}+y_{14}\times2^{14}+(2^{14}-2\times2^{12})\times y_{13}+\cdot\cdot\cdot+y_{-1}\times2^0\\
&\ \ = \sum_{i=0}^{7}{2^{2i}}\times(y_{2i}+y_{2i-1}-2y_{2i+1})
\end{aligned}
\]
由此我们可以推导出 Booth 两位乘法的运算规则：
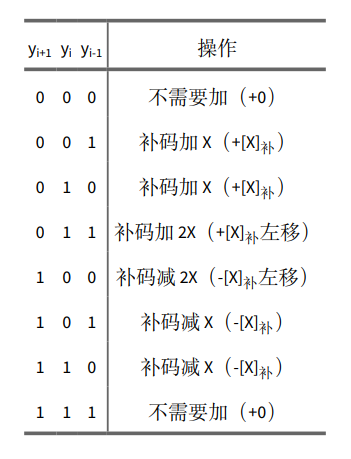
这样可以将运算时间减半。另外，也可以实现 3 位以上的 Booth 乘法，但这样的话处理会比较麻烦。
3. 代码实现
module multiplier (
input signed [15:0] A,
input signed [15:0] B,
output reg signed [31:0] mul
);
reg signed [31:0] ans;
reg signed [31:0] origin_a;
reg signed [31:0] minus_a;
reg signed [31:0] double_a;
reg signed [31:0] neg_double_a;
reg [15:-1] extend_b;
reg signed [4:0] i;
always @(A, B) begin
origin_a = {{16{A[15]}}, A[15:0]};
minus_a = ~origin_a + 1;
double_a = origin_a << 1;
neg_double_a = ~double_a + 1;
extend_b = {B[15:0], 1'b0};
ans = 0;
for (i = 14; i >= 0; i = i - 2) begin
if (extend_b[i + 1] == 1'b0 && extend_b[i] == 1'b0 && extend_b[i - 1] == 1'b0) begin
// do nothing
end
if (extend_b[i + 1] == 1'b0 && extend_b[i] == 1'b0 && extend_b[i - 1] == 1'b1) begin
ans = ans + A;
end
if (extend_b[i + 1] == 1'b0 && extend_b[i] == 1'b1 && extend_b[i - 1] == 1'b0) begin
ans = ans + A;
end
if (extend_b[i + 1] == 1'b0 && extend_b[i] == 1'b1 && extend_b[i - 1] == 1'b1) begin
ans = ans + double_a;
end
if (extend_b[i + 1] == 1'b1 && extend_b[i] == 1'b0 && extend_b[i - 1] == 1'b0) begin
ans = ans + neg_double_a;
end
if (extend_b[i + 1] == 1'b1 && extend_b[i] == 1'b0 && extend_b[i - 1] == 1'b1) begin
ans = ans + minus_a;
end
if (extend_b[i + 1] == 1'b1 && extend_b[i] == 1'b1 && extend_b[i - 1] == 1'b0) begin
ans = ans + minus_a;
end
if (extend_b[i + 1] == 1'b1 && extend_b[i] == 1'b1 && extend_b[i - 1] == 1'b1) begin
// do nothing
end
if (i != 0) ans = ans << 2;
end
end
always @(A, B) begin
# 20;
mul = ans;
end
endmodule
