动态规划 ------背包问题
课件的内容来自于视频: https://www.youtube.com/watch?v=FDzOqoyQ-jM
背包问题的描述:
背包的重量限定为 b ,每个物品可以放 >=1个,为了获得最大的价值!

把这个实际问题抽象成数学问题,建立模型
Xi表示 装入背包的第 i 种物品的个数。 可以是 1 , 2, 3 。。。。[ b/w] ,这里表示取整数。

动态规划问题的关键步骤,怎么进行子问题的界定
总共有 n 种物品, 背包的限定重量为 b ,那么,子问题是 : 总共可以供选择的 商品 为0, 1,2 ,3 ,。。。 .k (这里的k小于等于n)
背包的限重的取值是 0,1,2,3,。。。。。y (这里的y小于等于 b)
当 k的取值是 n, y 的取值是 b, 就是这个大问题啦

递推方程的表达式:
这个递推式的理解,考虑第 k 个商品放不放入背包。F(k-1) 的意思就是说,我们不放入 第 k个商品,此时的最大价值
F(k) 表示的是放入第 k 个商品,那么,背包剩下能够承受的重量就是 y-wk , wk表示的是 第k个商品的重量
我们要得到的就是 这两种情况的最大值,所以,要max。
装第 0 种商品,当然,我们的价值为0.
装第 1 种商品,那么,最多可以装 [ y/wb] ,这里是取整数, 如果 某个商品的重量大于背包所承受的重量,,也就是说, 在 Fk(y-Wk)这项里, y-Wk的 的值可能小于0,那么,我们令Fk(y)为负无穷,这样,我们就保证了在Max的时候,不考虑这个最小值,而是取另外一项作为结果。

下面讨论 标记函数。为找到最后的解

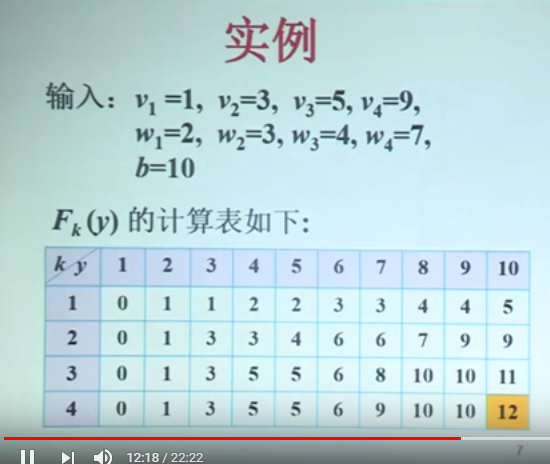
具体的例子: 这里的物品可以放多个。
追踪解:
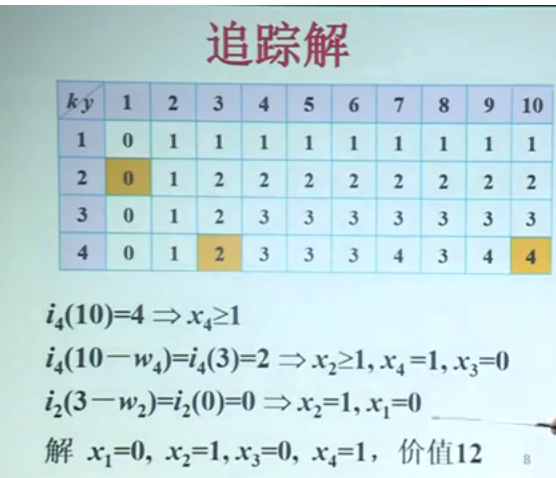
追踪算法

时间复杂度:

推广:


posted on 2017-09-29 21:53 JoeLee2017 阅读(410) 评论(0) 编辑 收藏 举报


