动态规划 ------最长公共子序列

这篇博客是我 听完这位老师讲完课的 记录。https://www.youtube.com/watch?v=mgDUoITB24I&t=645s    还有我个人的理解，如果有错误或者有争议的地方，欢迎留言。谢谢大家~

 

子序列  就是说 从原有列表中按照出现先后顺序从中选择部分 元素 组成的新的列表。

 

最长公共子序列的含义：  选择两个列表中公共的子序列的最大长度，这个子序列即为最长公共子序列。

用蛮力的方法求解，对于长度为 M的 列表，它所有的子序列的个数有  2^m  ，每个元素有两种情况，被选入子序列或者不被选入。

 

 

接下来是  动态规划中非常重要的问题，子问题的界定。 对于 长度分别为 M, N的 子列表， 原始的问题是  长度 为 M,N两个子序列的最长子序列，那么，子问题是  对于 长度为M的子序列，我们取 X1到 Xi， 对于长度为 N的子序列，我们取  Y1到 Yj， 那么，由这个子问题界定的范围就是  上图中黄色区域所包括的范围。

在这里，我们看到子问题也有两个参数，一个是代表 x的最后的位置，一个是代表 y的最后的位置。这是两个不同序列的参数。

 

现在考虑 子问题 和  大问题 有着怎么样的依赖关系。 

 

递推方程：

 

注意，我们的目标是 求得最长的公共子序列，所以，当子问题中的两个序列最后的字符不相同，那么，我们就要 裁出  其中的一部分， 同时，要选择 使 子序列长度最大的区间走。

 

标记函数的目标是 追踪我们找到的最长子序列的路径。 我们最开始存的是最长公共子序列的最后那个元素。

 

 

注意： 我们的 C[i,j]存的是  子序列的长度，当  序列X或序列Y的长度为0，那么，最长的公共子序列的长度 C[i,j]当然为0

得到结果后，开始追踪解，也就是获得最长的公共子序列具体是哪些元素。

 

来来来，看老师在课上给的例子。

 

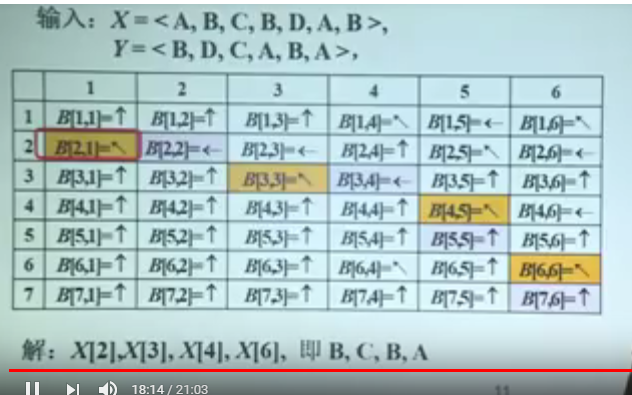
讨论下复杂度。空间+时间

 

 

 

最后老师的总结：

 

 

具体的代码 下次贴咯，在图书馆，窗外下着小雨。学校广播台在放着不知名的音乐，是点歌节目。

 

代码：

 

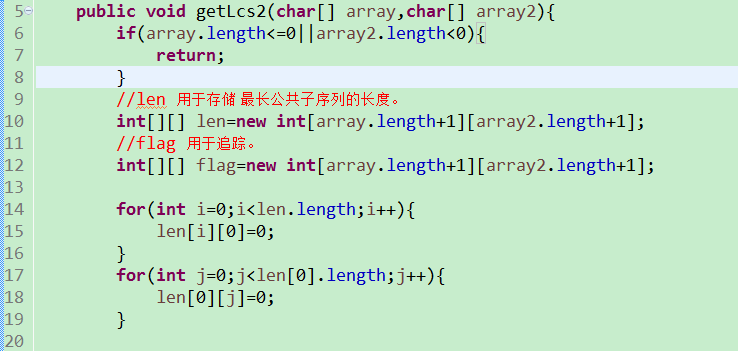
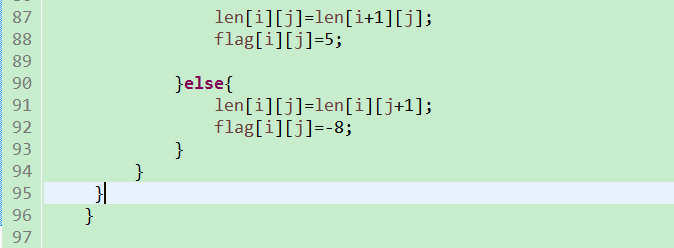
还可以从 底部开始：