人工智能实战2019第三次作业_李大

项目	内容
课程	人工智能实战2019
作业要求	第三次作业
我的课程目标	第一次作业
本次作业作用	熟悉mini_batch的实现、作用

Coding作业

随机选取数据

def GetBatchSamples(X,Y,batch_size,iteration):
    num_feature = X.shape[0]
    shuffled_sequence = np.arange(0, X.shape[1])
    np.random.shuffle(shuffled_sequence)
    batch_x = X[0:num_feature, shuffled_sequence[0: batch_size]].reshape(num_feature, batch_size)
    batch_y = Y[0:num_feature, shuffled_sequence[0: batch_size]].reshape(num_feature, batch_size)
    return batch_x, batch_y

• 重写GetBatchSamples后直接运行即可，每次获取数据时随机产生一个乱序的index list，取前batch size个index作为构造X和Y时使用的索引

取5,10,15的batch_size运行

• max_epoch取50,50,100；eta均取0.1，max_iteration = (int)(num_example / batch_size)
• max_epoch * max_iteration > 800即可，结果比较0=30-800之间loss的变化情况
• GetSampleBatch使用随机获取

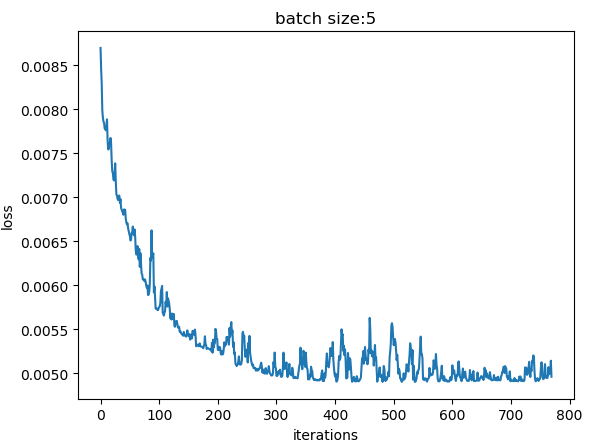
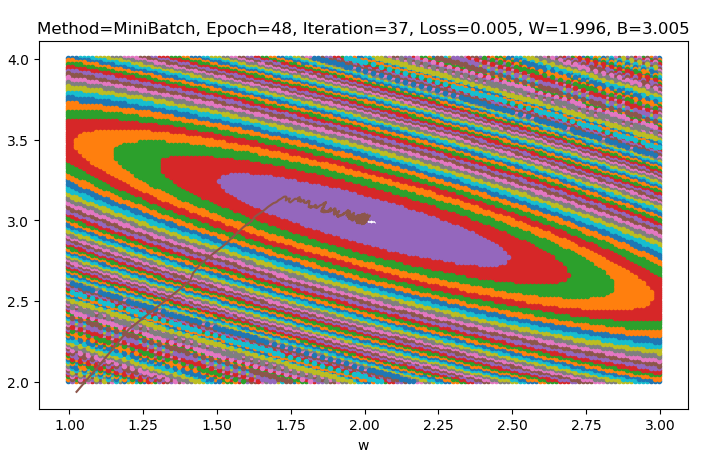
batch_size = 5，总收敛iteration = 48 * (200 / 5) + 37 = 1957

• loss下降曲线抖动明显，抖动源于样本个体的差异

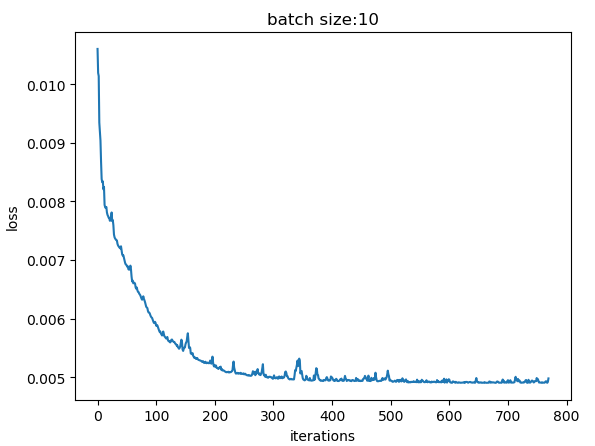
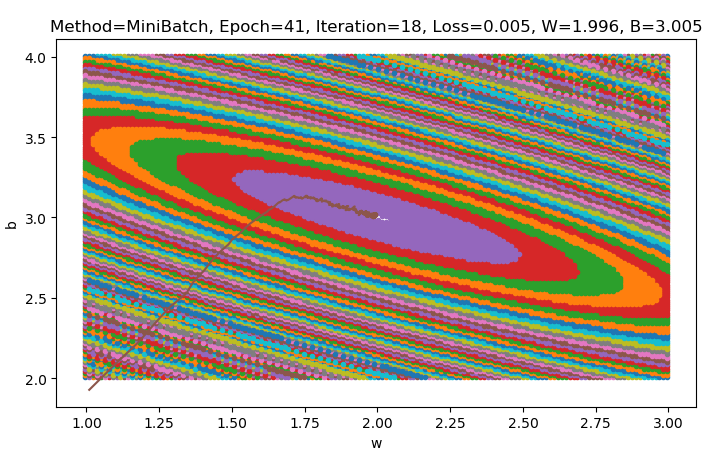
batch_size = 10，总收敛iteration = 41 * 20 + 18 = 838

• 相比batch_size = 5抖动明显减弱很多，更大的batch平均后越能描述样本整体的性质

batch_size = 15，总收敛iteration = 685

• 抖动更不明显

结论：

• batch越大收敛iteration总数越少（但每个iteration的计算量越大），抖动越不明显。大batch更反应样本整体的特性，降低个体样本的噪声。

问题

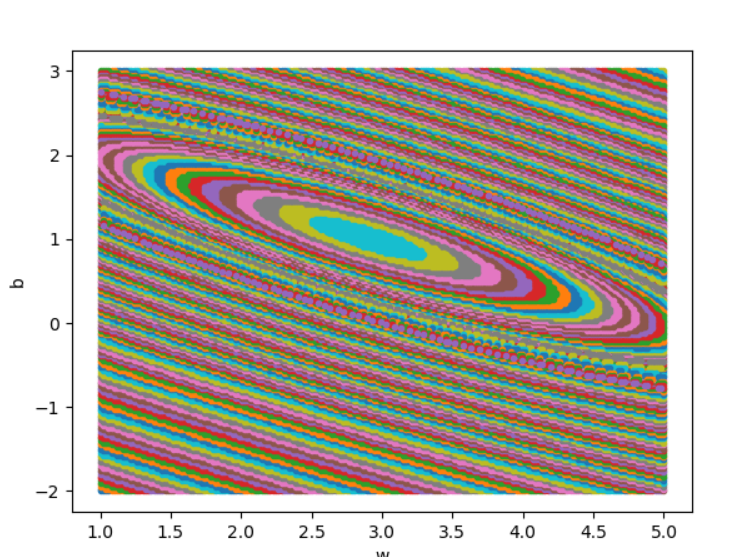
问题2：为什么是椭圆不是圆？如何构造圆图？

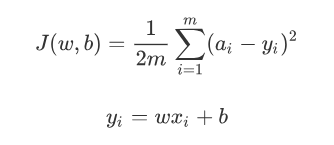
• 上式为均方差损失函数，可以很显然，w和b对J贡献不相等，即J对w和b的偏导数不等的时候J的平面映射图会是椭圆。
• 要想构造平面映射图为圆的损失函数，显然w和b地位对等，可以对换，即可以写成

• 则此时J(w,b) 可写成J1(w)或J1(b)，为圆图

问题3：为什么中心是个椭圆区域而不是一个点？

• 理论上均方差损失函数是有唯一最小值点的，但因为计算机计算时的精度有限，同心椭圆中心处在最小精度以下的数域（都四舍五入为同一个值a）计算结果都只能用一样的损失值（a的损失值）表示，故中心是椭圆区域。
• 据此，计算精度越高，中心的椭圆区域越小。当计算精度无限高（计算时使用无限多位小数时），中心会是一个点。
• 当步长（学习率）无限小时，loss能收敛到中心点。