台阶问题---动态规划算法

问题描述

　　所谓的台阶问题就是说，从0开始上台阶1，2，3...n，每次只能上1个或者2个台阶。问上到n个台阶有多少种走法。这个问题是比较典型的，也有很多种变形，我们先讲解下这种的实现。

 

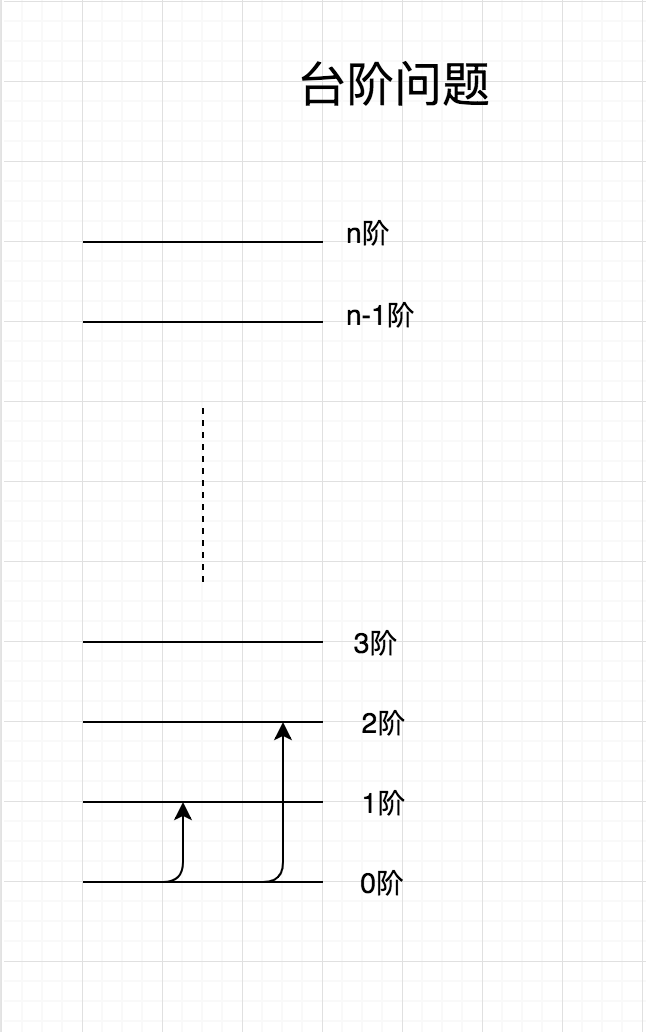
问题分析

　　我们先按照举例来分析，我测试了下，6个台阶时候的变化，如下个表　

台阶数	走法数
1	1
2	2
3	3
4	5
5	8
6	13

这特别像是一个斐波那契数列，那我们想下，如果有10阶台阶，那么我们往后倒推，10阶台阶肯定是第九个台阶和是第八个台阶上来的，那第九个台阶肯定是第八个台阶和第七个台阶上来的，第八个台阶肯定是第七个台阶和第六个台阶上来的，同理，我们得出了f(n)=f(n-1)+f(n-2)  

代码实现

 

 /**
     * 动态规划算法，f(n)=f(n-1)+f(n-2)
     * @param n
     * @return
     */
    private int getSolution(int n){
        if(n < 0){
            return -1;
        }
        if(n == 0){
            return 0;
        }
        if(n == 1){
            return 1;
        }
        int a = 1;
        int b = 1;
        int fn = 0;
        for(int i = 2; i < n+1; i++){
            fn = a + b;
            b = a;
            a = fn;
        }
        return fn;
    }

 

 

问题延伸

　　如果台阶问题变化一下，如果台阶随意可以上，可以上1个，2个，3个.....n个，那么n个台阶的话，有多种走法呢？

　　我们来分析一波，按照上面说的，10个台阶，可以由第九个，八个，七个.......一个台阶都可以上来，那么第九个台阶可以由第八个，七个，六个.....一个台阶都可以上来，同理我们得出，

　　f(n)=f(n-1)+f(n-2)+.......+f(4)+f(3)+f(2)+f(1)

　　f(n-1) = f(n-2) +f(n-3) +........+f(4)+f(3)+f(2)+f(1)

　　经过上面两个算式，我们可以得出，f(n)=2f(n-1)

 　代码实现

 /**
     * 动态规划算法，
     *    f(n)=2f(n-1)
     * @param n
     * @return
     */
    private int getDoubleTree(int n){
        if(n < 0){
            return -1;
        }
        if(n==0){
            return 0;
        }
        if(n==1){
            return 0;
        }
        int a = 1;
        int fn = 0;
        for(int i = 2; i < n + 1; i++){
            fn = 2*a;
            a = fn;
        }
        return fn;
    }