现代精算风险理论10:奖惩系统
第十讲 奖惩系统
第一节 奖惩系统
一、无赔款优待系统简介
汽车保险是非寿险的一个重要分支,在许多国家甚至是总保费收入的最大贡献部分。汽车保险的一个显著特点是保费收取常常极大地依赖于该保单过去的理赔记录,这样的保费收取方式令各方都满意。即投保人会因没有理赔记录而获得奖励,也会因多次理赔记录而受到惩罚。
对于大多数险种而言,风险异质的现象比较普遍。使用某种形式的经验费率使每一种风险的保费率依赖于同种风险的经验赔付水平。至于为什么经验费率在汽车保险中被广泛接受,这里有一个心理上的原因奖励作为对谨慎驾驶员的奖赏,增加的保费作为对易出事故的驾驶员所追加的罪有应得的罚款。
汽车保险中常见的奖惩系统是无赔款优待系统,其英文为 No-Claim Discount,故简记为 NCD。这种计费法就是使用经验费率计算保费的一个应用,其做法是依据驾驶者在上一年的索赔记录来确定其在续保年度时应交的保费。这种保费与实际损失直接挂钩的做法,在一定程度上减少了风险的不均匀性。目前保险市场上实际应用的汽车保险分为交强险和商业险,两者具有不同的 NCD 的体系。
NCD 系统的优点在于:
- NCD 系统有助于减少各费率组别中的风险费均匀性,使保险公司可能收到真实反映单一风险的保费,以致保费相同的一类中的风险尽可能同质;
- NCD 系统可避免小额赔款发生,在降低索赔成本和管理费用的同时,也降低了保费,从而增强了保险人的竞争力;
- NCD 系统可鼓励司机安全行车,对减少交通事故、保持社会安定有促进作用。
构成一个完整的 NCD 系统必须包含三个要素:保费等级;起始组别;转移规则,即依据上一年的索赔记录决定在折扣组别之间转移的规则。
例如:荷兰实行的 NCD 体制共分为 \(14\) 个等级,其折扣规则如表:
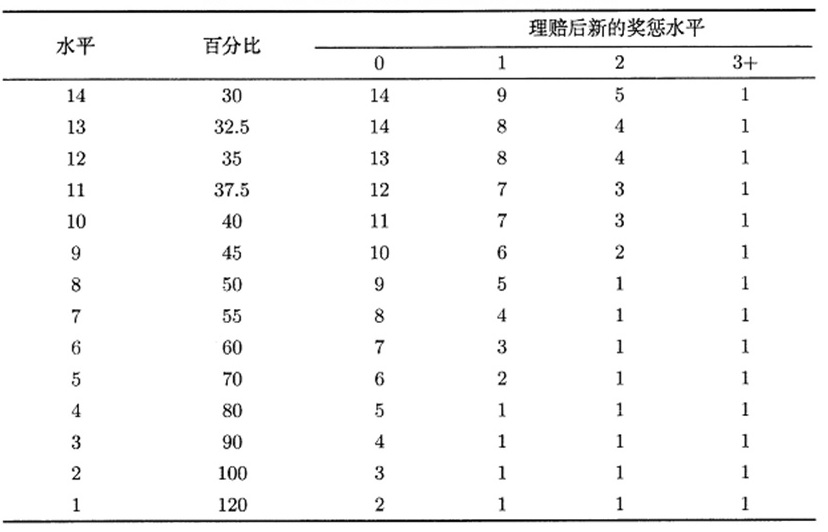
二、马尔可夫分析
这里我们首先回顾一下马尔可夫链中的几个常用的性质和概念:
-
马尔可夫性:指随机过程具有如下的无记忆性,即过程在当前状态的转移概率不依赖于该过程是如何到达这个特定状态的。
-
非周期的马尔可夫链:没有任何一个状态是周期的马尔可夫链。
-
不可约的马尔可夫链:所有状态都可以互达的马尔可夫链。
-
非周期的马尔可夫链必存在极限分布。
-
不可约非周期的具有有限状态马尔可夫链,其极限分布和平稳分布相同且唯一。
奖惩系统可描述为一个马尔可夫链,其转移规则可用转移概率矩阵来描述。以 \(\pi^{(t)}\) 表示时刻 \(t\) 各个组别保单持有人的分布状况,\(P\) 表示转移概率矩阵 \((a_{ij})_{n\times n}\) ,其中 \(a_{ij}\) 表示某一时刻组别 \(i\) 的保单持有人在下一时刻转移到组别 \(j\) 的概率,从而有
令 \(t\to\infty\) ,则在一定的条件下有 \(\pi=\pi P\) ,其中 \(\pi\) 就是保单持有人分布的平稳分布和极限分布。
利用马尔可夫分析可以求出最终处于奖惩系统各个级别上的驾驶员的比例。同时,马尔可夫分析还提供了一种在决定代表驾驶员实际风险的保费调整时,衡量奖惩系统效率的方法。
例如:假设某 NCD 系统由三个折扣组别构成,即 \(0\%\) 、\(25\%\) 和 \(40\%\) ,若年度中无赔案发生,则升至更高折扣组别或停留在 \(40\%\) 折扣组别中。若年度中发生一次或一次以上赔案,则降一级或停留在 \(0\%\) 折扣组别中。计算经过若干期间各折扣组别的人数趋于稳定的比例。
设 \(p_0\) 表示无赔案发生的概率,则由题意知,转移概率矩阵为
\[P=\begin{pmatrix} 1-p_0 & p_0 & 0 \\ 1-p_0 &0 & p_0 \\ 0 & 1-p_0 & p_0 \end{pmatrix}. \]记 \(\pi=\left(\pi_0,\pi_1,\pi_2\right)\) 为保单持有人分布的平稳分布,则由 \(\pi=\pi P\) 可知
\[\left(\pi_0,\pi_1,\pi_2\right)=\left(\pi_0,\pi_1,\pi_2\right) \begin{pmatrix} 1-p_0 & p_0 & 0 \\ 1-p_0 &0 & p_0 \\ 0 & 1-p_0 & p_0 \end{pmatrix}. \]联立 \(\pi_0+\pi_1+\pi_2=1\) ,解方程组可得
\[\pi_0=\frac{(1-p_0)^2}{1-p_0+p_0^2},\quad \pi_1=\frac{p_0(1-p_0)}{1-p_0+p_0^2},\quad \pi_1=\frac{p_0^2}{1-p_0+p_0^2}. \]设 \(p_0=0.9\) 即某险种无赔案发生的概率为 \(0.9\) ,经计算平稳分布为
\[\pi=\left(\frac1{91},\frac{9}{91},\frac{81}{91}\right). \]如果保持无赔案发生的概率为 \(0.9\) ,则经过若干期间各折扣组别的人数将趋于稳定的比例,其中 \(0\%\) 组的占比约为 \(1/91\) ,\(25\%\) 组的占比约为 \(9/91\) ,而 \(40\%\) 组的占比约为 \(81/91\) 。
第二节 奖惩系统对索赔概率的影响
一、奖惩系统可以避免小额赔案的发生
前面的讨论是建立在保单持有人的索赔频率不因其所属的折扣组别不同而不同的基础上展开的。现实生活中,保单持有人在损失小于折扣额时会采用不报案的做法,以风险损失自负来换取折扣额,从而使小额赔案的索赔次数减少。
这里我们主要用例子进行说明。
假设全额保费为 \(500\) 元,保单持有人现处于 \(0\%\) 折扣组别。
如果保单持有人在第一年无索赔发生,假设接下来的年份中无索赔,则将来的保费为 \(375\) 元,\(300\) 元,\(300\) 元,\(\cdots\) 。
如果保单持有人在第一年中发生一次索赔,仍假设接下来的年份中无索赔发生,则将来的保费为 \(500\) 元,\(375\) 元,\(300\) 元,\(300\) 元,\(\cdots\) 。
保单持有人因第一年索赔多支付了 \(200\) 元保费,同样的计算方法可用于其它的折扣组别。
(1) \(0\%\) 组别:临界值 \(200\) 元
\[\begin{array}{l|c|c|c|c|c} \hline & \text{第一年} & \text{第二年} & \text{第三年} & \text{第四年} & \cdots \\ \hline \text{第一年无索赔} & 500 & 375 & 300 & 300 & 300 \\ \text{第一年索赔一次} & 500 & 500 & 375 & 300 & 300 \\ \hline \text{差异} & 0 & 125 & 75 & 0 & 0 \\ \hline \end{array} \](2) \(25\%\) 组别:临界值 \(270\) 元
\[\begin{array}{l|c|c|c|c|c} \hline & \text{第一年} & \text{第二年} & \text{第三年} & \text{第四年} & \cdots \\ \hline \text{第一年无索赔} & 375 & 300 & 300 & 300 & 300 \\ \text{第一年索赔一次} & 375 & 500 & 375 & 300 & 300 \\ \hline \text{差异} & 0 & 200 & 75 & 0 & 0 \\ \hline \end{array} \](3) \(40\%\) 组别:临界值 \(75\) 元
\[\begin{array}{l|c|c|c|c|c} \hline & \text{第一年} & \text{第二年} & \text{第三年} & \text{第四年} & \cdots \\ \hline \text{第一年无索赔} & 300 & 300 & 300 & 300 & 300 \\ \text{第一年索赔一次} & 300 & 375 & 300 & 300 & 300 \\ \hline \text{差异} & 0 & 75 & 0 & 0 & 0 \\ \hline \end{array} \]对于保单持有人而言,如果他目前处于 \(0\%\) ,则只有在损失超过 \(200\) 元的情况下提出索赔才是合算的。
- 假设 \(C\) 为损失额,定义二元变量 \(B\) 和 \(X\) ,其中 \(B\) 为索赔,即 \(B=1\) 索赔发生,\(B=0\) 索赔不发生;\(X\) 为事故,即 \(X=1\) 事故发生,\(X=0\) 事故不发生,于是
\[{\rm Pr}(B=1\mid X=1)={\rm Pr}(C>200). \]
- 索赔的概率为
\[{\rm Pr}(B=1)={\rm Pr}(B=1\mid X=1)\times {\rm Pr}(X=1)<{\rm Pr}(X=1). \]
- 一般来说,\({\rm Pr}(B=1)<{\rm Pr}(X=1)\) ,所以说引入奖惩系统可以避免小额赔案的发生。
二、追逐奖励会导致转移概率矩阵发生改变
追逐奖励:当理赔额小于丧失未来奖金的期望损失时,提请理赔是不明智的,这种现象在实践中被称为追逐奖励,是一类重要的现象。因为被保险人隐瞒了自己是一个差的驾驶员这一事实,所以保险人没有得到应得的保费,但是保险人也从节省了小额理赔的操作费用方面得到了补偿。
我们用下面的例子来说明追逐奖励会导致转移概率矩阵发生改变。
假设 \(C\sim LN(\mu,\sigma^2)\) ,即对数正态分布,并且 \(\mu=5,\sigma=2\) ,其中 \(0\%\) 的临界值 \(200\) 元,\(25\%\) 的临界值为 \(275\) 元,\(40\%\) 的临界值为 \(75\) 元,原无赔案发生的概率 \(p_0=0.9\) 。
\[\begin{aligned} {\rm Pr}(B=1\mid X=1)&={\rm Pr}(C>x) \\ \\ &={\rm Pr}(\ln C>\ln x) \\ \\ &=1-\Phi\left(\frac{\ln x-\mu}{\sigma}\right). \end{aligned} \]于是理赔发生的概率为:
\[\begin{array}{rl} 0\% &\quad 1-\Phi\left(\dfrac{\ln200-6}{2}\right)=1-\Phi(0.149)=0.441 . \\ \\ 25\% &\quad 1-\Phi\left(\dfrac{\ln275-6}{2}\right)=1-\Phi(0.308)=0.379 . \\ \\ 40\% &\quad 1-\Phi\left(\dfrac{\ln75-6}{2}\right)=1-\Phi(0.341)=0.633 . \end{array} \]转移矩阵的变化如下:
\[\begin{array}{rl} 0\%\to 0\% :& 0.441\times0.1=0.0441 , \\ \\ 0\%\to 25\% :& 1-0.0441=0.9559 , \\ \\ 0\%\to 40\% :& 0 , \\ \\ 25\%\to 0\% :& 0.379\times0.1=0.0379 , \\ \\ 25\%\to 25\% :& 0 , \\ \\ 25\%\to 40\% :& 1-0.0379=0.9621 , \\ \\ 40\%\to 0\% :& 0, \\ \\ 40\%\to 25\% :& 0.633\times0.1=0.0633 , \\ \\ 40\%\to 40\% :& 1-0.0633=0.9367 . \end{array} \]所以有
\[P=\begin{pmatrix} 0.1 & 0.9 & 0 \\ 0.1 & 0 & 0.9 \\ 0 & 0.1 & 0.9 \end{pmatrix} \quad \longrightarrow \quad \widetilde{P}=\begin{pmatrix} 0.0441 & 0.9559 & 0 \\ 0.0379 & 0 & 0.9621 \\ 0 & 0.0633 & 0.9367 \end{pmatrix} \]若达到稳定状态,计算平稳分布 / 极限分布,根据 \(\widetilde{\pi}=\widetilde{\pi}\widetilde{P}\) 得到方程组
\[\left\{\begin{array}{l} 0.0441\widetilde{\pi}_0+0.0379\widetilde{\pi}_1=\widetilde{\pi}_0, \\ 0.9559\widetilde{\pi}_0+0.0633\widetilde{\pi}_2=\widetilde{\pi}_1, \\ 0.9621\widetilde{\pi}_1+0.9631\widetilde{\pi}_2=\widetilde{\pi}_2, \\ \widetilde{\pi}_0+\widetilde{\pi}_1+\widetilde{\pi}_2=1 . \end{array}\right. \]解得新的平稳分布为
\[\widetilde{\pi}_0=0.0024 , \quad \widetilde{\pi}_1=0.0616 , \quad \widetilde{\pi}_2=0.9360. \]对比有奖励和没有奖励的两种情况:
\[\begin{array}{l} &\pi_0=\dfrac1{91}=0.011 \quad \longrightarrow \quad \widetilde{\pi}_0=0.0024 \quad \text{(概率下降)} \\ \\ &\pi_1=\dfrac9{91}=0.099 \quad \longrightarrow \quad \widetilde{\pi}_1=0.0616 \quad \text{(概率下降)} \\ \\ &\pi_2=\dfrac{81}{91}=0.890 \quad \longrightarrow \quad \widetilde{\pi}_2=0.9360 \quad \text{(概率上升)} \end{array} \]由于对无索赔奖励的追逐,在第一组 \(0\%\) 和第二组 \(25\%\) 的人的比例小了,而第三组 \(40\%\) 的人的比例增加了。
由于保单持有人选择大于折扣额的损失额进行索赔,因而最终导致高折扣额组别的保单数比重增加,从而导致总体保费下降。
三、平均保费水平
由于奖惩系统的调整作用,保单组合的平均保费水平在最初的若干年会不断发生变化,直到奖惩系统进入平稳状态。
假设无索赔概率 \(p_0=0.9\) ,并令第一年均以 \(0\%\) 状态进入,即初始状态为 \((1,0,0)\) ,因此第一年的平均保费水平为 \(P=1\) 。
第二年的分布为 \((0.1,0.9,0)\) ,此时的平均保费水平为
\[P=1\times0.1+0.75\times0.9=0.775. \]如果不考虑追逐奖励,进入平稳状态后,各组的人数比例为\(\left(\frac1{91},\frac{9}{91},\frac{81}{91}\right)\) ,此时的平均保费水平为
\[P=\frac1{91}\times1+\frac{9}{91}\times0.75+\frac{81}{91}\times0.6=0.619. \]如果考虑追逐奖励,即考虑奖惩系统可避免小额赔偿的发生,进入平稳状态后,各组的人数比例为 \((0.0024,0.0616,0.9360)\) ,此时的平均保费水平为
\[P=0.0024\times1+0.0616\times0.75+0.9360\times0.6=0.610. \]
第三节 奖惩系统的评价
奖惩系统的最终目标是使每个投保人所支付的保费尽可能准确地反映其年理赔额的期望值。
对于奖惩系统的比较,既可从保单持有人的角度进行,也可以从保险公司角度进行,选择不同的角度,就有截然不同的结果。下面介绍两个评价标准是从保单持有人的角度出发,它们从不同方面反映了一个奖惩系统对保单持有人的奖惩来历程度。
(1) 稳定状态下的相对平均保费水平 \(\text{RSAL}\)
当奖惩系统进入稳定状态时,保单持有人在奖惩系统中的位置进行度量,反映了保单持有人在奖惩系统的最低保费等组中的聚集程度,其定义式为
较低的 \({\rm RSAL}\) 值表明大多数保单集中在了最高的保费折扣等级,反之则保单集中在了较低的保费折扣等级,一般理想的值为 \(50\%\) 左右。
在上述例子中,不考虑追逐奖励,则有
\[\text{RSAL}=\frac{0.619-0.6}{1.0-0.6}=0.475. \]
(2) 奖惩系统的弹性
奖惩系统的弹性度量了奖惩系统对索赔频率的变化所能做出的反应。理论上,一个合理的奖惩系统,保单持有人在一生中所缴纳的保费应该是索赔概率的线性增函数。
假设有两个保单持有人,一个的索赔概率为 \(0.10\) ,另一个的索赔额为 \(0.11\) 。如果经过较大的一段时间以后,第二个保单持有人比第一个多缴纳 \(10\%\) ,则次奖惩系统被认为是具有完全弹性的。
如果保险费的增量 \(2\%\) ,则奖惩系统的弹性被认为是 \(20\%\) 。然而,事实上大多数情形下保费增量远远不及 \(10\%\) 。
在上述例子中,如果 \(p_0=0.11\) ,则平稳分布为 \((0.0134,0.1085,0.8781)\) ,平均保费水平为
\[P=1\times0.0134+0.75\times1085+0.8781\times0.6=0.622. \]和原来的 \(0.619\) 相比较增加
\[\frac{0.622-0.619}{0.619}=0.485\%. \]保费增量远远没有达到 \(10\%\) 的水平。


