现代精算风险理论09：破产概率(2)

目录

• 第九讲 破产概率(2)
  • 第四节 破产概率的表达式
    • 一、盈余过程的性质
    • 二、连续时间模型的破产概率
    • 三、离散时间模型的破产概率
    • 四、再保险与破产概率
  • 第五节 Beekman卷积公式
    • 一、创新下纪录
    • 二、破产时刻资本金的分布
    • 三、破产概率的解析表达式

第九讲 破产概率(2)

第四节 破产概率的表达式

一、盈余过程的性质

在一定条件下，我们希望能够给出破产概率的一个准确表达式。

• 对于一般的理赔分布，该表达式涉及到 \(U(t)\) 在给定破产发生在有限时间条件下的矩母函数。
• 在指数型理赔下，我们可以给出破产概率的一个准确表达式。

在此之前，我们先对盈余过程 \(U(t)\) 和总索赔过程 \(S(t)\) 的性质展开进一步讨论。

定理：在盈余过程的定义中，盈余过程有如下的假设：

• 假设 1：假设 \(N(t)\) 是参数为 \(\lambda\) 的泊松过程；
• 假设 2：假设所有的索赔额 \(X_i\) 相互独立同分布；
• 假设 3：索赔额 \(X_i\) 与 \(N(t)\) 相互独立。

由上面三个假设可以得出总索赔过程 \(S(t)\) 具有独立增量性和平稳增量性。相应的，盈余过程 \(U(t)\) 也具有独立增量性和平稳增量性。

总索赔过程的定义为

\[S(t)=\sum_{i=1}^{N(t)}X_i. \]

独立增量性：对于 \(\forall s<t\) ，都有

\[S(s)=\sum_{i=1}^{N(s)}X_i,\quad S(t)-S(s)=\sum_{i=1}^{N(t)}X_i-\sum_{i=1}^{N(s)}X_i=\sum_{i=N(s)+1}^{N(t)}X_i. \]

显然 \(S(s)\) 与 \(S(t)-S(s)\) 相互独立。

平稳增量性：对于 \(\forall s<t\) ，都有

\[S(t)-S(s)=\sum_{i=N(s)+1}^{N(t)}X_i,\quad S(t-s)=\sum_{i=1}^{N(t-s)}X_i. \]

由泊松过程的平稳增量性，即 \(N(t-s)\xlongequal{d}N(t)-N(s)\) ，所以 \(S(t-s)\xlongequal{d}S(t)-S(s)\) 。

注意到，随机过程 \(e^{-RU(t)}\) 满足如下两个性质，即 \(e^{-RU(t)}\) 是一个鞅：

(1) 对 \(\forall t\geq0\) ，都有

\[\begin{aligned} \mathbb{E}\left[e^{-RU(t)}\right]&=\mathbb{E}\left[e^{-R(u+ct-S(t))}\right]=e^{-Ru}e^{-Rct}e^{\lambda t\left(m_X(R)-1\right)}=e^{-Ru}. \end{aligned} \]

(2) 记 \(\mathcal{F}_s=\sigma\{S(s),s\geq0\}\) ，对于 \(\forall s\leq t\) ，有

\[\begin{aligned} \mathbb{E}\left[e^{-RU(t)}\big|\mathcal{F}_s\right]&=\mathbb{E}\left[e^{-R(u+ct-S(t))}\big|\mathcal{F}_s\right] \\ \\ &=e^{-R(u+ct)}\mathbb{E}\left[e^{RS(t)}\big|\mathcal{F}_s\right] \\ \\ &=e^{-R(u+cs-S(s))}\mathbb{E}\left[e^{R(S(t)-S(s))}\right]e^{-Rc(t-s)} \\ \\ &=e^{-RU(s)}. \end{aligned} \]

事实上，随机过程 \(e^{-RU(t)}\) 的两个性质，分别刻画了 \(U(t)\) 在无条件下和在给定破产发生在有限时间条件下的的矩母函数。在此基础上，我们可以给出破产概率的一个准确的表达式。

二、连续时间模型的破产概率

定理：设初始资本金 \(u\geq0\) ，则破产概率满足

\[\psi(u)=\frac{e^{-Ru}}{\mathbb{E}\left[e^{-RU(t)}\big|T<\infty\right]}. \]

对 \(R>0\) 和 \(t>0\) ，有

\[\begin{aligned} \mathbb{E}\left[e^{-RU(t)}\right]&=\mathbb{E}\left[e^{-RU(t)}\big|T\leq t\right]{\rm Pr}(T\leq t)+\mathbb{E}\left[e^{-RU(t)}\big|T>t\right]{\rm Pr}(T> t) \\ \\ &\xlongequal{def}I_1+I_2. \end{aligned} \]

对 \(\forall v\in[0,t]\) ，有 \(U(t)=U(v)-c(t-v)-[S(t)-S(v)]\) ，则有

\[\begin{aligned} \mathbb{E}\left[e^{-RU(t)}\big|T=v\right]&=\mathbb{E}\left[e^{-R[U(v)-c(t-v)-[S(t)-S(v)]]}\big|T=v\right] \\ \\ &=\mathbb{E}\left[e^{-RU(v)}\big|T=v\right]e^{-Rc(t-v)}\mathbb{E}\left[e^{-R[S(t)-S(v)]}\big|T=v\right] \\ \\ &=\mathbb{E}\left[e^{-RU(v)}\big|T=v\right]\left[e^{-Rc}\exp\left\{\lambda(m_X(R)-1)\right\}\right]^{t-v} \\ \\ &=\mathbb{E}\left[e^{-RU(T)}\big|T=v\right]. \end{aligned} \]

上述证明过程中用到了以下的性质：

• 发生在 \(v\) 和 \(t\) 之间的理赔总额 \(S(t)-S(v)\) 还是服从复合泊松分布，且与 \(S(t-v)\) 同分布；
• 因为风险过程在 \(v\) 之后的情况独立于在 \(v\) 之前的情况，所以 \(U(v)\) 与 \(S(t)-S(v)\) 相互独立。
• 由调节系数方程可知，\(e^{-Rc}\exp\left\{\lambda(m_X(R)-1)\right\}=1\) 。

由上面的等式可知，对所有的 \(v\leq t\) 成立，所以

\[\mathbb{E}\left[e^{-RU(t)}\big|T\leq v\right]=\mathbb{E}\left[e^{-RU(T)}\big|T\leq v\right]=\mathbb{E}\left[e^{-RU(T)}\big|T\leq t\right]. \]

所以 \(I_1\) 的部分，对所有的 \(v\leq t\) 都有

\[I_1=\mathbb{E}\left[e^{-RU(T)}\big|T\leq t\right]{\rm Pr}(T\leq t). \]

因为当 \(t\to\infty\) 时，有

\[{\rm Pr}(T\leq t) \uparrow {\rm Pr}(T < \infty) , \]

所以当 \(t\to\infty\) 时，有

\[I_1\to \mathbb{E}\left[e^{-RU(T)}\big|T<\infty \right]{\rm Pr}(T<\infty). \]

接下来只需证当 \(t\to\infty\) 时，有

\[I_2=\mathbb{E}\left[e^{-RU(t)}\big|T>t\right]{\rm Pr}(T> t) \to0. \]

注意到 \(T>t\) 意味着保险公司在时刻 \(t\) 没有破产，即 \(U(t)>0\) ，所以 \(e^{-RU(t)}\leq 1\) 。

下面分两种情况来讨论，对于某个函数 \(u_0(t)\) ，分别考虑 \(U(t)\leq u_0(t)\) 和 \(U(t)>u_0(t)\) 的情况。

\[\begin{aligned} I_2&=\mathbb{E}\left[e^{-RU(t)}\mid T>t\right]{\rm Pr}(T> t) \\ \\ &=\mathbb{E}\left[e^{-RU(t)}\mid T>t,0\leq U(t)\leq u_0(t)\right]{\rm Pr}\left[T> t,0\leq U(t)\leq u_0(t)\right] \\ \\ &\quad \; +\; \mathbb{E}\left[e^{-RU(t)}\mid T>t,U(t)> u_0(t)\right]{\rm Pr}\left[T> t,U(t)> u_0(t)\right] \\ \\ &\leq {\rm Pr}\left[U(t)\leq u_0(t)\right] + \mathbb{E}\left[e^{-Ru_0(t)}\right] \\ \\ &\xlongequal{def}I_{21}+I_{22}. \end{aligned} \]

取 \(u_0(t)=t^{2/3}\) ，则当 \(t\to\infty\) 时，有 \(u_0(t)\to\infty\) ，从而 \(I_{22}=\mathbb{E}\left[e^{-Ru_0(t)}\right]\to0\) 。

考虑 \(I_{21}\) 项，注意到：

• \(U(t)\) 的期望为 \(\mathbb{E}\left[U(t)\right]=u+ct-\lambda t\mu_1\) ；
• \(U(t)\) 的方差为 \({\rm Var}[U(t)]=\lambda t(\sigma^2+\mu_1^2)=\lambda t\mu_2\) 。

当 \(t\) 充分大时，有 \(u_0(t)-(u+ct-\lambda t\mu_1)<0\) ，所以

\[\begin{aligned} I_{21}&={\rm Pr}\left[U(t)\leq u_0(t)\right] \\ \\ &={\rm Pr}\left[U(t)-\mathbb{E}[U(t)]\leq u_0(t)-(u+ct-\lambda t\mu_1)\right] \\ \\ &\leq {\rm Pr}\left[U(t)-\mathbb{E}[U(t)]\geq \left|u_0(t)-(u+ct-\lambda t\mu_1)\right|\right] \\ \\ &\leq \frac{{\rm Var}[U(t)]}{\left[ u_0(t)-(u+ct-\lambda t\mu_1)\right]^2} \\ \\ &= \frac{\lambda t\mu_2}{\left[ u_0(t)-(u+ct-\lambda t\mu_1)\right]^2} \to 0 \quad (t\to\infty). \end{aligned} \]

故破产概率的表达式证毕。

推论：由破产概率满足的表达式可以推出以下结论：

\[\psi(u)=\frac{e^{-Ru}}{\mathbb{E}\left[e^{-RU(t)}\big|T<\infty\right]}. \]

1. 如果 \(\theta\downarrow 0\) ，则 \(\psi(u)\to1\) ，即破产概率趋于 \(1\) 。

   因为 \(\theta\downarrow 0\) ，则有 \(R\downarrow 0\) ，从而有 \(e^{-Ru}\to1\) 和 \(e^{-RU(t)}\to1\) ，故 \(\psi(u)\to1\) 。

2. 如果 \(T<\infty\) ，则 \(U(T)<0\) ，从而有 \(\psi(u)\leq e^{-Ru}\) 。

3. 如果理赔额不超过 \(b\) ，则 \(U(T)\geq -b\) ，由此可以得到破产概率的一个指数型下界：

   \[\psi(u)\geq e^{-R(u+b)}. \]

4. 当 \(u\to\infty\) 时，破产概率的分布有一个有限的极限，设此极限为 \(c\) ，于是有 \(c>1\) 。由此可得如下的关于破产概率的渐近逼近公式，当 \(u\) 取大值时，有

   \[\psi(u)\approx \frac1c e^{-Ru}. \]

5. 如果 \(R>0\) ，那么对任何的 \(u\geq 0\) 有 \(1-\psi(u)>0\) 。

6. 如果 \(\exists u_0\geq0\) ，有 \(1-\psi(u_0)=0\) ，则 \(R=0\) ，且对 \(\forall u\geq0\) 有 \(1-\psi(u)=0\) 成立。

例如（指数型理赔）：当理赔额 \(X\sim Exp(\beta)\) 时，我们可以推导出破产概率的准确表达式。

设破产发生在有限时刻，且破产前的最后一刻资金 \(U(T-0)=v>0\) ，即

\[U(T)=U(T-0)-X, \]

其中 \(X\) 是破产时刻的索赔。

如果 \(H\) 表示满足 \(U(T-0)=v\) 时，在 \(T\) 时刻破产发生，即 \(U(T)<0\) ，或 \(X>v\) ，则有

\[{\rm Pr}\left[-U(T)>y\mid H\right]={\rm Pr}\left[X>v+y\mid X>v\right]=\frac{e^{-\beta(v+y)}}{e^{-\beta v}}=e^{-\beta y}. \]

所以破产时刻的亏损 \(-U(T)\) 也服从一个参数为 \(\beta\) 的指数分布，所以

\[\mathbb{E}\left[e^{-RU(T)}\mid T<\infty\right]=\frac{\beta}{\beta-R}. \]

由 \(\beta=1/\mu_1\) 和 \(R=\theta\beta/(1+\theta)\) 可知

\[\frac{\beta}{\beta-R}=1+\theta. \]

所以当理赔额 \(X\sim Exp(\beta)\) 时，可以得到破产概率的准确表达式

\[\begin{aligned} \psi(u)&=\frac{1}{1+\theta}\exp\left\{-\frac{\theta\beta u}{1+\theta}\right\} \\ \\ &=\frac{1}{1+\theta}\exp\left\{-\frac{\theta}{1+\theta}\frac{u}{\mu_1}\right\} \\ \\ &=\psi(0)e^{-Ru}. \end{aligned} \]

三、离散时间模型的破产概率

在离散时间模型中，我们考虑风险过程 \(U(t)\) 在 \(t=0,1,2,\cdots\) 时刻处的取值，风险模型可以写为

\[U(n)=u+cn-\sum_{i=1}^{n}S_i,\quad n=0,1,2,\cdots, \]

其中，时刻 \(n\) 的总索赔为

\[S_n=\sum_{i=1}^{N(n)-N(n-1)}X_i\xlongequal{d}\sum_{i=1}^{N(1)}X_i. \]

令 \(G_n=c-S_n\) 表示从 \(n-1\) 到 \(n\) 时间段的总收益，即保费收入减去索赔总额，则风险模型为

\[U(n)=u+\sum_{i=1}^nG_i, \quad n=0,1,2,\cdots. \]

假设 \(G_1,G_2,\cdots\) 是独立同分布的，满足 \({\rm Pr}(G_n<0)>0\) 和 \(\mathbb{E}[G_n]=\mu>0\) ，则离散时间模型中的破产时间和破产概率可以重新定义为

\[\widetilde{T}(u)=\min\{n\geq1:U(n)< 0\}, \\ \\ \widetilde\psi(u)={\rm Pr}\left[\widetilde{T}(u)<\infty\right]. \]

调节系数 \(\widetilde{R}>0\) 为如下方程的解：

\[m_G\left(-r\right)=\mathbb{E}\left[e^{-Gr}\right]=1. \]

上述方程有唯一解，其中 \(G\) 的分布为

\[G\xlongequal{d}c-\sum_{i=1}^{N(1)}X_i. \]

可以推出调节系数方程的等价形式：

\[\begin{aligned} \mathbb{E}\left[e^{-G\widetilde{R}}\right]=1 \quad &\Longrightarrow \quad \mathbb{E}\left[e^{-\widetilde{R}\left(c-\sum_{i=1}^{N(1)}X_i\right)}\right]=1 \\ \\ &\Longrightarrow \quad \mathbb{E}\left[e^{\widetilde{R}\left(\sum_{i=1}^{N(1)}X_i\right)}\right]=e^{Rc}. \end{aligned} \]

四、再保险与破产概率

在前面的讨论中，再保险合同的优劣是通过期望效用进行比较的。事实上，再保险合同的优劣还可以通过再保险后的破产概率的大小进行比较。

和破产概率相关的，将尝试通过调节系数来选择最优再保险，即在调节系数 \(R\) 大于某个 \(R_0\) 的限制条件下最大化期望收益。这是因为，在一般情况下，调节系数 \(R\) 越大，破产概率 \(\psi(u)\) 越小；而调节系数 \(R\) 越小，破产概率 \(\psi(u)\) 越大。这里我们将主要考虑两种情形：

• 使用离散时间破产模型，剔除一年理赔总额的再保份额，再比较离散调节系数 \(R\) ；
• 使用连续时间破产模型，在两种形式的再保险（即比例再保险和超额损失再保险）下比较 \(R\) 。

首先给出一个离散时间破产模型的例子：

例如（离散化的复合泊松理赔过程）：考虑参数 \(\lambda=1\) 的复合泊松分布，索赔 \(X_i\) 服从两点分布

\[p(1)=p(2)=\frac12,\quad \mu_X=1.5. \]

如果相对安全附加系数为 \(\theta=0.2\) ，即年保费 \(c=(1+\theta)\mu_X=1.8\)

(1) 首先写出离散的盈余过程：

\[U(n)=u+cn-\sum_{k=1}^nS_k, \]

其中 \(S_k\) 独立同分布，可以写为

\[S_k=\sum_{i=1}^{N(1)}X_i, \quad \mathbb{E}[S_k]=\lambda\mu_X=1.5. \]

(2) 假设 \(S\) 与 \(S_k\) 同分布，则计算一年的总理赔 \(S\) 的离散调节系数 \(\widetilde{R}\) 如下：

\[\lambda+cr=\lambda m_X(r) \quad \Longrightarrow \quad 1+1.8r=\frac12e^r+\frac12e^{2r} \quad \Longrightarrow \quad \widetilde{R}\approx 0.211. \]

也可以直接利用离散调节系数方程求解，设 \(G=c-S\) ，则

\[m_S(r)=m_{N}(\log m_X(r) )=\exp\left\{\lambda(m_X(r)-1)\right\}=\exp\left\{\frac12e^r+\frac12e^{2r}-1\right\}. \]

所以

\[m_G(-r)=\mathbb{E}\left[e^{-rG}\right]=\mathbb{E}\left[e^{-r(c-S)}\right]=e^{-rc}m_S(r)=\exp\left\{\frac12e^r+\frac12e^{2r}-1-1.8r\right\}. \]

令 \(m_G(-r)=1\) 可以得到上述同样的结果 \(\widetilde{R}\approx0.211\) 。

(3) 考虑再保险的情形，假设取自留额 \(d=3\) 的停止损失再保险，再保险保费采用均值保费原理计算，即对于一个理赔 \(Y\) ，再保险公司索要的保费是 \((1+\rho)\mathbb{E}(Y)\) ，其中取 \(\rho=0.8\) ，此时的盈余过程是

\[U(n)=u+cn-n\Pi[d]-\sum_{k=1}^n\min\{S_i,d\}, \]

其中

\[\Pi[d]=(1+\rho)\mathbb{E}[S_i-d]_+,\quad c=(1+\theta)\mathbb{E}(S_i). \]

(4) 计算再保险保费，当 \(d=3\) 时，由 Panjer 递推可得

\[\mathbb{E}[S-3]_+=0.201. \]

所以再保险保费相当于

\[\Pi[d]=(1+\rho)\mathbb{E}[S-d]_+=1.8\times0.201=0.362. \]

(5) 一年的总收益为 \(G_i=c-\Pi[d]-\min\{S_i,d\}\) ，即

\[\begin{aligned} G_i&=1.8-\Pi[3]-\min\{S_i,3\} \\ \\ &=\left\{\begin{array}{ll} 1.8-0.362-S_i , & S_i=0,1,2,3 , \\ \\ 1.8-0.362-3 , & S_i\geq4. \end{array}\right. \end{aligned} \]

即盈余过程可以改写为

\[U(n)=u+\sum_{i=1}^nG_i. \]

(6) 由 \(G_i\) 独立同分布，假设与 \(G\) 有相同的分布，对应的离散调节系数 \(\widetilde{R}\) 由 \(m_G(-r)=1\) 解出

\[\begin{aligned} \mathbb{E}\left[e^{-rG}\right]&=\sum_{k=0}^3\mathbb{E}\left[e^{-rG}\mid S=k\right]{\rm Pr}(S=k)+\mathbb{E}\left[e^{-rG}\mid S\geq4\right]{\rm Pr}(S\geq4) \\ \\ &=e^{-1.438r}\times\left[0.368+0.184e^r+0.23e^{2r}+0.099e^{3r}\right]+0.119e^{1.562r}. \end{aligned} \]

令 \(\mathbb{E}\left[e^{-rG}\right]=1\) ，用数值逼近的方法得出近似值为 \(\widetilde{R}\approx0.199\) 。

(7) 由于再保险，期望年收益减少了，等于我们最初的期望收益再减去再保险公司的收益。

当 \(d=3\) 时，收益为

\[\begin{aligned} \mathbb{E}(G_i)&=1.8-\Pi[3]-\mathbb{E}\left[\min\{S_i,3\}\right] \\ \\ &=1.8-0.362-(1.5-0.201) \\ \\ &=0.139. \end{aligned} \]

(8) 下表给出了不同自留额 \(d\) 对应的一些结果

\[\begin{array}{ccc} \hline d & \widetilde{R}& \mathbb{E}(G_i) \\ \hline 3 & 0.199 & 0.139 \\ 4 & 0.236 & 0.234 \\ 5 & 0.230 & 0.273 \\ \infty & 0.211 & 0.300 \\ \hline \end{array} \]

说明 \(d=3\) 这个决策是不合理的，和没有再保险 \((d=∞)\) 相比较，再保险后，期望收益减少，而且调节系数也变小了，即破产概率变大了。而 \(d=4,d=5\) 的决策比较好，再保险后，虽然期望收益下降了，但调节系数变大了，即破产概率变小了。

接下来给出一个连续时间破产模型的例子，并且考虑比例再保险和超额损失再保险两个特例。

例如（个体理赔的再保险问题）：对于每个理赔 \(X_j\) ，考虑再保险之后的赔付额为 \(h(X_j)\) ，自留损失为 \(X_j-h(X_j)\) ，考虑以下两种再保险函数：

1. 比例再保险：\(h(x)=\alpha x, \ 0\leq \alpha \leq 1\) ；
2. 超额损失再保险：\(h(x)=(x-\beta)_+,\ \beta\geq0\) 。

(1) 首先写出连续的盈余过程：

\[U(t)=u+(c-c_h)t-\sum_{j=1}^{N(t)}\left[X_j-h(X_j)\right], \]

其中 \(c_h=(1+\rho)\lambda\mathbb{E}\left[h(X_j)\right]\) ，可以由下式计算得到：

\[c_ht=\Pi\left[\sum_{j=1}^{N(t)}h(X_j)\right]=(1+\rho)\lambda\mathbb{E}\left[h(X_j)\right]t. \]

(2) 由调节系数方程，我们有

\[\lambda+(c-c_h)r=\lambda m_{X-h(X)}(r), \\ \\ \lambda+(c-c_h)r=\lambda\int_0^\infty e^{r(x-h(x))}{\rm d}F(x). \]

(3) 假设再保险保费采用均值保费原理计算，即 \(c_h=(1+\rho)\lambda\mathbb{E}\left[h(X)\right]\) ，则方程为

\[\lambda+(1+\theta)\lambda\mathbb{E}\left(X\right)r-c_h r=\lambda\int_0^\infty e^{r(x-h(x))}{\rm d}F(x). \]

(4) 进一步假设：泊松强度 \(\lambda=1\) ，安全符合系数为 \(\theta=1/3\) ，索赔 \(X\) 的分布为

\[p(1)=p(2)=\frac12, \]

则有 \(c=(1+\theta)\lambda\mathbb{E}(X)=2\) ，相应的方程为

\[\lambda+2r-(1+\rho)\mathbb{E}\left[h(X)\right]r=\lambda\int_0^\infty e^{r(x-h(x))}{\rm d}F(x). \]

(5) 考虑两个值，分别讨论比例再保险后盈余过程的调节系数：

\[\rho=\frac13, \quad\text{ or }\quad \rho=\frac25. \]

对于比例再保险 \(h(x)=\alpha x\) ，保费等于

\[c_h=(1+\rho)\lambda\mathbb{E}\left[h(X)\right]=(1+\rho)\frac32\alpha. \]

由于 \(x-h(x)=(1-\alpha)x\) ，故调节系数满足方程

\[1+\left[2-(1+\rho)\frac32\alpha\right]r=\frac12e^{r(1-\alpha)}+\frac12 e^{2r(1-\alpha)}. \]

当 \(\rho=1/3\) 时，则有 \(c_h=2\alpha\) ，\(R_h=0.325/(1-\alpha)\) 。

当 \(\rho=2/5\) 时，则有 \(c_h=2.1\alpha\) ，\(R_h\) 可通过插值的方法给出数值解。

表中给出对应于不同的 \(\alpha\) 值的 \(R_h\) 的结果：

\[\begin{array}{c|c|c|c|c|c|c|c} \hline & \alpha & 0.0 & 0.2 & 0.4 & 0.6 & 0.8 & 0.9 & 1.0 \\ \hline \rho=\dfrac13 & R_h & 0.326 & 0.407 & 0.542 & 0.813 & 1.63 & 3.25 & \infty \\ \hline \rho=\dfrac25 & R_h & 0.326 & 0.390 & 0.482 & 0.602 & 0.382 & \\ \hline \end{array} \]

当 \(\rho=1/3\) 时，再保险公司和保险人的相对安全附加系数相等，办理的再保险越多，调节系数就越大。

当 \(\rho=2/5\) 时，对于 \(\alpha\geq5/6\) ，自留损失的期望为

\[\mathbb{E}\left[X-h(X)\right]=\frac32(1-\alpha)>c-c_h=2-2.1\alpha, \]

根据前面的讨论可知，自留安全系数不是正数，而且最终破产是必然的。

(6) 考虑两个值，分别讨论超额损失再保险后盈余过程的调节系数：

\[\rho=\frac13, \quad\text{ or }\quad \rho=\frac25. \]

对于超额损失再保险 \(h(x)=(x-\beta)_+,\ 0\leq \beta\leq 2\) ，保费等于

\[c_h=(1+\rho)\lambda\mathbb{E}\left[h(X)\right]=\frac12(1+\rho)\left[(1-\beta)_++(2-\beta)_+\right]. \]

由于 \(x-h(x)=\min\{x,\beta\}\) ，故调节系数满足方程

\[1+\left[2-\frac12(1+\rho)\left[(1-\beta)_++(2-\beta)_+\right]\right]r=\frac12\left[e^{\min\{\beta,1\}r}+e^{\min\{\beta,2\}r}\right]. \]

表中给出对应于不同的 \(\beta\) 值的 \(R_h\) 的结果：

\[\begin{array}{c|c|c|c|c|c|c|c} \hline & \beta & 2.0 & 1.4 & 0.9 & 0.6 & 0.3 & 0.15 & 0.0 \\ \hline \rho=\dfrac13 & R_h & 0.326 & 0.443 & 0.612 & 0.918 & 1.84 & 3.67 & \infty \\ \hline \rho=\dfrac25 & R_h & 0.326 & 0.426 & 0.541 & 0.667 & 0.425 & \\ \hline \end{array} \]

当 \(\rho=1/3\) 时，再保险公司和保险人的相对安全附加系数相等，办理的再保险越多，调节系数就越大。

当 \(\rho=2/5\) 时，对于 \(\beta\leq1/4\) ，自留损失的期望不再小于剩余自留保费，因此自留安全系数不是正数，最终破产是必然的。

第五节 Beekman卷积公式

一、创新下纪录

本节我们主要研究未破产概率 \(1-\psi(u)\) 的表达式，这里我们将证明未破产概率可以表示为一个复合集合分布的分布函数。

考虑最大累计损失，即到 \(t\) 时刻为止的总理赔额和收取保费的差的最大值：

\[L=\max\{S(t)-ct\mid t\geq0\}. \]

因为 \(S(0)=0\) ，所以 \(L\geq0\) ，事件 \(L>u\) 发生当且仅当存在一个有限时刻 \(t\) ，使得 \(U(t)<0\) ，所以事件 \(L>u\) 和 \(T<\infty\) 是等价的，从而有

\[\psi(u)=1-F_L(u). \]

考虑盈余过程创新下纪录的时刻，这必然发生在有理赔支付的时刻。用随机变量 \(\{L_j,j=1,2,\cdots\}\) 表示第 \(j\) 个创新下纪录小于第 \(j-1\) 个创新下纪录的量，设 \(M\) 是新纪录的随机个数，则有

\[L=L_1+L_2+\cdots+L_M. \]

例如，图中共画出了 \(3\) 个创新下纪录的点，分别发生在 \(T_1,T_2\) 和 \(T_4\) 时刻，其中 \(T_4\) 即为破产时刻，并且图中表示出了最大累计损失 \(L\) 以及盈余过程在创新下纪录时的盈余差额 \(L_1,L_2,L_3\) 之间的关系：

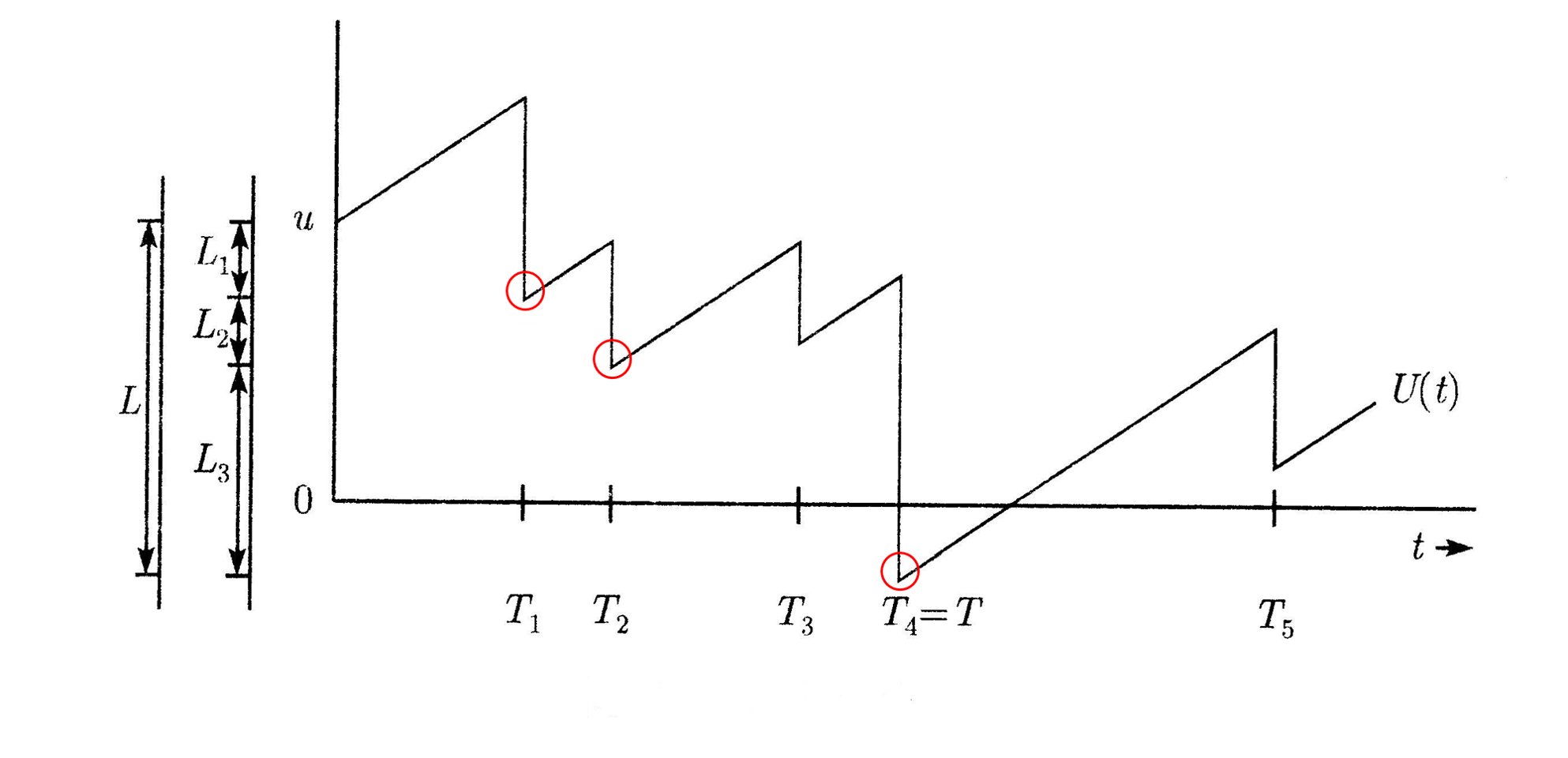
由于泊松过程是无记忆的，因此对 \(M\) 和 \(L\) 具有如下的性质：

• 任何一个下纪录都是最后一次下纪录的概率是相同的，因此 \(M\) 服从一个几何分布。
• \(M\) 的参数为前一个创新下纪录是最后一个最后一个的概率，等于盈余过程从初始资本金 \(0\) 出发而没有发生破产的概率，故该参数等于 \(1-\psi(0)\) 。
• 由于 \(\{L_j,j=1,2,\cdots\}\) 是独立同分布的，所以 \(L\) 服从一个复合几何分布，参数为 \(1-\psi(0)\) 。

二、破产时刻资本金的分布

接下来我们介绍一个关于破产时刻资本金的分布的定理。

定理：如果初始资本金 \(u=0\) ，则对所有 \(y>0\) ，都有

\[{\rm Pr}\left[U(T)\in(-y-{\rm d}y,-y),\ T<\infty\right]=\frac{\lambda}{c}[1-P(y)]{\rm d}y. \]

其中 \(P(y)\) 是索赔额 \(X\) 的分布函数。

证明：记

\[G(u,y)\xlongequal{def}{\rm Pr}\left[U(T)\in(-\infty,-y),T<\infty\mid U(0)=u\right], \]

显然有

\[\lim_{u\to\infty}G(u,y)=\lim_{u\to\infty}{\rm Pr}\left[U(T)\in(-\infty,-y),T<\infty\mid U(0)=u\right]=0. \]

在复合泊松过程下，在时间区间 \((0,{\rm d}t)\) 只可能发生一次理赔或没有发生理赔。

(1) 若没有发生理赔，该概率为 \(1-\lambda{\rm d}t\) ，则 \((0,{\rm d}t)\) 时间内一定不会破产；

(2) 若发生一个理赔，该概率为 \(\lambda{\rm d}t\) ，发生破产的情况是：

• 如果该理赔额小于 \(u+c{\rm d}t\) ，即 \(X<u+c{\rm d}t\) ，则 \((0,{\rm d}t)\) 时间内一定不会破产，过程将以初始资本金 \(u+c{\rm d}t-X\) 继续下去；
• 如果该理赔额大于 \(u+c{\rm d}t\) ，即 \(X>u+c{\rm d}t\) ，则破产会发生，即 \(T<\infty\) 。根据破产时理赔额的大小又分为两种情况：
  • 若 \(X\leq u+c{\rm d}t+y\) ，则破产时刻 \(U(T)>-y\) 。
  • 若 \(X>u+c{\rm d}t+y\) ，则破产时刻 \(U(T)<-y\) ，即亏损会大于 \(y\) 。

根据以上讨论，则有

\[\begin{aligned} G(u,y)&=(1-\lambda{\rm d}t)G(u+c{\rm d}t,y) \\ \\ &\quad\;+\;\lambda{\rm d}t\left[\int_0^{u+c{\rm d}t}G(u+c{\rm d}t-x,y){\rm d}P(x)+\int_{u+c{\rm d}t+y}^\infty1{\rm d}P(x)\right]. \end{aligned} \]

整理之后有

\[\begin{aligned} &\frac{G(u+c{\rm d}t,y)-G(u,y)}{c{\rm d}t} \\ \\ =\;&\frac{\lambda}{c}G(u+c{\rm d}t,y)-\frac{\lambda}{c}\left[\int_0^{u+c{\rm d}t}G(u+c{\rm d}t-x,y){\rm d}P(x)+\int_{u+c{\rm d}t+y}^\infty1{\rm d}P(x)\right]. \end{aligned} \]

设 \(G''\) 为函数 \(G\) 关于 \(u\) 偏导数，并令 \({\rm d}t\to0\) ，我们得到

\[G'(u,y)=\frac{\lambda}{c}\left[G(u,y)-\int_0^{u}G(u-x,y){\rm d}P(x)-\int_{u+y}^\infty1{\rm d}P(x)\right]. \]

再对上式求 \(u\in[0,z]\) 上的积分可得

\[\begin{aligned} &G(z,y)-G(0,y) \\ \\ =\;&\frac{\lambda}{c}\left[\int_0^zG(u,y){\rm d}u-\int_0^z\int_0^{u}G(u-x,y){\rm d}P(x){\rm d}u-\int_0^z\int_{u+y}^\infty1{\rm d}P(x){\rm d}u\right] \\ \\ =\;&\frac{\lambda}{c}\left[\int_0^zG(u,y){\rm d}u-\Delta_1-\Delta_2\right]. \end{aligned} \]

对于第一个二重积分，交换积分次序，使用变量代换 \(v=u-x\) ，再交换积分次序，于是有

\[\begin{aligned} \Delta_1&=\int_0^z\int_0^{u}G(u-x,y){\rm d}P(x){\rm d}u \\ \\ &=\int_0^z\int_x^zG(u-x,y){\rm d}u{\rm d}P(x) \\ \\ &=\int_0^z\int_0^{z-x}G(v,y){\rm d}v{\rm d}P(x) \\ \\ &=\int_0^z\int_0^{z-v}G(v,y){\rm d}P(x){\rm d}v \\ \\ &=\int_0^zG(v,y)P(z-v){\rm d}v. \end{aligned} \]

对于第二个二重积分，使用变量代换 \(v=u+y\) 可得

\[\Delta_2=\int_0^z\int_{u+y}^\infty{\rm d}P(x){\rm d}u=\int_y^{z+y}\left[1-P(v)\right]{\rm d}v. \]

从而有

\[G(z,y)-G(0,y)=\frac{\lambda}{c}\left[\int_0^zG(u,y)\left[1-P(z-u)\right]{\rm d}u-\int_y^{z+y}\left[1-P(v)\right]{\rm d}v\right]. \]

取 \(z\to\infty\) ，上式两边的第一项消失，则有

\[G(0,y)=\frac\lambda c\int_y^\infty\left[1-P(v)\right]{\rm d}v. \]

推论1：初始值为 \(0\) 的破产概率只依赖于相对安全附加系数 \(\theta\) 。

由破产时刻资本金的分布

\[{\rm Pr}\left[U(T)\in(-y-{\rm d}y,-y),\ T<\infty\right]=\frac{\lambda}{c}[1-P(y)]{\rm d}y. \]

对 \(y\in(0,\infty)\) 积分可得 \({\rm Pr}\left[T<\infty\right]\) 的值，即

\[\psi(0)=\frac{\lambda}{c}\int_0^\infty\left[1-P(v)\right]{\rm d}v=\frac{\lambda}{c}\mu_1=\frac{1}{1+\theta}. \]

推论2：设至少有一个创新下纪录，则 \(L_1\) 与起始于 \(u=0\) 的过程，如果破产发生，则在破产时刻的数值具有相同的分布函数。

随机变量 \(\{L_j,j=1,2,\cdots\}\) 表示第 \(j\) 个创新下纪录小于第 \(j-1\) 个创新下纪录的量，故 \(L_j\) 独立同分布且具有如下形式：

\[{\rm Pr}\left[L_1>y\mid T<\infty\right]=\frac{{\rm Pr}\left[L_1>y,T<\infty\right]}{{\rm Pr}(T<\infty)}, \\ \\ f_{L_1}(y)=\frac{1-P(y)}{(1+\theta)\mu_1}\frac{1}{\psi(0)}=\frac{1-P(y)}{\mu_1},\quad y>0. \]

推论3：记 \(H(x)\) 为 \(L_1\) 的分布函数，\(p\) 为 \(M\) 的参数。因为 \(L\) 服从复合几何分布，所以风险过程的未破产概率可以由 Beekman 卷积公式给出：

\[1-\psi(u)=\sum_{m=0}^\infty p(1-p)^mH^{m*}(u), \]

其中

\[p=\frac{\theta}{1+\theta},\quad H(x)=1-\frac1{\mu_1}\int_x^\infty\left[1-P(v)\right]{\rm d}v. \]

注意：这个结论与第一节采用概率论的方法得出的破产概率的表达式是一致的。

推论4：由 \(\psi(u)=1-F_L(u)\) 最大累积损失 \(L\) 的矩母函数也是未破产概率 \(1-\psi(u)\) 的矩母函数，该矩母函数由下式给出：

\[m_L(r)=\frac{\theta}{1+\theta}+\frac{1}{1+\theta}\frac{\theta\left(m_X(r)-1\right)}{1+(1+\theta)\mu_1r-m_X(r)}. \]

由于 \(L=L_1+L_2+\cdots+L_M\) 且 \(M\) 服从参数为 \(p\) 的几何分布，其中 \(p=\theta/(1+\theta)\) ，则有

\[m_L(r)=m_M\left(\ln m_{L_1}(r)\right)=\frac{p}{1-(1-p)m_{L_1}(r)}. \]

由 \(L_1\) 的密度函数公式，可得 \(L_1\) 的矩母函数为

\[\begin{aligned} m_{L_1}(r)&=\frac{1}{(1+\theta)\mu_1}\int_0^\infty e^{ry}P(y){\rm d}y \\ \\ &=\frac{1}{(1+\theta)\mu_1}\left[\frac1r\left[e^{ry}-1\right]\left[1-P(y)\right]\bigg|_0^\infty+\int_0^\infty\frac1r\left[e^{ry}-1\right]\left[1-P(y)\right]{\rm d}y \right] \\ \\ &=\frac{1}{(1+\theta)\mu_1r}\left[m_X(r)-1\right]. \end{aligned} \]

所以 \(L\) 的矩母函数为

\[\begin{aligned} m_L(r)&=\frac{p}{1-(1-p)m_{L_1}(r)} \\ \\ &=\frac{\theta}{1+\theta}\frac{1}{1-\frac{1}{1+\theta}\frac{1}{(1+\theta)\mu_1r}\left[m_X(r)-1\right]} \\ \\ &=\frac{\theta}{1+\theta}+\frac{1}{1+\theta}\frac{\theta\left(m_X(r)-1\right)}{1+(1+\theta)\mu_1r-m_X(r)}. \end{aligned} \]

三、破产概率的解析表达式

由于 \(L\) 的分布函数为 \(1-\psi(u)\) ，故 \(L\) 的矩母函数可以写为

\[m_L(r)=\int_0^\infty e^{ru}{\rm d}\left[1-\psi(u)\right]=1-\psi(0)+\int_0^\infty e^{ru}\left(-\psi^\prime(u)\right){\rm d}u. \]

由上面的讨论知，\(L\) 的矩母函数为

\[m_L(r)=\frac{\theta}{1+\theta}+\frac{1}{1+\theta}\frac{\theta\left(m_X(r)-1\right)}{1+(1+\theta)\mu_1r-m_X(r)}. \]

联立有

\[\int_0^\infty e^{ru}\left(-\psi^\prime(u)\right){\rm d}u=\frac{1}{1+\theta}\frac{\theta\left(m_X(r)-1\right)}{1+(1+\theta)\mu_1r-m_X(r)}. \]

由此可以由 Laplace 逆变换解得 \(\psi(u)\) 的解析表达式。

例如：假设 \(\theta=0.4\) ，索赔额 \(X\) 的密度函数为

\[p(x)=\frac12\times 3e^{-3x}+\frac12\times 7e^{-7x},\quad x>0. \]

计算可得

\[\begin{aligned} &m_X(r)=\frac{1}{2}\times\frac{3}{3-r}+\frac12\times\frac{7}{7-r}, \\ \\ &\mu_1=\frac{1}{2}\times\frac13+\frac12\times\frac17=\frac{5}{21}. \end{aligned} \]

代入后有

\[\frac{1}{1+\theta}\frac{\theta\left(m_X(r)-1\right)}{1+(1+\theta)\mu_1r-m_X(r)}=\frac{6(5-r)}{7(6-7r+r^2)}=\frac{24}{35}\frac{1}{1-r}+\frac1{35}\frac{6}{6-r}. \]

根据上面的讨论可知

\[\int_0^\infty e^{ru}\left(-\psi^\prime(u)\right){\rm d}u=\frac{24}{35}\frac{1}{1-r}+\frac1{35}\frac{6}{6-r}, \\ \\ \Downarrow \quad r=-t \\ \\ \int_0^\infty e^{-tu}\left(-\psi^\prime(u)\right){\rm d}u=\frac{24}{35}\frac{1}{1+t}+\frac1{35}\frac{6}{6+t}. \]

由拉普拉斯逆变换可知

\[-\psi^\prime(u)=\frac{24}{35}e^{-u}+\frac6{35}e^{-6u}. \]

由此得出破产概率为

\[\psi(u)=\frac{24}{35}e^{-u}+\frac1{35}e^{-6u}. \]