现代精算风险理论08：破产概率(1)

目录

• 第八讲 破产概率(1)
  • 第一节 风险过程和破产概率
    • 一、经典破产理论简介
    • 二、经典破产过程
  • 第二节 经典破产概率研究方法
    • 一、概率论方法
    • 二、微分方程方法
  • 第三节 调节系数与破产概率的指数上界
    • 一、调节系数
    • 二、破产概率的指数上界

第八讲 破产概率(1)

第一节 风险过程和破产概率

一、经典破产理论简介

在保险精算数学的范畴内，破产理论是风险理论的核心内容。本节我们将基于长期的视角，再次关注聚合风险模型，考虑保险人的资本金 \(U(t)\) 随时间的积累问题。

这个问题可以用随机过程 \(\{U(t),t\geq0\}\) 来刻画，该随机过程随着保费收入连续增加，而在理赔发生时阶梯下降，当资本金变为负值时，即为破产发生了。

假设年保费率和理赔过程保持不变，以 \(\psi(u)\) 表示初始资本金为 \(u=U(0)\) 时的破产概率，这个概率是一个特殊的风险度量，用来描述保险公司保费和理赔过程组合的稳定性。

破产概率高，意味着保险公司经营不稳定，保险公司应该考虑采取再保险或者提高保费等措施，或者设法吸引更多的营运资金。

注意：保险人通常的组织形式是公司，所以我们不严格区分保险人和保险公司的说法。

二、经典破产过程

由于经典破产培训假设独立同分布的索赔的到达服从泊松过程，所以首先回忆一下泊松过程的定义。

泊松过程：随机过程 \(\{N(t),t\geq0\}\) 称为是一个强度为 \(\lambda\) 的泊松过程，如果对 \(\forall h>0\) ，满足

1. \(N(t+h)-N(t)\sim P(\lambda h)\) ；

2. 独立增量性：对 \(\forall \{(t_i,t_i+h_i),\ i=1,2,\cdots\}\) 两两不交，有 \(N(t_i+h_i)-N(t_i)\) 相互独立。

3. 平稳增量性：对 \(\forall t>0\) ，有 \(N(t+h)-N(t)\) 具有相同的分布。

下面建立经典破产模型，首先给出盈余过程或风险过程的定义，以及经典破产模型需要满足的假设。

风险过程 / 盈余过程：定义盈余过程或者风险过程的形式为

\[U(t)=u+ct-S(t),\quad t\geq0, \]

其中

\[\begin{aligned} U(t)&= \text{保险人在时刻 } t \text{ 的资本金}; \\ \\ u&=U(0)=\text{初始资本金}; \\ \\ c&=\text{单位时间的保费收入（常数）}; \\ \\ S(t)&=X_1+X_2+\cdots+X_{N(t)}. \end{aligned} \]

并且

\[\begin{aligned} N(t)&=\text{到时刻 }t\text{ 为止的理赔次数};\\ \\ X_i&=\text{第 }i\text{ 个理赔额}. \end{aligned} \]

假设 1：假设 \(N(t)\) 是参数为 \(\lambda\) 的泊松过程，其概率分布为

\[{\rm Pr}(N(t)=k)=e^{-\lambda t}\frac{(\lambda t)^k}{k!},\quad k=1,2,\cdots. \]

由假设 1 可知，如果假设索赔发生的时间为 \(0<T_1<T_2<\cdots\) ，则 \(T_1,T_2,\cdots\) 是随机变量，且索赔发生的时间间隔为

\[Y_1=T_1,\quad Y_k=T_k-T_{k-1},\quad k=2,3,\cdots, \]

则 \(Y_k\) 为独立同分布的随机变量，服从参数为 \(\lambda\) 的指数分布。

假设 2：假设所有的索赔额 \(X_i\) 相互独立同分布，与 \(X\) 具有相同的分布函数 \(F(x)={\rm Pr}(X\leq x)\) ，并且与 \(N(t)\) 相互独立，对某些 \(r>0\) ，矩母函数存在，即

\[m_X(r)=\mathbb{E}\left[e^{rX}\right]<\infty. \]

由假设 2 可知，记 \(\mu_j=\mathbb{E}\left[X^j\right],\ j=1,2,\cdots\) ，则对于盈余过程，有

\[\mathbb{E}\left[U(t)\right]=u+ct-\lambda\mu_1t. \]

假设 3：假设安全负荷系数 \(\theta>0\) 。安全负荷系数由下面的公式给出：

\[\theta=\frac{c}{\lambda\mu_1}-1>0. \]

如果将破产视为一个事件，则破产可以被定义为：在盈余过程中的某个时刻，发生的总理赔额大于初始资本金加上所收取的保费的状态，即资本金盈余小于 \(0\) 的状态。

例如：下图描述了风险过程一个典型的实现形式，随机变量 \(T_1,T_2,\cdots\) 表示每个理赔发生的时刻：

• 在没有理赔发生的时候该过程图形的斜率是 \(c\) ；
• 在第 \(j\) 个理赔发生的时刻 \(T_j\) ，资本金就减少 \(X_j\) ，这里 \(X_j\) 是第 \(j\) 个理赔额。

在时刻 \(T_4\) ，因为总理赔额 \(X_1+X_2+X_3+X_4\) 大于初始资本金加上所收取的保费 \(u+cT_4\) ，所以资本金盈余 \(U(T_4)<0\) ，过程的这种状态称为破产。

由盈余过程或者风险过程的定义，我们将定义中的 \(S(t)\) 称为总索赔过程。

总索赔过程：\(S(t)\) 称为总索赔过程：

\[S(t)=\left\{\begin{array}{ll} \displaystyle\sum_{i=1}^{N(t)}X_i, & N(t)>0, \\ \\ 0, & N(t)=0. \end{array}\right. \]

总索赔过程的分布：

\[G_t(x)={\rm Pr}(S(t)\leq x)=\sum_{n=0}^\infty e^{-\lambda t}\frac{(\lambda t)^n}{n!}F^{n*}(x),\quad x\geq 0,\quad t\geq0. \]

其中

\[F^{n*}(x)={\rm Pr}\left(\sum_{i=1}^nX_i\leq x\right). \]

并且

\[F^{0*}=\left\{\begin{array}{ll} 1 , & x\geq0, \\ \\ 0 , & x<0. \end{array}\right. \]

总索赔过程的均值函数为

\[\mathbb{E}[S(t)]=\mathbb{E}[N(t)]\mathbb{E}(X)=\lambda\mu_1 t. \]

若采用均值保费计算原理，则有

\[ct=(1+\theta)\lambda\mu_1 t. \]

由此得出安全负荷系数

\[\theta=\frac{c}{\lambda\mu_1}-1>0. \]

由盈余过程或者风险过程的定义，可以导出破产时间和破产概率的定义。

破产时间：分为有限破产时间和无限破产时间两类。

• 有限破产时间：

  \[T(t_0)=\inf\{t:0\leq t\leq t_0,\ u(t)<0|u(0)=u\},\quad 0<t_0<\infty. \]

• 无限破产时间：

  \[T=\inf\{t:0\leq t\leq\infty,\ u(t)<0|U(0)=u\}. \]

• 如果对 \(\forall t>0\) ，都有 \(U(t)\geq0\) ，则定义破产时间为 \(\infty\) 。

破产概率：分为有限时间的破产概率和无限时间的破产概率两类。

• 有限时间的破产概率：

  \[\psi(u,t_0)={\rm Pr}\left[U(t)<0,\exists 0\leq t\leq t_0|u(0)=u\right], \quad 0<t_0<\infty. \]

• 无限时间的破产概率 / 最终破产概率：

  \[\psi(u)=\psi(u,\infty)={\rm Pr}(T<\infty|U(0)=u). \]

注意：这里的无限破产时间 \(T\) 是一个特殊的随机变量，称为广义实值随机变量。这是因为

\[{\rm Pr}(T=\infty)=p>0,\quad {\rm Pr}(T<\infty)=1-p. \]

而对于一般的实值随机变量，应该有 \({\rm Pr}(T<\infty)=1\) 。

第二节 经典破产概率研究方法

一、概率论方法

引理：平衡分布

设非负随机变量 \(X\) 具有分布函数 \(F(x)\) ，其均值为 \(\mathbb{E}(X)=\mu_1\) ，定义其平衡分布为

\[F_I(x)=\frac1{\mu_1}\int_0^{x}\overline{F}(y){\rm d}y, \quad x\geq0. \]

容易验证 \(F_I(x)\) 是一个分布函数，设其对应的随机变量 \(X_I\) 称为随机变量 \(X\) 的伪随机变量。

平衡分布经常在风险理论中出现，可以用来刻画平均剩余寿命的特征。

由风险过程可知，破产仅可能发生在有索赔的时刻 \(T_i,\ i=1,2,\cdots\) ，故

\[\begin{aligned} \psi(u)&={\rm Pr}\left(u+ct-S(t)<0,\ \exists t\geq0\right) \\ \\ &={\rm Pr}\left(u+cT_n-S(T_n)<0,\ \exists n\geq1\right) \\ \\ &={\rm Pr}\left(u+\sum_{k=1}^n(cY_k-X_k)<0,\ \exists n\geq1\right) \\ \\ &={\rm Pr}\left(\sup_{n\geq1}\sum_{k=1}^n(X_k-cY_k)>u\right) \end{aligned} \]

令 \(Z_k=X_k-cY_k,\ k=1,2,\cdots,n\) ，记

\[R_0=0,\quad R_n=\sum_{k=1}^nZ_k ,\quad n\geq1. \]

则随机过程 \(\{R_n,n\geq1\}\) 是一个随机游动过程。

如果将破产概率 \(\psi(u)\) 的反面称为生存概率，即 \(1-\psi(u)\) ，则有

\[1-\psi(u)=\mathrm{Pr}\left(\sup_{n\geq1}R_n\leq u\right). \]

根据随机游动中的 Spitzer 恒等式，我们可以得出最终破产概率的结果

\[1-\psi(u)=\frac{\theta}{1+\theta}\sum_{n=0}^\infty(1+\theta)^{-n}F_I^{n*}(u), \]

或可以写为

\[\psi(u)=\frac{\theta}{1+\theta}\sum_{n=0}^\infty(1+\theta)^{-n}\overline{F}_I^{n*}(u), \]

这里 \(F_I^{n*}(u)\) 指的是平衡分布 \(F_I(x)\) 的 \(n\) 重卷积，即如果 \(X_i\) 的伪随机变量为 \({X_I}_i\) ，则

\[F_I^{n*}(u)={\rm Pr}\left(\sum_{i=1}^n{X_I}_i\leq u\right). \]

但是，这样的破产概率的计算是非常复杂的，只有某些具体的分布是可以精确计算的。

例如：假设风险 \(X\) 服从均值为 \(\mu\) 的指数分布，则破产概率为

\[\psi(u)=\frac{1}{1+\theta}\exp\left\{-\frac{\theta}{\mu(1+\theta)}u\right\},\quad u\geq0. \]

证明：容易验证，指数分布的平衡分布 \(F_I(x)=F(x)\) 。

如果 \(X_i\) 相互独立，且服从均值为 \(\mu\) 的指数分布，则有

\[\sum_{i=1}^nX_i\sim\Gamma\left(n,\frac1\mu\right). \]

因此有

\[\overline{F}^{n*}_I(u)={\rm Pr}\left(\Gamma\left(n,\frac1\mu\right)>u\right)=\int_u^\infty\frac{1}{\mu^n\Gamma(n)}x^{n-1}\exp\left\{-\frac x\mu\right\}{\rm d}x. \]

由此可得

\[\begin{aligned} \psi(u)&=\frac{\theta}{1+\theta}\sum_{n=1}^\infty(1+\theta)^{-n}\int_u^\infty\frac{1}{\mu^n\Gamma(n)}x^{n-1}\exp\left\{-\frac x\mu\right\}{\rm d}x \\ \\ &=\frac{\theta}{1+\theta}\int_u^\infty\sum_{n=1}^\infty\frac{1}{\left(\mu(1+\theta)\right)^n\Gamma(n)}x^{n-1}\exp\left\{-\frac x\mu\right\}{\rm d}x \\ \\ &=\frac{\theta}{1+\theta}\int_u^\infty\frac{1}{\mu(1+\theta)}\sum_{n=0}^\infty\frac{1}{\left(\mu(1+\theta)\right)^nn!}x^{n}\exp\left\{-\frac x\mu\right\}{\rm d}x \\ \\ &=\frac{\theta}{1+\theta}\int_u^\infty\frac{1}{\mu(1+\theta)}\exp\left\{-\frac{\theta x}{\mu(1+\theta)}\right\}{\rm d}x \\ \\ &=\frac{1}{1+\theta}\exp\left\{-\frac{\theta}{\mu(1+\theta)}u\right\}. \end{aligned} \]

从这个例子可以看出：

• 如果 \(\theta=0\) ，则 \(\psi(u)=1\) ，即以概率 \(1\) 破产。
• 如果初始盈余 \(u=0\) ，则 \(\psi(0)=\dfrac{1}{1+\theta}\) 。

二、微分方程方法

记 \(\delta(u)=1-\psi(u)\) 称为生存函数，则有

\[\begin{aligned} \delta(u)&={\rm Pr}\left(S(t)-ct\leq u , \ \forall t\geq0\right) \\ \\ &={\rm Pr}\left(\sum_{k=1}^n(X_k-cY_k)\leq u , \ \forall n\geq1\right) \\ \\ &={\rm Pr}\left(\sum_{k=2}^n(X_k-cY_k)\leq u+cY_1-X_1 , \ \forall n\geq2,\ X_1-cY_1\leq u\right) \\ \\ &={\rm Pr}\left(S'(t)-ct\leq u+cY_1-X_1 , \ \forall t\geq0,\ X_1-cY_1\leq u\right), \end{aligned} \]

其中 \(S'(t)\) 与 \((X_1,Y_1)\) 相互独立，且与 \(S(t)\) 具有相同的分布。所以

\[\begin{aligned} \delta(u)&=\int_0^\infty\int_0^{u+cs}{\rm Pr}\left(S'(t)-ct\leq u+cs-x,\forall t>0\right){\rm d}F(x)\lambda e^{-\lambda s}{\rm d}s \\ \\ &=\int_0^\infty\int_0^{u+cs}\delta(u+cs-x){\rm d}F(x)\lambda e^{-\lambda s}{\rm d}s \\ \\ &=\frac{\lambda}{c}e^{u\lambda/c} \int_u^\infty e^{-\lambda z/c}\left[\int_0^z\delta(z-x){\rm d}F(x) \right]{\rm d}z. \end{aligned} \]

其中，最后一个等式由积分变换 \(u+cs=z\) 得出。

对方程的两边求导后得

\[\delta'(u)=\frac\lambda c\delta(u)-\frac\lambda c\int_0^u\delta(u-x){\rm d}F(x). \]

用 \(1-\psi(u)\) 替代 \(\delta(u)\) 可得破产概率的微分方程公式

\[c\psi'(u)+\lambda\left\{\int_0^u\psi(u-x)f(x){\rm d}x+1-F(u)-\psi(u)\right\}=0. \]

解微分方程可得破产概率。然而，想要得到一个微分方程的唯一解，只有微分方程的表达式是不够的，还需要一个初值或边界值，因此我们需要考虑 \(\delta(0)\) 的情况。

考虑初始盈余为 \(0\) 时的破产概率，对破产概率的微分方程两边求积分

\[\delta'(u)=\frac\lambda c\delta(u)-\frac\lambda c\int_0^u\delta(u-x){\rm d}F(x). \\ \\ \begin{aligned} \delta(u)-\delta(0)&=\frac{\lambda}{c}\int_0^u\delta(z){\rm d}z-\frac\lambda c\int_0^u\int_0^z\delta(z-x){\rm d}F(x) {\rm d}z \\ \\ (*)&=\frac{\lambda}{c}\int_0^u\delta(u-x){\rm d}x-\frac\lambda c\int_0^u\int_0^z\delta(z-x){\rm d}F(x) {\rm d}z \\ \\ &=\frac\lambda c\int_0^u\delta(u-x)(1-F(x)){\rm d}x. \end{aligned} \]

第二个等号 \((*)\) 的前一部分由 \(z=u-x\) 变换得到。令 \(u\to\infty\) 得

\[c(1-\delta(0))=\lambda\int_0^\infty(1-F(x)){\rm d}x=\lambda\mu_1, \]

所以解得

\[\delta(0)=1-\frac{\lambda\mu_1}{c}=\frac{1}{1+\theta}. \]

其中 \(\mu_1=\mathbb{E}(X)\) ，\(\theta\) 为安全负荷系数。

在实际应用中，破产概率微分方程也并不容易求解，往往要通过微分方程数值解的方式进行近似计算，只有某些具体的分布是可以精确计算的。

例如：假设风险 \(X\) 服从均值为 \(\mu\) 的指数分布，则破产概率微分方程改写为

\[c\delta'(u)=\lambda\left[\delta(u)-e^{-\alpha u}\int_0^u\delta(y)\alpha e^{\alpha y}{\rm d}y\right],\quad \alpha=\frac1\mu. \]

进一步对其两边求导可得

\[d\delta''(u)=\lambda\delta'(u)-\alpha c\delta'(u), \]

上述微分方程的通解为

\[\delta(u)=A+Be^{-(\alpha-\lambda/c)u}. \]

由于当 \(u\to\infty\) 时，\(\delta(u)\to1\) ，所以 \(A=1\) ；又由于 \(\delta(0)=1-\dfrac{\lambda\mu}{c}\) ，所以 \(B=-\dfrac{\lambda\mu}{c}\) 。

因此，索赔 \(X\) 为指数分布情形下的生存概率为

\[\delta(u)=1-\frac{\lambda\mu}{c}e^{-(\alpha-\lambda/c)u}. \]

所以，破产概率为

\[\psi(u)=\frac{\lambda\mu}{c}e^{-(\alpha-\lambda/c)u}. \]

由 \(c=(1+\theta)\mu\lambda\) ，代入则有

\[\psi(u)=\frac1{1+\theta}\exp\left\{-\left(\frac 1\mu-\frac{1}{(1+\theta)\mu}\right)u\right\}=\frac1{1+\theta}\exp\left\{-\frac{\theta}{(1+\theta)\mu}u\right\}. \]

第三节 调节系数与破产概率的指数上界

一、调节系数

调节系数：设理赔 \(X\geq0\) ，满足 \(\mathbb{E}(X)=\mu_1>0\) ，称关于 \(r\) 的方程

\[1+(1+\theta)\mu_1r=m_X(r) \]

为调节系数方程，调节系数方程有一个正数解，记为 \(R\) ，称为 \(X\) 的调节系数。调节系数是关于风险过程的风险度量，注意到，调节系数 \(R\) 不依赖于泊松参数 \(\lambda\) 。

调节系数的存在性由以下性质保证，如图所示：

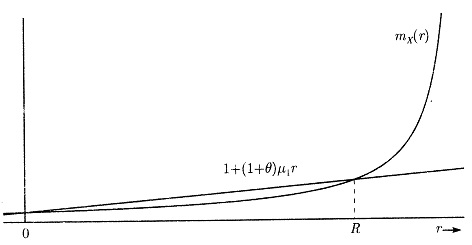
1. 矩母函数 \(m_X(t)\) 是严格凸的，因为

\[ m''_X(t)=\mathbb{E}\left[X^2e^{tX}\right]>0. \]

2. 矩母函数的一阶导数满足

\[ m_X'(0)=\mathbb{E}(X)=\mu_1<(1+\theta)\mu_1. \]

3. 对于非负随机变量，几乎无一例外的有 \(m_X(t)\) 连续趋近于 \(\infty\) 。

由调节系数的存在性证明，可以进一步得出：

• 当 \(\theta\downarrow0\) 时，调节系数 \(R\) 的极限为 \(0\) ；

• 当 \(\theta\uparrow\infty\) 时，调节系数 \(R\) 趋近于 \(m_X(t)\) 的渐近线或 \(\infty\) 。

定理：调节系数满足以下三个等价方程

\[\begin{array}{ll} (1)\qquad &\qquad \lambda+cR=\lambda m_X(R), \\ \\ (2)\qquad &\qquad \displaystyle\int_0^\infty\left[e^{Rx}-(1+\theta)\right][1-F(x)]{\rm d}x=0, \\ \\ (3)\qquad &\qquad e^{Rc}=\mathbb{E}\left[e^{RS}\right] , \end{array} \]

其中，\(S\) 表示在长度为 \(1\) 的时间区间上的理赔总额，即

\[S=\sum_{i=0}^{N(1)}X_i. \]

由此可以得出以下几条性质：

(1) 复合泊松分布 \(S\) 的矩母函数为

\[\mathbb{E}\left[e^{RS}\right]=\exp\left\{\lambda(m_X(R)-1)\right\}. \]

(2) 从方程 \(e^{Rc}=\mathbb{E}\left[e^{RS}\right]\) 可以看出， \(c\) 可以看成风险厌恶系数为 \(R\) 的指数保费

\[c=\frac1R\ln m_S(R). \]

(3) 方程 \(e^{Rc}=\mathbb{E}\left[e^{RS}\right]\) 可以类似推广到对任意长度 \(t\) 的时间区间上的理赔总额，即

\[e^{Rct}=\mathbb{E}\left[e^{RS(t)}\right],\quad S(t)=\sum_{i=1}^{N(t)}X_i. \]

例如（指数分布下的调节系数）：设 \(X\) 服从一个参数为 \(\beta=1/\mu_1\) 的指数分布，则对应的调节系数是如下方程的解：

\[1+(1+\theta)\mu_1r=m_X(r)=\frac{\beta}{\beta-r}, \]

该方程有一个平凡解 \(r=0\) 和另一个正数解，即调节系数

\[R=\frac{\theta\beta}{1+\theta}. \]

在损失分布是指数分布的情形下，调节系数有一个清晰的表达式。

例如（混合指数分布下的调节系数）：设 \(Y\) 是一个非负随机变量，具有分布函数

\[G(x)=1-pe^{-\alpha x}-(1-p)e^{-\beta x}. \]

其中 \(0<\alpha<\beta\) ，并且 \(0<p\leq\beta(\beta-\alpha)^{-1}\) 。注意到 \(Y\) 的均值为

\[\mu_1=\mathbb{E}(Y)=\frac{p}{\alpha}+\frac{1-p}{\beta}. \]

所以有

\[c>\frac{\lambda p}{\alpha}+\frac{\lambda(1-p)}{\beta},\quad \left(\theta=\frac{c}{\lambda\mu_1}-1>0\right) \]

对于 \(r<\alpha\) ，有

\[m_Y(r)=\frac{\alpha p}{\alpha-r}+\frac{\beta(1-p)}{\beta-r}. \]

所以调节系数方程可以写为

\[\lambda\left(m_Y(r)-1\right)-cr=\lambda\left(\frac{r p}{\alpha-r}+\frac{r(1-p)}{\beta-r}\right)-cr=0. \]

如果 \(r\neq0\) ，则有

\[\lambda p(\beta-r)+\lambda(1-p)(\alpha-r)=c(\alpha-r)(\beta-r). \]

解得

\[r=\frac12\left(\alpha+\beta-\frac{\lambda}{c}\pm\sqrt{\left(\alpha+\beta-\frac{\lambda}{c}\right)^2+\frac{4p\lambda}{c}(\beta-\alpha)}\right). \]

由于 \(Y\) 矩母函数 \(m_Y(r)\) 在 \(r\geq\alpha\) 时不存在，所以调节系数为

\[R=\frac12\left(\alpha+\beta-\frac{\lambda}{c}-\sqrt{\left(\alpha+\beta-\frac{\lambda}{c}\right)^2+\frac{4p\lambda}{c}(\beta-\alpha)}\right). \]

二、破产概率的指数上界

破产概率的指数上界，也称为破产概率的 Lundberg 指数上界，该定理具有一个简洁而优美的证明，使用的方法仅仅是数学归纳法。该定理有助于后面推导具有指数理赔额的泊松破产过程的破产概率。

定理：假设存在常数调节系数 \(R>0\) ，则有

\[\psi(u)\leq e^{-Ru}. \tag{a} \]

进一步，假设

\[\int_0^\infty xe^{Rx}\overline{F}(x){\rm d}x<\infty, \]

则有

\[\lim_{u\to\infty} e^{Ru}\psi(u)=C<\infty. \tag{b} \]

其中

\[C=\left[\frac{R}{\theta\mu_1}\int_0^\infty xe^{Rx}\overline{F}(x){\rm d}x\right]^{-1}. \]

这里我们只给出 \((a)\) 的证明过程。

记 \(\psi_k(u)\) 为破产发生在第 \(k\) 个理赔来到的时刻或之前的概率，其中 \(-\infty<u<\infty,\ k=0,1,\cdots\) 。

对所有的 \(u\) ，当 \(k\to\infty\) 时，有 \(\psi_k(u)\) 的极限等于 \(\psi(u)\) 。

故只需证 \(\psi_k(u)\leq e^{-Ru}\) 对每一个 \(k=0,1,\cdots\) 成立即可。

用数学归纳法。

(1) 当 \(k=0\) 时，由于当 \(u<0\) 时，有 \(\psi_0(u)=1\) ；当 \(u\geq0\) 时，有 \(\psi_0(u)=0\) 。故不等式成立。

(2) 当 \(k=1\) 时，计算可得

\[\begin{aligned} \psi_1(u)&={\rm Pr}\left(u+cT_1-X_1<0\right) \\ \\ &=\int\int_{u+ct-x<0}1{\rm d}F(x)\lambda e^{-\lambda t}{\rm d}t \\ \\ &\leq \int\int_{u+ct-x<0} \exp\left\{-R(u+ct-x)\right\}{\rm d}F(x)\lambda e^{-\lambda t}{\rm d}t \\ \\ &\leq \int_0^\infty\int_0^\infty\exp\left\{-R(u+ct-x)\right\}{\rm d}F(x)\lambda e^{-\lambda t}{\rm d}t \\ \\ &=e^{-Ru}. \end{aligned} \]

(3) 假设对 \(m\leq k-1\) 都有 \(\psi_{m}(u)\leq e^{-Ru}\) 成立。

如果破产发生在 \(k\) 时刻之前，则由归纳假设可得 \(\psi_{m}(u)\leq e^{-Ru},\ m\leq k-1\) 。

如果破产发生在 \(k\) 时刻，则有

\[\begin{aligned} \psi_k(u)&={\rm Pr}\left(u+\sum_{i=1}^k(cT_i-X_i)<0\right) \\ \\ &={\rm Pr}\left(u+\sum_{i=1}^{k-1}(cT_i-X_i)<X_k-cT_k\right) \\ \\ &=\int_0^\infty\int_0^\infty{\rm Pr}\left(u+\sum_{i=1}^{k-1}(cT_i-X_i)<x-ct\right){\rm d}F(x)\lambda e^{-\lambda t}{\rm d}t \\ \\ &=\int_0^\infty\int_0^\infty{\rm Pr}\left((u-x+ct)+\sum_{i=1}^{k-1}(cT_i-X_i)<0\right){\rm d}F(x)\lambda e^{-\lambda t}{\rm d}t . \end{aligned} \]

(4) 由 \(\psi_{k-1}(u-x+ct)\leq e^{-R(u-x+ct)}\) 可得

\[\begin{aligned} \psi_k(u)&\leq\int_0^\infty\int_0^\infty e^{-R(u-x+ct)}{\rm d}F(x)\lambda e^{-\lambda t}{\rm d}t \\ \\ &=e^{-Ru}\int_0^\infty \lambda e^{-t(\lambda+Rc)}{\rm d}t\int_0^\infty e^{Rx}{\rm d}F(x) \\ \\ &=e^{-Ru}\frac{\lambda}{\lambda+cR}m_X(R) \\ \\ &=e^{-Ru}. \end{aligned} \]

这里最后一个等号用到了 \(\lambda+cR=m_X(R)\) 。

由数学归纳法可知 \(\psi_k(u)\leq e^{-Ru}\) 对每一个 \(k=0,1,\cdots\) 成立。令 \(k\to\infty\) 可知原不等式成立。

推论：正的调节系数意味着破产概率是不确定的，即当 \(R>0\) 时，生存概率是严格正的，

\[\delta(u)=1-\psi(u)>0 ,\quad \forall u\geq0. \]

由于直到时刻 \(1\) 没有理赔发生的概率为 \(e^{-\lambda}>0\) ，根据 Lundberg 定理可知 \(\psi(c)\leq e^{-Rc}\) 。

所以对任何非负初始资本金 \(u\geq0\) ，都有

\[\delta(u)=1-\psi(u)\geq1-\psi(0)\geq e^{-\lambda}\left(1-e^{-Rc}\right)>0. \]