现代精算风险理论05:再保险与最优再保险
第五讲 再保险与最优再保险
第一节 再保险问题
一、再保险的定义和分类
随着社会经济的发展,一次事故可能造成的物质损毁和人身死亡的损失程度不断扩大。若巨额损失由单个保险人来履行赔偿责任,很可能造成保险人的财务困难,甚至因此破产。事实上,任何国家的保险监管机构也不允许保险人单独承担超过其支付能力范围的巨额风险。
我国《保险法》第一百零三条规定:保险公司对每一危险单位,即对一次保险事故可能造成的最大损失范围所承担的责任,不得超过其是有资本金加公积金总和的百分之十;超过的部分应当办理再保险。
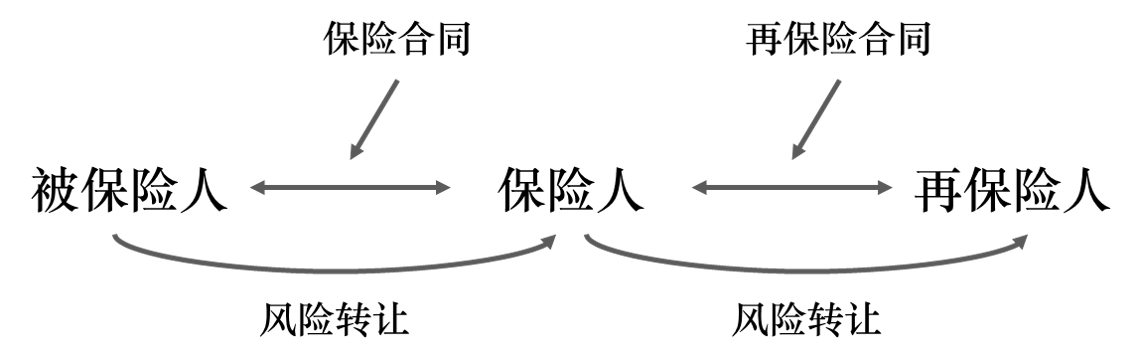
再保险的含义:再保险也称分保,是保险公司在保险合同的基础上,通过签订分保合同的方式,将其承担的保险业务,以承保形式,部分转移给其他保险人。
再保险的目的:进行再保险,可以分散保险人的风险,有利于其控制损失,稳定经营。
再保险的核心:责任转移是再保险的核心所在。
再保险的功能:
- 第一,分散危险责任。任何保险人的资金和承受风险的能力都是有限的。为了保持保险业务正常经营和保险人的财务稳定。避免承保的风险过于集中,对于超过原保险人自身承受能力的风险,原保险人通过再保险,在同业之间相互分散风险。
- 第二,扩大承保能力。随着社会财富积聚,巨额风险增多。保险人有时要承保的保险标的保险金额很高,如大型飞机、核电站、万吨油轮等等,一旦发生事故,其赔偿责任决不是某个保险人所能承担的。在这种情况下,保险人通过再保险,将风险分散于多个保险公司,提高了保险人的承保能力,使原保险人能够以有限的资金接受更高额的风险。
再保险的分类:再保险是在原保险基础上进一步分散风险,是风险的第二次分散。
- 按责任限额,再保险可分为:
- 比例再保险:以保险金额为基础确定分出公司自留额和接受公司责任额的再保险方式。
- 非比例再保险:以损失为基础来确定再保险当事人双方的责任。
- 按安排方式,再保险可分为:
- 临时再保险:将分出业务的具体情况和分保条件逐笔告诉对方,对方是否接受或接受条件完全可以自由选择。
- 合同再保险:双方事先通过契约将业务范围、地区范围、除外责任、佣金、自留额、合同限额、帐单的编制与发送等。各项分保条件用文字固定,明确双方权利与义务。对双方有强制性。
- 预约再保险:对分出公司是临时再保险,对分入公司则是合同再保险。
二、各类再保险形式的特点
比例再保险:又称为金额再保险,以保险金额为基础确定分出公司自留额和接受公司责任额的再保险方式,其特点为:
- 自留额和分保责任额表示为保额的一定比例;
- 双方对于保费和赔款的分配,按照其分配保额的同一比例进行;
- 显示了保险人与再保险人利益的一致性。
比例再保险可分为三类:成数再保险、溢额再保险和混合再保险。
成数再保险:原保险人将每一危险单位的保险金额,按约定的比率分给再保险人的方式,其特点为
- 保额、保费按一定百分比分出,赔款按同样百分比摊回;
- 对每一危险单位有限额规定,分出公司和接受公司在这个限额中各自承担一定的份额。
溢额再保险:双方签订协议,对每一危险单位确定一个由保险人承担的自留额,保险金额超过自留额的部分称为溢额,由再保险人承担,其特点为:
- 以保险金额为基础,自留额确定,不随保险金额变化,自留额内无需分保,超过自留额部分由溢额再保险吸收承受。
- 以自留额的一定倍数为限度称为线数:分出额 \(/\) 自留额 \(=\) 线数。危险单位、自留额和线数称为三要素。
成数和溢额混合再保险:将成数再保险和溢额再保险组织在一个合同里,以成数再保险的限额,作为溢额再保险的起点,再确定溢额再保险的限额。
例如:如果采用成数再保险:最高限额为 \(1000\) 万货运合同,自留 \(20\%\) ,分出 \(80\%\) 。
- 货运 \(A\) 合同:\(500\) 万,自留 \(100\) 万,分出 \(400\) 万,出险后责任比例 \(1:4\) 。
- 货运 \(B\) 合同:\(1000\) 万,自留 \(200\) 万,分出 \(800\) 万,出险后责任比例 \(1:4\) 。
- 货运 \(C\) 合同:\(1500\) 万,自留 \(200\) 万,分出 \(800\) 万,另有 \(500\) 万列入其他的合同或自留,出险后责任比例 \(7:8\)
例如:如果采用溢额再保险:自留额为 \(300\) 万,溢额分保限额为 \(10\) 线。
- 货运 \(A\) 合同:\(500\) 万,自留 \(300\) 万,分出 \(200\) 万,出险后责任比例 \(3:2\) 。
- 货运 \(B\) 合同:\(1000\) 万,自留 \(300\) 万,分出 \(700\) 万,出险后责任比例 \(3:7\) 。
- 货运 \(C\) 合同:\(4000\) 万,自留 \(300\) 万,分出 \(3000\) 万,另有 \(700\) 万列入其他的合同或自留,出险后责任比例为 \(1:3\) 。
非比例再保险:以损失或索赔额为基础来确定再保险当事人双方的责任,其具有两个限额:
- 自负责任额:分出公司根据自身财力确定,即分保合同的起赔点。
- 再保险责任额:接受公司承担的最高责任额。
非比例再保险可分为三类:超额赔款再保险、停止损失再保险和最大赔款再保险。
超额赔款再保险:以每一危险所发生的赔款来计算自负责任额和再保险责任额,其特点为:
- 对原保险人因同一原因发生的任何一次损失或因同一原因导致的各次赔偿的总和超过约定的自付额时,其超出部分有接受公司负责至一定的额度。
- 再保险责任额有一定限度。
停止损失再保险:和超额赔款再保险类似,区别在于超额赔款再保险以单个风险或一次事故为理赔基础,而停止损失再保险是以原保险人一段时间(一般为一年)的总损失为理赔基金。停止损失再保险,合约中也要规定自留额和赔偿限额。
超额赔款再保险和停止损失再保险可以用以下两个公式加以区分:
最大赔款再保险:指的是再保险人承担一年内金额最高的若干次索赔额,其余事故再保险人不再承担赔偿责任。
三、常见再保险的形式
从理论的角度来看,实际最常见的再保险的形式可以归纳为如下几类函数:
-
比例再保险(Quota-share):
\[f(x)=cx,\quad 0\leq c\leq 1. \] -
停止损失再保险(Stop-loss):
\[f(x)=(x-d)_+,\quad d\geq0. \] -
乘数再保险(Change-loss):
\[f(x)=c(x-d)_+,\quad 0\leq c\leq 1,\quad d\geq0. \] -
限额停止损失再保险:设 \(M\) 为最大限额,
\[f(x)=\min\{(x-d)_+,M\}. \]
第二节 最优再保险
一、再保险模型
最优再保险是指在某种意义下,选择一个最优的再保险合同或再保险形式。
一般来说,最优再保险中的“最优”包括以下两类:
- 在保证保险公司的效用或收益的条件下,使保险公司的风险达到最小;
- 将风险控制在一定的范围内,使保险公司的效用或收益达到最大。
再保险模型:主要包括以下三个方面:
- 假设保险公司承担了一个风险 \(X\) ,可以看成是一个随机变量。
- 保险公司将风险的一部分 \(f(X)\) 转移给再保险公司或另一家保险公司,这里 \(f(x)\) 可以看成是一个函数,满足 \(0\leq f(x)\leq x\) 。
- 保险公司自留风险部分为 \(I(X)=X-f(X)\) ,由于向再保险公司转移了部分风险,因此,必须要向其支付一定的保费 \(\Pi(f(X))\) 。
从风险角度考虑,再保险后,保险公司所承担的风险为
其中 \(\Pi(\cdot)\) 为再保险保费计算原理。
如果采用风险度量 \(\rho(\cdot)\) 来度量保险公司所承担的风险,则有
从效用角度考虑,假设保险公司财富为 \(W\) ,承担了一个风险 \(X\) ,并收取了保费为 \(P\) 。再保险后,保险公司的财富为
如果采用效用函数 \(u(\cdot)\) 来刻画再保险对保险公司效用,则有
特别地,如果 \(u(x)=x\) ,则 \(u(T'(X))\) 表示收益。
从风险和效用两个角度考虑,最优再保险模型可以分为风险极小化模型和效用极大化模型。
风险极小化模型:控制效用或收益超过某个设定的值,找一个最优的函数 \(f^*(x)\) ,使 \(\rho(T(X))\) 达到极小值,即
效用极大化模型:控制风险在一定范围内,找一个最优的函数 \(f^*(x)\) ,使 \(\mathbb{E}[u(T'(x))]\) 达到极大值,即
例如:假设 \(S\) 是一个聚合风险,服从复合泊松分布,参数为 \(\lambda\) ,索赔额 \(X\) 的分布函数为 \(F(x)\) ,其对应的密度函数为 \(p(x)\) 。
现以比例再保险的方式进行分保,即分保风险为 \((1-a)S\) ,自留风险为 \(aS\) ,即
\[\begin{aligned} &f(S)=(1-a)S=(1-a)\sum_{i=1}^NX_i, \\ \\ &T'(S)=W+P-a\sum_{i=1}^NX_i-\Pi\left[(1-a)\sum_{i=1}^NX_i\right], \end{aligned} \]采用指数保费计算原理,风险厌恶系数为 \(A\) ,则再保险保费为
\[P_{R}=\Pi\left[(1-a)\sum_{i=1}^NX_i\right]=\frac1A\ln\mathbb{E}\left[e^{(1-a)AS}\right]=\frac1A\lambda\left[m_S((1-a)A)-1\right]. \]采用指数效用,风险厌恶系数为 \(\beta\) ,\(u(x)=-\beta e^{-\beta x}\) ,使得再保险后指数效用极大,有
\[\begin{aligned} \mathbb{E}[u(T'(S))]&\propto-\beta\exp\left\{\beta P_R\right\}\mathbb{E}\left[\exp\left\{\beta a\sum_{i=1}^NX_i\right\}\right] \\ \\ &=-\beta\exp\left\{\frac{\beta \lambda}{A}\left[m_S((1-a)A)-1\right]+\lambda(m_S(a\beta)-1)\right\}. \end{aligned} \]极大化 \(\mathbb{E}[u(T'(S))]\) ,即使得
\[\frac{\mathrm{d}\mathbb{E}[u(T'(S))]}{\mathrm{d}a}=0 \quad \Longrightarrow \quad m_S((1-a)A)=m_S(a\beta) . \]解得
\[(1-a)A=a\beta \quad \Longrightarrow \quad a=\frac{A}{A+\beta}. \]所以采用以比例再保险的方式进行分保,出险后责任比例为
\[\text{自留}:\text{分出}=\frac{a}{1-a}=\frac{A}{\beta}. \]
例如:假设 \(S\) 是一个聚合风险,服从复合泊松分布,参数为 \(\lambda\) ,索赔额 \(X\) 的分布函数为 \(F(x)\) ,其对应的密度函数为 \(p(x)\) 。
现以限额停止损失再保险的方式进行分保,即分保风险为 \([X-M]_+\) ,自留风险为 \(\min\{X,M\}\) ,即
\[\begin{aligned} &f(S)=\sum_{i=1}^N[X_i-M]_+, \\ \\ &T'(S)=W+P-\sum_{i=1}^N\min\{X_i,M\}-\Pi\left[\sum_{i=1}^N[X_i-M]_+\right], \end{aligned} \]采用均值保费计算原理,则再保险保费为
\[P_R=\Pi\left[\sum_{i=1}^N[X_i-M]_+\right]=(1+\theta)\lambda\mathbb{E}\left[X_i-M\right]_+. \]采用指数效用,风险厌恶系数为 \(\beta\) ,\(u(x)=-\beta e^{-\beta x}\) ,使得再保险后指数效用极大,有
\[\begin{aligned} \mathbb{E}[u(T'(S))]\propto\;&-\exp\left\{-(1+\theta)\lambda\beta\int_M^\beta(x-M)f(x){\rm d}x\right\} \\ &\times \exp\left\{\lambda\int_0^Me^{-\beta x}f(x){\rm d}x+\lambda e^{-\beta M}\right\}. \end{aligned} \]极大化 \(\mathbb{E}[u(T'(S))]\) ,即使得
\[\frac{\mathrm{d}\mathbb{E}[u(T'(S))]}{\mathrm{d}M}=0 \quad \Longrightarrow \quad (1+\theta)=e^{-\beta M} . \]解得
\[M=\frac1\beta\ln(1+\theta). \]
二、最优再保险的基本定理
比例再保险和停止损失再保险是最重要的两种再保险的形式,主要由下面两个最优再保险的基本定理保证其最优性。
定理(停止损失再保险的最优性):假设 \(\mathbb{E}[X-f(X)]=c\) ,则
即对于风险极小化模型
该模型的最优解为 \(f^*(X)=(X-d)_+\) 。
说明:如果在自留风险的收益均值相等的假设下,停止损失再保险使自留风险的方差达到最小。
因为自留风险收益相等,即
\[\mathbb{E}[X-f(X)]=\mathbb{E}[X-(X-d)_+], \]故只需证
\[\mathbb{E}[X-f(X)]^2\geq\mathbb{E}[X-(X-d)_+]^2. \]记 \(V(X)=X-f(X),\ W(X)=X-(X-d)_+\) ,故只需证
\[\mathbb{E}[V(X)-d]^2\geq\mathbb{E}[W(X)-d]^2. \]当 \(X\geq d\) 时,\((X-d)_+=X-d\) ,所以 \(W(X)-d=0\) ,所以
\[|V(X)-d|\geq|W(X)-d|=0. \]当 \(X<d\) 时,\(W(X)=X\) ,所以
\[V(X)-d=X-f(X)-d=(X-d)-f(X)\leq X-d=W(X)-d<0. \]故 \(|V(X)-d|>|W(X)-d|\) 。
综上,则有
\[\mathbb{E}[V(X)-d]^2\geq\mathbb{E}[W(X)-d]^2. \]
定理(比例再保险的最优性):假设 \({\rm Var}[X-f(X)]=V\) ,假设保费计算方式如下:
-
保险合同收取的保费采用均值保费计算原理,即
\[\Pi(X)=(1+\lambda)\mathbb{E}(X). \] -
再保险合同的保费采用均值方差计算原理,即
\[\Pi(X)=\mathbb{E}[f(X)]+\beta{\rm Var}[f(X)]. \]
则使保险公司在再保险后能有最大收益的最优再保险的形式为比例再保险。
再保险前,保险公司的收益为
\[(1+\lambda)\mathbb{E}(X)-X. \]再保险后,保险公司的收益为
\[(1+\lambda)\mathbb{E}(X)-X+f(X)-\mathbb{E}[f(X)]-\beta{\rm Var}[f(X)]. \]故再保险后的期望收益为
\[\mathbb{E}\left[(1+\lambda)\mathbb{E}(X)-X+f(X)-\mathbb{E}[f(X)]-\beta{\rm Var}[f(X)]\right]=\lambda\mathbb{E}(X)-\beta{\rm Var}[f(X)]. \]收益极大化模型为
\[\left\{\begin{array}{cl} \displaystyle\max_{0\leq f(x)\leq x}& \lambda\mathbb{E}(X)-\beta{\rm Var}[f(X)], \\ \\ {\rm s.t.}& {\rm Var}[X-f(X)]=V , \end{array}\right. \]由于
\[\begin{aligned} {\rm Var}[f(X)]&={\rm Var}[X-(X-f(X))] \\ \\ &={\rm Var}(X)-2{\rm Cov}(X,X-f(X))+{\rm Var}(X-f(X)) \\ \\ &=V+{\rm Var}(X)-2{\rm Cov}(X,X-f(X)). \end{aligned} \]要使得 \({\rm Var}[f(X)]=V+{\rm Var}(X)-2{\rm Cov}(X,X-f(X))\) 达到极小,注意当 \(X\) 和 \(X-f(X)\) 完全线性正相关时,\({\rm Var}[f(X)]\) 达到极小,收益极大。
完全线性正相关可以用 \(X-f(X)=a+bX\) 来表示,其中 \(b>0\) ,即 \(f(X)=-a+(1-b)X\) 。
由 \(0\leq -a+(1-b)X\leq X\) 可知 \(a=0\) ,进而由 \(0\leq(1-b)X\leq X\) 可知 \(0\leq b\leq 1\) 。
所以 \(f(X)\) 的表达式为
\[f(X)=(1-b)X,\quad 0\leq b\leq 1. \]
定理:设某个保险人的效用函数为 \(u(\cdot)\) ,且满足 \(u'(x)\geq0\) 和 \(u''(x)<0\) ,如果在制定分保计划时采用效用极大化模型,并假设
- 保险人具有初始准备金为 \(w\) ;
- 一段时间内总损失为 \(X\) ;
- 保险人用于分保的保费为 \(c\) ;
- 再保险人采用均值保险计算原理收取保费,即 \(\Pi(X)=(1+\lambda)\mathbb{E}(X)\) ,
则采用停止损失再保险能够使效用达到最大,即 \(f(X)=[X-d]_+\) 。
该定理和第四讲的最优保险问题等同。


