现代精算风险理论03：聚合风险模型

目录

• 第三讲 聚合风险模型
  • 第一节 聚合风险的分布
    • 一、定义和假设
    • 二、聚合风险的数字特征
    • 三、复合泊松分布
  • 第二节 Panjer 递推
    • 一、Panjer 递推的定义
    • 二、复合泊松分布的 Panjer 递推
  • 第三节 停止损失保费
    • 一、停止损失保费的定义
    • 二、Panjer 递推与停止损失保费
    • 三、案例

第三讲 聚合风险模型

第一节 聚合风险的分布

一、定义和假设

一般聚合风险模型需要考虑时间的因素，因此也往往会考虑利率的因素。为了简化模型，本节虽然考虑在某个时间段内理赔总额的分布函数，但不考虑利率的因素。

聚合风险模型把风险组合理解为在一定时间段内产生的随机多个理赔的全体，定义

\[S_N=X_1+X_2+\cdots+X_N, \]

其中 \(N\) 表示理赔次数，\(X_i\ (i=1,2,\cdots,N)\) 表示第 \(i\) 个理赔额。约定当 \(N=0\) 时，\(S_N=0\) 。

聚合风险模型其本质是随机变量的随机和，或者说是一个复合分布。聚合风险模型和个体风险模型的差异主要有以下两点：

• 在个体风险模型中 \(X_i\) 可能为 \(0\) ，在聚合风险模型中一般 \(X_i>0\) ；
• 在个体风险模型中理赔次数 \(n\) 是确定值，在聚合风险模型中理赔次数 \(N\) 是一个随机变量。

聚合风险模型的基本假设为：

• 个体理赔额 \(X_i\ (i=1,2,\cdots,N)\) 是独立同分布的，记为与 \(X\) 同分布。
• 索赔次数 \(N\) 是取值为自然数的离散型随机变量。特别地，
  • 当 \(N\) 服从泊松分布时，称 \(S_N\) 服从复合泊松分布；
  • 当 \(N\) 服从二项分布时，称 \(S_N\) 服从复合二项分布；
  • 当 \(N\) 服从负二项分布时，称 \(S_N\) 服从复合负二项分布；
  • 当 \(N\) 服从几何分布时，称 \(S_N\) 服从复合几何分布。
• 个体理赔额 \(X_i\ (i=1,2,\cdots,N)\) 与索赔次数 \(N\) 相互独立。

二、聚合风险的数字特征

对于聚合风险模型的总理赔额 \(S_N\) 和个体理赔额 \(X_i\ (i=1,2,\cdots,N)\) ，记

\[\mu_k=\mathbb{E}\left[X^k\right],\quad P(x)=\mathrm{Pr}(X\leq x),\quad F(s)=\mathrm{Pr}(S_N\leq s). \]

利用全期望公式和方差分解准则可以计算总理赔额 \(S_N\) 的期望、方差和矩母函数：

全期望公式：

\[\mathbb{E}(W)=\mathbb{E}[\mathbb{E}(W|V)]. \]

方差分解准则：

\[{\rm Var}(W)={\rm Var}[\mathbb{E}(W|V)]+\mathbb{E}[{\rm Var}(W|V)]. \]

计算 \(S_N\) 的期望：

\[\begin{aligned} \mathbb{E}(S_N)&=\mathbb{E}\left[\mathbb{E}(S_N|N)\right] \\ \\ &=\sum_{n=0}^\infty\mathbb{E}[X_1+X_2+\cdots+X_N|N=n]\mathrm{Pr}(N=n) \\ \\ &=\mathbb{E}(X)\sum_{n=0}^\infty n{\rm Pr}(N=n) \\ \\ &=\mu_1\mathbb{E}(N). \end{aligned} \]

计算 \(S_N\) 的方差：

\[\begin{aligned} {\rm Var}(S_N)&={\rm Var}[\mathbb{E}(S_N|N)]+\mathbb{E}[{\rm Var}(S_N|N)] \\ \\ &={\rm Var}(N\mu_1)+\mathbb{E}[N{\rm Var}(X)] \\ \\ &=\mu_1^2{\rm Var}(N)+\mathbb{E}(N){\rm Var}(X). \end{aligned} \]

计算 \(S_N\) 的矩母函数：

\[\begin{aligned} m_S(t)&=\mathbb{E}\left[e^{tS_N}\right] \\ \\ &=\mathbb{E}\left[\mathbb{E}[e^{tS_N}|N]\right] \\ \\ &=\mathbb{E}\left[\mathbb{E}\left[e^{t(X_1+X_2+\cdots+X_N)}\big|N\right]\right] \\ \\ &=\mathbb{E}\left[\left(m_X(t)\right)^N\right] \\ \\ &=\mathbb{E}\left[e^{N\cdot\log m_X(t)}\right] \\ \\ &=m_N\left(\log m_X(t)\right). \end{aligned} \]

例如：复合几何分布的分布函数

假设理赔次数 \(N\sim G(p), \ 0<p<1\) ，随机变量 \(X\sim \mathrm{Exp}(\theta)\) 。求该复合几何分布 \(S_N\) 的分布。

解题思路：首先计算 \(S_N\) 的矩母函数，然后尝试通过矩母函数来确定该复合分布。

由 \(N\sim G(p)\) 可知，记 \(q=1-p\) ，当 \(q e^t<1\) 时，即当 \(t<-\log q\) 时，

\[m_N(t)=\sum_{n=0}^\infty e^{tn}pq^n=\frac{p}{1-qe^t}. \]

由 \(X\sim \mathrm{Exp}(\theta)\) 可知

\[m_X(t)=\frac{\theta}{\theta-t} \ , \quad 0<t<\theta. \]

所以 \(S_N\) 的矩母函数为

\[\begin{aligned} m_S(t)&=m_N(\log m_X(t)) \\ \\ &=\frac{p}{1-qm_X(t)} \\ \\ &=\frac{p}{1-\dfrac{q\theta}{\theta-t}} \\ \\ &=\frac{p(\theta-t)}{\theta p-t} \\ \\ &=p+q\frac{\theta p}{\theta p-t}. \end{aligned} \]

可见 \(S_N\) 的矩母函数是常数 \(0\) 的矩母函数与 \({\rm Exp}(\theta p)\) 分布的矩母函数的一个混合。

由分布函数与矩母函数之间的一一对应关系可知，\(S_N\) 的分布函数也具有同样的混合结构：

\[S_N\xlongequal{d}IX+(1-X)Y. \]

其中 \(I\sim B(1,p), \ X=0 , \ Y\sim \mathrm{Exp}(\theta p)\) 。于是 \(S_N\) 的分布函数为

\[F(x)=p+q(1-e^{-\theta px})=1-qe^{-\theta px} , \quad x\geq0. \]

分布函数 \(F(x)\) 在 \(0\) 点有跳跃，高度为 \(p\) ，而当 \(x>0\) 时，\(F(x)\) 服从指数分布。

三、复合泊松分布

复合泊松分布的数字特征

假设理赔次数 \(N\sim P(\lambda)\) ，随机变量 \(X\) 的各阶矩记为 \(\mathbb{E}(X^k)=\mu_k\) ，矩母函数记为 \(m_X(t)\) 。

复合泊松分布 \(S_N\) 的均值和方差：

\[\begin{aligned} &\mathbb{E}(S_N)=\mu_1\mathbb{E}(N)=\lambda\mu_1. \\ \\ &\begin{aligned} {\rm Var}(S_N)&= \mu_1^2{\rm Var}(N)+\mathbb{E}(N){\rm Var}(X) \\ \\ &=\lambda\mu_1^2+\lambda(\mu_2-\lambda_1^2) \\ \\ &=\lambda\mu_2. \end{aligned} \end{aligned} \]

复合泊松分布 \(S_N\) 的矩母函数：

\[m_N(t)=\exp\left\{\lambda(e^t-1)\right\}, \\ \\ m_{S}(t)=m_N(\log m_X(t))=\exp\left\{\lambda(m_X(t)-1)\right\}. \]

复合泊松分布 \(S_N\) 的累积量母函数：

\[\kappa_S(t)=\log m_S(t)=\lambda(m_X(t)-1)=\lambda\sum_{k=1}^\infty\mu_k\frac{t^k}{k!}. \]

复合泊松分布 \(S_N\) 的三阶中心矩：

\[\mathbb{E}\left[(S_N-\mathbb{E}(S_N))^3\right]=\frac{\mathrm{d}^3}{\mathrm{d}t^3}\kappa_S(t)\bigg|_{t=0}=\lambda\mu_3. \]

复合泊松分布的近似分布

设 \(S_N\) 服从复合泊松分布，其参数为 \(\lambda\) ，记理赔额 \(X\) 的 \(k\) 阶矩为 \(\mu_k\) ，则有

\[\mu_{S}=\mathbb{E}(S_N)=\lambda\mu_1, \quad \sigma_S^2={\rm Var}(S_N)=\lambda\mu_2 , \\ \\ \gamma_S=\frac{\lambda\mu_3}{(\sqrt{\lambda\mu_2})^3}=\frac{\mu_3}{\mu_2^{3/2}\sqrt{\lambda}}. \]

复合泊松分布的中心极限定理：

\[\lim_{\lambda\to\infty}\mathrm{Pr}\left[\frac{S_N-\lambda\mu_1}{\sqrt{\lambda\mu_2}}\leq x\right]=\Phi(x) . \]

复合泊松分布的平移伽马近似：

\[\begin{aligned} &\alpha=\frac{4}{\gamma_S^2}=\frac{4\lambda\mu_2^3}{\mu_3^2}, \\ \\ &\beta=\frac{2}{\gamma_S\sigma_S}=\frac{2\mu_2}{\mu_3},\\ \\ &x_0=\mu_S-\frac{2\sigma_S}{\gamma_S}=\lambda\mu_1-\frac{2\lambda\mu_2^2}{\mu_3}. \end{aligned} \]

复合泊松分布的 NP 近似：

当 \(s\geq1\) 时，

\[\mathrm{Pr}\left[\frac{S_N-\mu_S}{\sigma_S}\leq s+\frac{\gamma_S}{6}(s^2-1)\right]\approx\Phi(s). \]

当 \(x\geq1\) 时，

\[\mathrm{Pr}\left[\frac{S_N-\mu_S}{\sigma_S}\leq x\right]\approx\Phi\left(\sqrt{\frac{9}{\gamma_S^2}+\frac{6x}{\gamma_S}+1}-\frac{3}{\gamma_S}\right). \]

定理（复合泊松分布的和仍是复合泊松分布）如果 \(S_1,S_2,\cdots,S_m\) 是一列独立的复合泊松分布的随机变量，分别具有参数 \(\lambda_i\) 和理赔分布 \(P_i(x)\ (i=1,2,\cdots,m)\) ，那么 \(S=S_1+S_2+\cdots+S_m\) 仍是一个复合泊松分布的随机变量，其参数和理赔分布分别为

\[\lambda=\sum_{i=1}^m\lambda_i , \quad P(x)=\sum_{i=1}^m\frac{\lambda_i}{\lambda}P_i(x). \]

设 \(m_i(x)\) 是 \(P_i(x)\) 的矩母函数，则 \(S\) 的矩母函数为

\[m_S(t)=\prod_{i=1}^m\exp\left\{\lambda_i\left[m_i(t)-1\right]\right\}=\exp\left\{\lambda\left[\sum_{i=1}^m\frac{\lambda_i}{\lambda}m_i(t)-1\right]\right\}. \]

故 \(S\) 是一个复合泊松随机变量。

该定理常用于解释以下两个情景：

• 对任意 \(m\) 个独立复合泊松风险组合，其总和仍然服从复合泊松分布；
• 对同一个复合泊松风险组合观测 \(m\) 年且假设每年的结果相互独立，则 \(m\) 年结果的总和仍然服从复合泊松分布。

定理（理赔次数服从独立泊松分布） 假设 \(S\) 服从参数为 \(\lambda\) 的复合泊松分布，其中理赔分布是一个离散型分布，且满足

\[\pi_i=p(x_i)=\mathrm{Pr}(X=x_i) , \quad i=1,2,\cdots,m. \]

如果 \(S\) 可以表示成

\[S=x_1N_1+x_2N_2+\cdots+x_mN_m, \]

其中 \(N_i\) 表示理赔额 \(x_i\) 的发生次数，则 \(N_1,N_2,\cdots,N_m\) 构成一列独立的 \(P(\lambda\pi_i)\ (i=1,2,\cdots,m)\) 随机变量。

引理：多项分布

某随机试验有 \(k\) 个可能的结果 \(A_1,A_2,\cdots,A_k\) ，它们可能出现的概率分别为 \(p_1,p_2,\cdots,p_k\) 。将它们出现的次数记为随机变量 \(X_1,X_2,\cdots,X_k\) 。

在 \(n\) 次试验结果中，\(A_i\) 出现 \(n_i\) 次 \((i=1,2,\cdots,k)\) ，其中 \(n_1+n_2+\cdots+n_k=n\) ，这种事件发生的概率为

\[\mathrm{Pr}(X_1=n_1,X_2=n_2,\cdots,X_k=n_k)=\frac{n!}{n_1!n_2!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_k^{n_k}. \]

随机向量 \((X_1,X_2,\cdots,X_k)\) 的分布称为多项分布，记为 \(M(n,p_1,p_2,\cdots,p_k)\) 。

记 \(N=N_1+N_2+\cdots+N_m\) 和 \(n=n_1+m_2+\cdots+n_m\) ，对 \(N=n\) 取条件得

\[(N_1,N_2\cdots,N_m|N=n)\sim M(n,\pi_1,\pi_2,\cdots,\pi_m) , \]

于是

\[\begin{aligned} &\mathrm{Pr}(N_1=n_1,N_2=n_2,\cdots,N_m=n_m) \\ \\ =\; & \mathrm{Pr}(N_1=n_1,N_2=n_2,\cdots,N_m=n_m|N=n)\mathrm{Pr}(N=n) \\ \\ =\; & \frac{n!}{n_1!n_2!\cdots n_m!}\pi_1^{n_1}\pi_2^{n_2}\cdots \pi_m^{n_m} e^{-\lambda}\frac{\lambda^n}{n!} \\ \\ =\; &\prod_{i=1}^me^{-\lambda\pi_i}\frac{(\lambda\pi_i)^{n_i}}{n_i!} \\ \\ =\; &\mathrm{Pr}(N_1=n_1)\mathrm{Pr}(N_2=n_2)\cdots\mathrm{Pr}(N_m=n_m). \end{aligned} \]

所以 \(N_i\sim P(\lambda\pi_i), \ i=1,2,\cdots,m\) 且相互独立。

第二节 Panjer 递推

一、Panjer 递推的定义

定理（Panjer 递推）考虑这样一个复合分布，满足：

(1) 理赔额 \(X_k\ (k\geq1)\) 独立同分布，取值为自然数，且具有 \(\mathrm{Pr}(X=x)=p(x), \ x=0,1,2,\cdots\) ；

(2) 理赔次数 \(N\) 属于 \((a,b,0)\) 族，即对于实数 \(a\) 和 \(b\) ，事件”有 \(n\) 个理赔发生“的概率 \(q_n=\mathrm{Pr}(N=n)\) 满足如下的递推关系式：

\[q_n=\left(a+\frac bn\right)q_{n-1} , \quad n=1,2,\cdots, \]

则事件“总理赔额等于 \(s\) “的概率 \(f(s)=\mathrm{Pr}(S_N=s)\) 满足如下的关系式：

\[\begin{aligned} &f(0)=\left\{\begin{array}{ll} \mathrm{Pr}(N=0) , & p(0)=0, \\ \\ m_N(\log p(0)), & p(0)>0, \end{array}\right. \\ \\ &f(s)=\frac{1}{1-ap(0)}\sum_{h=1}^s\left(a+\frac{bh}{s}\right)p(h)f(s-h),\quad s=1,2,\cdots. \end{aligned} \]

(1) 计算初始值 \(f(0)\) ：

\[f(0)=\mathrm{Pr}(S=0)=\sum_{n=0}^\infty\mathrm{Pr}(N=n)\left[p(0)\right]^n. \]

当 \(p(0)=0\) 时，

\[f(0)=\mathrm{Pr}(S=0)=\mathrm{Pr}(N=0). \]

当 \(p(0)>0\) 时，

\[f(0)=\mathrm{Pr}(S=0)=\sum_{n=0}^\infty\mathrm{Pr}(N=n)\left[p(0)\right]^n=m_N(\log p(0)). \]

(2) 记 \(T_k=X_1+X_2+\cdots+X_k,\ k\geq1, \ T_0=0\) 。 由对称性可得

\[\mathbb{E}\left[X_1|T_k=s\right]=\frac{s}{k}, \]

所以

\[\mathbb{E}\left[a+\frac{bX_1}{s}\bigg|T_k=s\right]=a+\frac{b}{k}. \]

(3) 另一方面，

\[\begin{aligned} \mathbb{E}\left[a+\frac{bX_1}{s}\bigg|T_k=s\right]&=\sum_{h=0}^s\left( a+\frac{bh}{s}\right)\mathrm{Pr}(X_1=h|T_k=s) \\ \\ &=\sum_{h=0}^s\left( a+\frac{bh}{s}\right)\frac{\mathrm{Pr}(X_1=h,T_k=s)}{\mathrm{Pr}(T_k=s)} \\ \\ &=\sum_{h=0}^s\left( a+\frac{bh}{s}\right)\frac{\mathrm{Pr}(X_1=h)\mathrm{Pr}(T_k-X_1=s-h)}{\mathrm{Pr}(T_k=s)}. \end{aligned} \]

所以

\[\left(a+\frac{b}{k}\right)\mathrm{Pr}(T_k=s)=\sum_{h=0}^s\left( a+\frac{bh}{s}\right){\mathrm{Pr}(X_1=h)\mathrm{Pr}(T_k-X_1=s-h)}. \]

(4) 对任意的 \(s=1,2,\cdots\) ，有

\[\begin{aligned} f(s)&=\sum_{k=1}^\infty q_k\mathrm{Pr}(T_k=s) \\ \\ &=\sum_{k=1}^\infty q_{k-1}\left(a+\frac bk\right)\mathrm{Pr}(T_k=s) \\ \\ &=\sum_{k=1}^\infty q_{k-1}\sum_{h=0}^s\left(a+\frac{bh}{s}\right)\mathrm{Pr}(X_1=h)\mathrm{Pr}(T_k-X_1=s-h) \\ \\ &=\sum_{h=0}^s\left(a+\frac{bh}{s}\right)\mathrm{Pr}(X_1=h)\sum_{k=1}^\infty q_{k-1}\mathrm{Pr}(T_k-X_1=s-h) \\ \\ &=\sum_{h=0}^s\left(a+\frac{bh}{s}\right)p(h)\sum_{k=1}^\infty q_{k-1}\mathrm{Pr}(T_{k-1}=s-h) \\ \\ &=\sum_{h=0}^s\left(a+\frac{bh}{s}\right)p(h)f(s-h) \\ \\ &=ap(0)f(s)+\sum_{h=1}^s\left(a+\frac{bh}{s}\right)p(h)f(s-h). \end{aligned} \]

由此即可解得 Panjer 递推

\[f(s)=\frac{1}{1-ap(0)}\sum_{h=1}^s\left(a+\frac{bh}{s}\right)p(h)f(s-h),\quad s=1,2,\cdots. \]

利用 Panjer 递推计算 \(S_N\) 的概率分布列的优点在于它避免了卷积的计算，但一般来说，\(S_N\) 的概率分布列的递推公式不存在，只有很少的一些分布满足递推关系式。

对于 Panjer 递推存在的 \(S_N\) ，其任意阶矩也可以通过 Panjer 递推进行计算。对于 \(r=1,2,\cdots\) ，有

\[\begin{aligned} \mathbb{E}\left[S_N^r\right]&=\sum_{s=0}^\infty s^rf(s) \\ \\ &=\frac{1}{1-ap(0)}\sum_{s=0}^\infty s^r\sum_{h=1}^s\left(a+\frac{bh}{s}\right)p(h)f(s-h) \\ \\ &=\frac{1}{1-ap(0)}\sum_{s=0}^\infty\sum_{h=1}^s\left(as^r+bhs^{r-1}\right)p(h)f(s-h) \\ \\ &=\frac{1}{1-ap(0)}\sum_{h=1}^\infty\sum_{s=h}^\infty\left(as^r+bhs^{r-1}\right)p(h)f(s-h) \\ \\ &=\frac{1}{1-ap(0)}\sum_{h=1}^\infty p(h)\sum_{t=0}^\infty\left(a(t+h)^r+bh(t+h)^{r-1}\right)f(t). \end{aligned} \]

利用二项展开，有

\[\begin{aligned} \sum_{t=0}^\infty(t+h)^rf(t)&=\sum_{t=0}^\infty\sum_{i=0}^r{r \choose i}t^ih^{r-i}f(t) \\ \\ &=\sum_{i=0}^r{r \choose i}h^{r-i}\sum_{t=0}^\infty t^if(t) \\ \\ &=\sum_{i=0}^r{r \choose i}h^{r-i}\mathbb{E}\left[S_N^i\right]. \end{aligned} \]

因此，有

\[\begin{aligned} \mathbb{E}\left[S_N^r\right]&=\frac{1}{1-ap(0)}\sum_{h=1}^\infty p(h)\left[a\sum_{i=0}^r{r \choose i}h^{r-i}\mathbb{E}\left[S_N^i\right]+bh\sum_{i=0}^{r-1}{r-1 \choose i}h^{r-i-1}\mathbb{E}\left[S_N^i\right]\right] \\ \\ &=\frac{1}{1-ap(0)}\left[a\sum_{i=0}^r{r \choose i}\mathbb{E}\left[S_N^i\right]\sum_{h=1}^\infty h^{r-i}p(h)+b\sum_{i=0}^{r-1}{r-1 \choose i}\mathbb{E}\left[S_N^i\right]\sum_{h=1}^\infty h^{r-i}p(h)\right] \\ \\ &=\frac{1}{1-ap(0)}\left[\sum_{i=0}^{r-1}\left[a{r \choose i}+b{r-1 \choose i}\right]\mathbb{E}\left[S_N^i\right]\mathbb{E}\left[X_1^{r-i}\right]+a\mathbb{E}\left[S_N^r\right]\sum_{h=1}^\infty p(h)\right]. \end{aligned} \]

由于 \(\sum_{k=1}^\infty f_k=1-f_0\) ，对上述等式进行整理可得

\[\mathbb{E}\left[S_N^r\right]=\frac{1}{1-a}\sum_{i=0}^{r-1}\left[a{r \choose i}+b{r-1 \choose i}\right]\mathbb{E}\left[S_N^i\right]\mathbb{E}\left[X_1^{r-i}\right]. \]

二、复合泊松分布的 Panjer 递推

对于 \(N\sim P(\lambda)\) ，有 \(a=0,\ b=\lambda\geq0\) ，并且递推关系可以被简化为

\[\begin{aligned} &f(0)=e^{-\lambda(1-p(0))}, \\ \\ &f(s)=\frac1s\sum_{h=1}^s\lambda hp(h)f(s-h), \quad s=1,2,\cdots. \\ \\ &\mathbb{E}\left[S_N^r\right]=\lambda\sum_{i=0}^{r-1}{r-1 \choose i}\mathbb{E}\left[S_N^i\right]\mathbb{E}\left[X_1^{r-i}\right], \quad r=1,2,\cdots. \end{aligned} \]

利用 Panjer 递推公式也可以求复合泊松分布的前三阶矩：

\[\begin{aligned} &\mathbb{E}(S_N)=\lambda\mathbb{E}(X_1)=\lambda\mu_1. \\ \\ &\mathbb{E}(S_N^2)=\lambda\left[\mathbb{E}(X_1^2)+\mathbb{E}(S_N)\mathbb{E}(X_1)\right]=\lambda\mu_2+\left[\mathbb{E}(S_N)\right]^2. \\ \\ &\begin{aligned} \mathbb{E}(S_N^3)&=\lambda\left[\mathbb{E}(X_1^3)+2\mathbb{E}(S_N)\mathbb{E}(X_1^2)+\mathbb{E}(S_N^2)\mathbb{E}(X_1)\right] \\ \\ &=\lambda\mu_3+2\mathbb{E}(S_N)\left[\mathbb{E}(S_N^2)-\left[\mathbb{E}(S_N)\right]^2\right]+\mathbb{E}(S_N^2)\mathbb{E}(S_N) \\ \\ &=\lambda\mu_3+3\mathbb{E}(S_N^2)\mathbb{E}(S_N)-2\left[\mathbb{E}(S_N)\right] ^3. \end{aligned} \end{aligned} \]

由此也可以推出

\[\begin{aligned} &{\rm Var}(S_N)=\mathbb{E}(S_N^2)-\left[\mathbb{E}(S_N)\right]^2=\lambda\mu_2 , \\ \\ &\mathbb{E}\left[(S_N-\mathbb{E}(S_N))^3\right]=\mathbb{E}(S_N^3)-3\mathbb{E}(S_N^2)\mathbb{E}(S_N)+2\left[\mathbb{E}(S_N)\right]^3=\lambda\mu_3. \end{aligned} \]

第三节 停止损失保费

一、停止损失保费的定义

在保险实务中，为了促使投保人有自我防灾意识，以减少不必要的损失，通常不是全额承包。保险合同规定的赔付额通常低于实际损失。由于理赔额是损失的函数，故常记为 \(I(X)\) ，满足 \(0\leq I(X)\leq X\) 。

有一种简单但特别重要的形式为

\[I_d=\max\{0，X-d\}=(X-d)_{+}, \]

其中 \(d\) 称为免赔额。它的意义是当损失低于免赔额 \(d\) 时不予理赔，只有超过 \(d\) 的部分才予以理赔，其理赔额为 \(X-d\) 。这种形式称为停止损失。

对于停止损失保险合同，其纯保费为 \(\mathbb{E}\left[(X-d)_{+}\right]\) 称为停止损失保费，记为 \(\pi_X(d)=\mathbb{E}\left[(X-d)_{+}\right]\) 。由于停止损失保费是免赔额 \(d\) 的函数，故也称为停止损失函数。

若风险 \(X\) 是连续型随机变量，其密度函数为 \(f_X(x)\) ，假设 \(\mathbb{E}(X)<\infty\) ，则停止损失保费为

\[\pi_X(d)=\int_d^\infty (x-d)f_X(x)\mathrm{d}x. \]

记 \(F_X(x)\) 为随机变量 \(X\) 的分布函数，记 \(\bar{F}_X(x)=1-F(x)\) 为生存函数，则有

\[\pi_X(d)=-(x-d)\bar{F}_X(x)\bigg|_d^\infty+\int_d^\infty\bar{F}_X(x)\mathrm{d}x=\int_d^\infty\bar{F}_X(x)\mathrm{d}x. \]

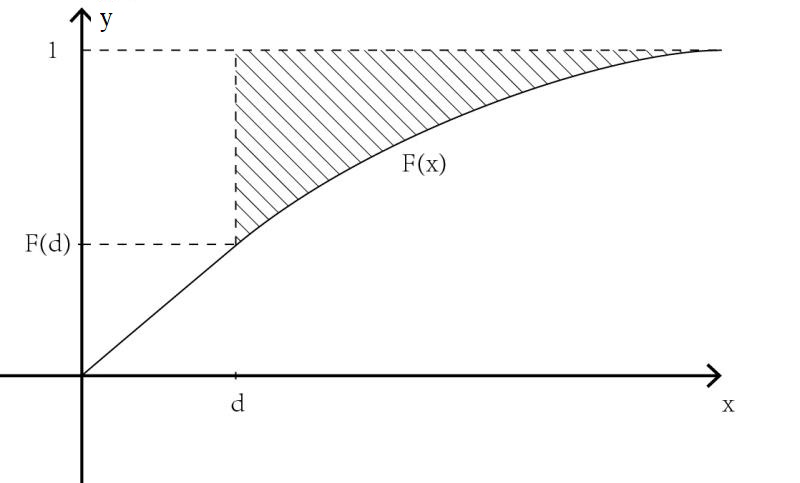
若风险 \(X\) 是连续型随机变量，并且在 \(x\) 处有概率为 \(f_X(x)\) ，则停止损失保费为

\[\pi_X(d)=\sum_{x>d}(x-d)f_X(x). \]

如果 \(X\) 在 \(x_1<x_2<\cdots<x_k<d<x_{k+1}<\cdots\) 处有概率，记分布函数 \(F_X(x)=\mathrm{Pr}(X\leq x)\) ，则有

\[\pi_X(d)=\bar{F}_X(x_{k})(x_{k+1}-d)+\sum_{i=k+1}\bar{F}_X(x_i)(x_{i+1}-x_i)=\int_d^\infty\bar{F}_X(x)\mathrm{d}x. \]

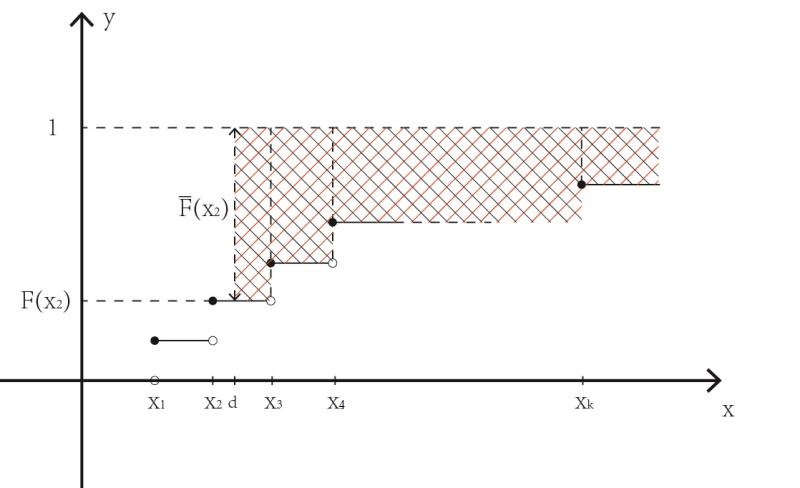
对于任意的风险 \(X\) ，其停止损失函数可以统一表示为

\[\pi_X(d)=\int_d^\infty\bar{F}_X(x)\mathrm{d}x. \]

由停止损失函数可得

\[\pi_X'(d)=F_X(x)-1 , \quad F_X(x)=\pi_X'(d)+1. \]

可以证明停止损失函数与分布函数构成一一对应关系，即两个风险具有相同的停止损失函数，则必有相同的分布函数，反之亦然。

对于任意停止损失函数，满足如下三个条件：

• 停止损失函数 \(\pi_X(d)\) 是一个连续函数；
• 停止损失函数 \(\pi_X(d)\) 关于 \(d\) 严格递减；
• \(\pi_X(0)=\mathbb{E}(X), \ \pi_X(\infty)=0\) 。

如果存在一个函数 \(\pi(\cdot)\) 满足以上三个性质，则称为停止损失函数，并且一定存在一个随机变量 \(X\) ，其停止损失函数恰好为 \(\pi(\cdot)\) 。

二、Panjer 递推与停止损失保费

对于一个整值随机变量 \(S\) ，其停止损失保费可以表示为

\[\pi(d)=\mathbb{E}\left[(S-d)_+\right]=\sum_{x=d}^\infty(x-d)f(x)=\sum_{x=d}^\infty[1-F(x)]. \]

利用 Panjer 递推，停止损失保费也可以通过递推求得，对整数 \(d\geq0\) ，有

\[\begin{aligned} &\pi(0)=\mathbb{E}(S), \\ \\ &\pi(d)=\sum_{x=d}^\infty[1-F(x)]=\pi(d-1)-[1-F(d-1)], \quad d=1,2,\cdots. \end{aligned} \]

假设 \(S\) 服从复合泊松分布，\(N\sim P(1)\) ，其中 \(X_i\) 为两点分布

\[p(1)=p(2)=\frac12. \]

给出停止损失保费的递推公式。

复合泊松分布的 Panjer 递推如下：

\[\begin{aligned} &f(0)=e^{-\lambda(1-p(0))}, \\ \\ &f(s)=\frac1s\sum_{h=1}^s\lambda hp(h)f(s-h), \quad s=1,2,\cdots. \end{aligned} \]

由题意知 \(\lambda=1,\ p(0)=0\) ，因此

\[\begin{aligned} &f(0)=e^{-1}, \\ \\ &f(1)=\frac12f(0)=\frac12e^{-1} , \\ \\ &f(x)=\frac1x\left[\frac12f(x-1)+f(x-2)\right], \quad x=2,3,\cdots. \end{aligned} \]

由题意知 \(\mu_1=\mathbb{E}(X_1)=\dfrac32\) ，初始值为

\[\begin{aligned} &f(0)=e^{-1}, \quad F(0)=f(0), \quad \pi(0)=\mathbb{E}(S)=\lambda\mu_1=\frac32. \end{aligned} \]

由递推公式可以得出 \(F(x)\) 和 \(\pi(d)\) 的值。

三、案例

正态分布的停止损失保费：设 \(S\sim N(\mu,\sigma^2)\) ，考虑 \(S\) 的取自留额 \(d\) 的停止损失保费。

如果 \(Z\sim N(0,1)\) ，则 \(S\xlongequal{d}\sigma Z+\mu\sim N(\mu,\sigma^2)\) ，于是所要计算的停止损失保费为

\[\mathbb{E}\left[(S-d)_+\right]=\mathbb{E}\left[(\sigma Z+\mu-d)_+\right]=\sigma\left[\mathbb{E}\left(Z-\frac{d-\mu}{\sigma}\right)_+\right]. \]

因此，先考虑特殊情形 \(\mu=0\) 和 \(\sigma^2=1\) ，即标准正态分布情形。

因为 \(\phi'(u)=-u\phi(u)\) ，所以有

\[\int_t^\infty u\phi(u)\mathrm{d}u=\int_t^\infty\left[-\phi'(u)\right]\mathrm{d}u=\phi(t). \]

于是可以得到

\[\pi(t)=\mathbb{E}\left[(Z-t)_{+}\right]=\int_t^\infty(u-t)\phi(u)\mathrm{d}u=\phi(t)-t[1-\Phi(t)], \]

从而有

\[\mathbb{E}\left[(S-t)_{+}\right]=\sigma\phi\left(\frac{d-\mu}{\sigma}\right)-(d-u)\left[1-\Phi\left(\frac{d-\mu}{\sigma}\right)\right]. \]

伽马分布的停止损失保费：设 \(S\sim \Gamma(\alpha,\beta)\) ，用 \(G(x;\alpha,\beta)\) 表示 \(S\) 的分布函数。考虑 \(S\) 的取自留额 \(d\) 的停止损失保费。记 \(\bar{G}(x;\alpha,\beta)=1-G(x;\alpha,\beta)\) 为 \(\Gamma(\alpha,\beta)\) 的生存函数。\

\[\begin{aligned} \mathbb{E}\left[(S-d)_+\right]&=\int_d^\infty(x-d)f(x)\mathrm{d}x \\ \\ &=\int_d^\infty(x-d)\frac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x}\mathrm{d}x\\ \\ &=\int_d^\infty\frac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha}e^{-\beta x}\mathrm{d}x-d\bar{G}(d;\alpha,\beta)\\ \\ &=\frac\alpha\beta\bar{G}(d;\alpha+1,\beta)-d\bar{G}(d;\alpha,\beta) \\ \\ &=\frac\alpha\beta\left[1-G(d;\alpha+1,\beta)\right]-d\left[1-G(d;\alpha,\beta)\right]. \end{aligned} \]

停止损失保费的 NP 近似：对于某些随机变量 \(X\) ，当 \(y>1\) 时，随机事件 \(\{X>y\}\) 的概率用 NP 近似效果较好。考虑对 \(X\) 的停止损失保费，即 \(\mathbb{E}\left[(X-d)_+\right]\) 的给出 NP 近似。

对 \(u\geq1\) 和 \(y\geq1\) ，定义辅助函数：

\[q(u)=u+\frac\gamma6\left(u^2-1\right),\quad w(y)=\sqrt{\frac9{\gamma^2}+\frac{6y}\gamma+1}-\frac3\gamma, \]

易知 \(w(q(u))=u\) 和 \(q(w(y))=y\) ，进一步可知 \(q(\cdot)\) 和 \(w(\cdot)\) 都是单调递增函数，并且

\[q(u)\geq y \quad \iff \quad w(y)\leq u. \]

例如：设 \(Z\) 是一个均值为 \(0\) ，标准差为 \(1\) ，偏度为 \(\gamma>0\) 的随机变量，采用 NP 近似来计算停止损失保费。

由 NP 近似可知

\[\mathrm{Pr}(Z>q(u))=\mathrm{Pr}(w(Z)>u)\approx 1-\Phi(u),\quad u\geq1. \]

设 \(U\sim N(0,1)\) ，定义随机变量 \(V=\max\{q(U),1\}\) 。

由于 \(q(1)=1\) 且 \(q(\cdot)\) 单调，因此当 \(U\geq1\) 时，有 \(q(U)\geq1\) ，所以

\[\mathrm{Pr}(V>q(u))=\mathrm{Pr}(U>u)=1-\Phi(u),\quad u\geq1. \]

由此可得

\[\mathrm{Pr}(Z>q(u))\approx 1-\Phi(u)=\mathrm{Pr}(V>q(u)),\quad u\geq1. \]

当 \(d\geq1\) 时，停止损失保费可以通过 \(V\) 的停止损失保费来近似，即

\[\begin{aligned} \mathbb{E}\left[(Z-d)_+\right]&=\int_d^\infty\mathrm{Pr}(Z>y)\mathrm{d}y \\ \\ &\approx\int_d^\infty\mathrm{Pr}(V>y)\mathrm{d}y=\mathbb{E}\left[(V-d)_+\right] \\ \\ &=\int_{-\infty}^\infty\left(\max\{q(u),1\}-d\right)_+\phi(u)\mathrm{d}u \\ \\ &=\int_{w(d)}^\infty(q(u)-d)\phi(u)\mathrm{d}u. \end{aligned} \]

最后一个等式用到了 \(q(u)\geq y \ \ \iff \ \ w(y)\leq u\) 。

为了计算上面的积分，需要利用如下的结果：

\[\phi'(u)=-u\phi(u), \\ \\ \frac{\mathrm{d}}{\mathrm{d}u}[u\phi(u)]=(1-u^2)\phi(u) \quad \Longrightarrow \quad \int_t^\infty[u^2-1]\phi(u)\mathrm{d}u=t\phi(t). \]

由此可得

\[\begin{aligned} \mathbb{E}\left[(Z-d)_+\right]&\approx \int_{w(d)}^\infty(q(u)-d)\phi(u)\mathrm{d}u \\ \\ &= \int_{w(d)}^\infty\left[u+\frac\gamma6(u^2-1)-d\right]\phi(u)\mathrm{d}u \\ \\ &=\phi(w(d))+\frac\gamma6w(d)\phi(w(d))-d[1-\Phi(w(d))]. \end{aligned} \]

这个公式可用于任何一个满足期望为 \(0\) ，方差为 \(1\) ，偏度为 \(\gamma>0\) 的风险变量 \(Z\) 的停止损失保费的近似公式。