编程题：最长回文子串

最长回文子串

对于一个字符串，请设计一个高效算法，计算其中最长回文子串的长度。

给定字符串A以及它的长度n，请返回最长回文子串的长度。

考察点：字符串、动态规划

思路1：遍历并往前往后查找以该节点i为中心节点回文子串

1、涉及字符串中单个字符的操作，将字符串转成字符数组进行操作

2、回文子串中心节点的格式可能是bab或者baab，根据这个进行一一遍历

    /*返回最长回文子串的长度*/
    /*
    1、字符串若是涉及单字符操作，转换成char数组处理效率更高
    2、方法一：通过交接点寻找,使用stack?
    */
    public int getLongestPalindrome(String A, int n) {
        /*找回文子串的交接点*/
        char[] chara = A.toCharArray();
        int max = 0;
        if(chara[1]==chara[0]) max=2;
        for(int i=2;i<n;i++){
            if(chara[i]==chara[i-1]){
                int l=i-1,r=i;
                while (l>=0&&r<n&&chara[l]==chara[r]){
                    l--;
                    r++;
                }
                max = Math.max(max,r-l-1);
            }
            if(chara[i]==chara[i-2]){
                int l=i-2,r=i;
                while (l>=0&&r<n&&chara[l]==chara[r]){
                    l--;
                    r++;
                }
                max = Math.max(max,r-l-1);

            }

        }
        return max;
    }

思路2：动态规划

一开始并不想构建动态规划，后面了解了一下，不知道构建动态规划矩阵是否对提升效率有帮助？

若是构建动态规划矩阵，设置布尔矩阵dp[i][j] = 位置i到位置j的字符串是否回文子串，那么在判断str[i]和str[j]是否相等的前提，dp[i][j]是否为true与dp[i-1][j+1] 来判断。

这个动态规划矩阵我们只关注左下角部分，可以发现黄色对角线都是true，

而蓝色的位置，譬如A与它的右上角对角位置T‘相关，然而T’在我们关注的三角之外，所以可以默认为true只看A对应位置的两个字符对比。

红色的位置B与它右上角对角位置相关，是为true的黄色位置

紫色位置C与A‘相关，那么我们需要构建矩阵的顺序是从上到下，从右到左。

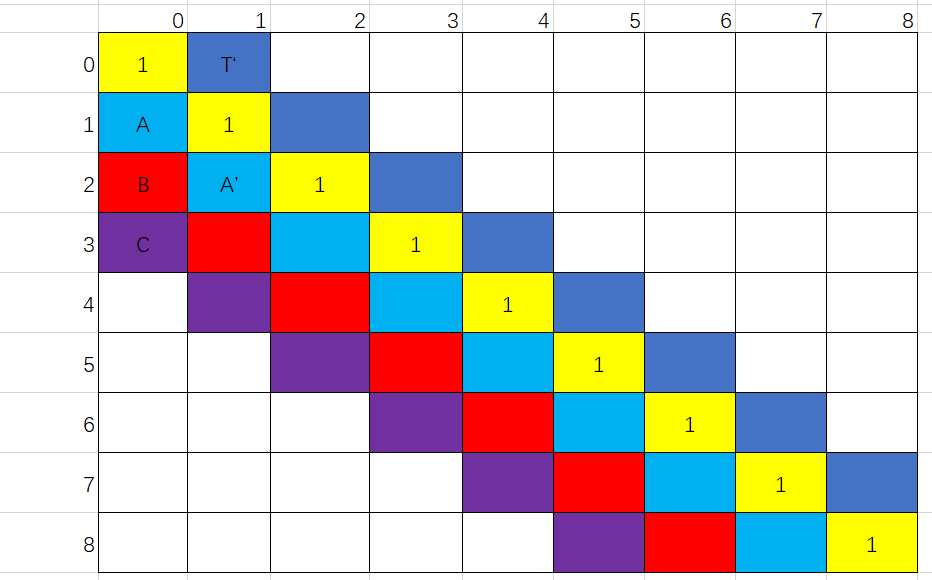
如ccbcabaabba的回文子串矩阵如下

 

 

 

 

解题2：

排名前列的大佬们证明，好像动态规划解法对这道题反而不是最优算法

if (A == null || A.length() < 2 || n < 2) return 1;
        int max = 1;
        boolean[][] dp = new boolean[n][n];
        char[] chara = A.toCharArray();
        for(int i=0;i<n;i++){
            for(int j=i;j>=0;j--){
                if(i==j){ dp[i][j]=true;}
                else if(j+1>i-1){
                   dp[i][j] = (chara[i]==chara[j]);
                }
                else {
                    dp[i][j] = dp[i-1][j+1]&&(chara[i]==chara[j]);
                }

                if(dp[i][j]){
                    //System.out.println(i+" "+j);
                    max = Math.max(max,i-j+1);
                }

            }
        }
        return max;