第04次作业-树

 

1.学习总结

1.1树结构思维导图

 

 

1.2 树结构学习体会

。1.遍历二叉树 是指以一定的次序访问二叉树中的每个结点。所谓 访问结点 是指对结点进行各种操作的简称。例如，查询结点数据域的内容，或输出它的值，或找出结点位置，或是执行对结点的其他操作。

2.对于一个二叉树的存储，首先想到的是能不能用一个数组顺序表存储，用数组下标映射每个节点的存储位置。事实是是可行的，但是存在着诸多问题。
对于完全二叉树是完全可行的，但是对于一般二叉树，就会出现空间浪费的问题。

2.PTA实验作业

 

---

2.1 题目1：

7-7 修理牧场（25 分）

农夫要修理牧场的一段栅栏，他测量了栅栏，发现需要N块木头，每块木头长度为整数L​i​​个长度单位，于是他购买了一条很长的、能锯成N块的木头，即该木头的长度是L​i​​的总和。

但是农夫自己没有锯子，请人锯木的酬金跟这段木头的长度成正比。为简单起见，不妨就设酬金等于所锯木头的长度。例如，要将长度为20的木头锯成长度为8、7和5的三段，第一次锯木头花费20，将木头锯成12和8；第二次锯木头花费12，将长度为12的木头锯成7和5，总花费为32。如果第一次将木头锯成15和5，则第二次锯木头花费15，总花费为35（大于32）。

请编写程序帮助农夫计算将木头锯成N块的最少花费。

2.2 设计思路

 

 

 

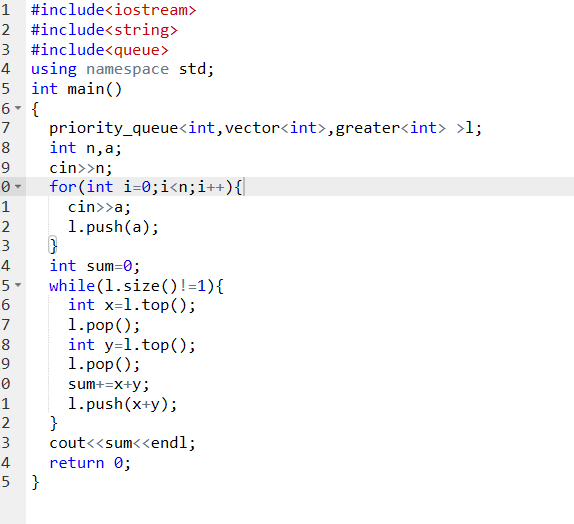
2.3 代码截图

 

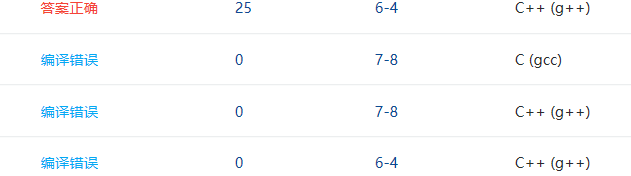
2.4 PTA提交列表说明。

一开始根本不会，搞懂思路后就比较简单了，代码也不算复杂

---

6-4 jmu-ds-表达式树（25 分）

• 输入一行中缀表达式，转换一颗二叉表达式树，并求解.
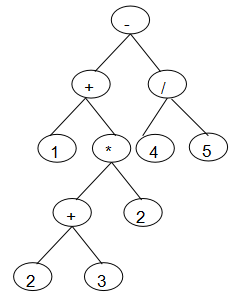
• 表达式只包含+，-，*，/，（，）运算符，操作数只有一位，且为整数(有兴趣同学可以考虑负数小数，两位数做法)。按照先括号，再乘除，后加减的规则构造二叉树。
• 如图所示是"1+(2+3)*2-4/5"代数表达式对应二叉树，用对应的二叉树计算表达式的值。 转换二叉树如下：

6-1 jmu-ds-二叉树操作集（20 分）

本题要求用层次法创建二叉树，层次法输入序列是按树的从上到下从左到右的顺序形成，各层的空节点用字符 #表示，如：

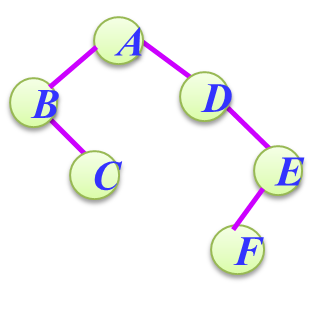
这颗树对应的层次字符串序列为ABD#C#E##F###,即结点的空孩子用#表示。

2.2 设计思路 

 

 

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

 

 

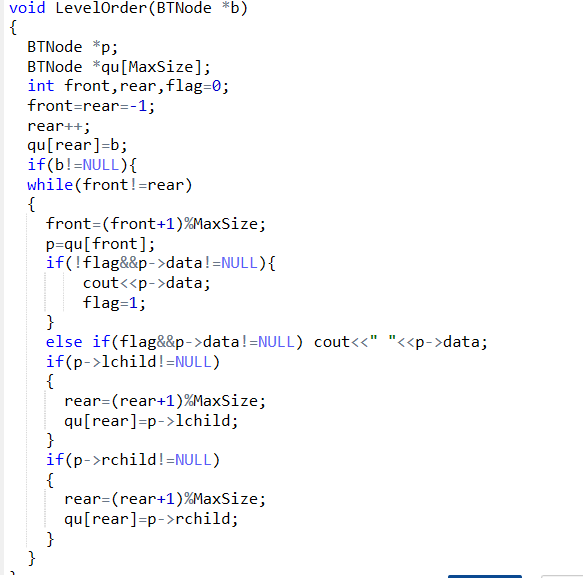
2.4 PTA提交列表说明。

这道题目一直没能搞懂，上完课之后才打出来，对于编译方面的头文件也搞错了

3.截图本周题目集的PTA最后排

3.1 PTA排名截图

 

3.2 我的总分：

本题评分规则：

 2.5

4. 阅读代码（必做）

本次为必做

找1篇和树结构有关的代码，说明该代码功能是什么，优点是什么？

链接：https://www.nowcoder.com/questionTerminal/6e196c44c7004d15b1610b9afca8bd88
来源：牛客网

public class Solution {
    public static boolean HasSubtree(TreeNode root1, TreeNode root2) {
        boolean result = false;
        //当Tree1和Tree2都不为零的时候，才进行比较。否则直接返回false
        if (root2 != null && root1 != null) {
            //如果找到了对应Tree2的根节点的点
            if(root1.val == root2.val){
                //以这个根节点为为起点判断是否包含Tree2
                result = doesTree1HaveTree2(root1,root2);
            }
            //如果找不到，那么就再去root的左儿子当作起点，去判断时候包含Tree2
            if (!result) {
                result = HasSubtree(root1.left,root2);
            }
            
            //如果还找不到，那么就再去root的右儿子当作起点，去判断时候包含Tree2
            if (!result) {
                result = HasSubtree(root1.right,root2);
               }
            }
            //返回结果
        return result;
    }
 
    public static boolean doesTree1HaveTree2(TreeNode node1, TreeNode node2) {
        //如果Tree2已经遍历完了都能对应的上，返回true
        if (node2 == null) {
            return true;
        }
        //如果Tree2还没有遍历完，Tree1却遍历完了。返回false
        if (node1 == null) {
            return false;
        }
        //如果其中有一个点没有对应上，返回false
        if (node1.val != node2.val) { 
                return false;
        }
        
        //如果根节点对应的上，那么就分别去子节点里面匹配
        return doesTree1HaveTree2(node1.left,node2.left) && doesTree1HaveTree2(node1.right,node2.right);
    }

• 给出代码相关
• 重新认识了递归的用法

5. 代码Git提交记录截图