图像旋转原理python实现
最近在学习图像的知识，使用到了图像旋转，所以自己学了一下图像旋转的原理，自己用python写了一遍。
这里用到的知识有图像旋转和双线性插值法，这两篇是我参考的文章：图像旋转算法原理、图像处理之双线性插值法。
简单介绍一下图像旋转的过程：1.首先将图像坐标系转换为数学坐标系。2.使用旋转公式对坐标进行旋转。3.将旋转后的数学坐标系转换为图像坐标系。
其中x，y是转换后的坐标，x0，y0是原始的坐标，θ是旋转的角度；第一个矩阵是将图像坐标系转换为数学坐标系，W和H分别为图像的宽高；第二个矩阵为旋转公式；第三个公式是将数学坐标系转换为图像坐标系，W’和H'分别是新图像的宽高。这里的转换应该是使用了齐次坐标，至于为什么，我也不是很理解。
得到坐标的转换公式如下（公式一）。
通过公式一，就可以从原始的图像坐标获得转换之后的图像坐标。
而另一个图像转换的过程是通过转换后的坐标获得原始图像的坐标，图像旋转的过程：1.将图像坐标转换为数学坐标。2.使用图像旋转的逆公式。3.将数学坐标转换为图像坐标。
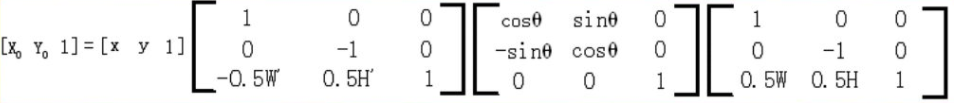
这个和上面的公式对比一下，就是第一个矩阵将W和H换成了W‘和H'；上面那条公式第二个矩阵其实是顺时针旋转的，而这里的是逆时针旋转的；第三条公式将W’和H'换成了W和H。
得到坐标的转换公式如下。（公式二）
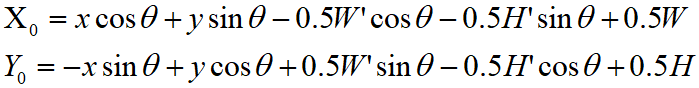
这里就可以通过转换后的图像坐标获得对应的原始图像的坐标。
有了公式，那只要解出未知数的值就可以套用了，其实主要还是求新图像的宽高，因为图像旋转之后，需要一个更大的新图像来装原图像。
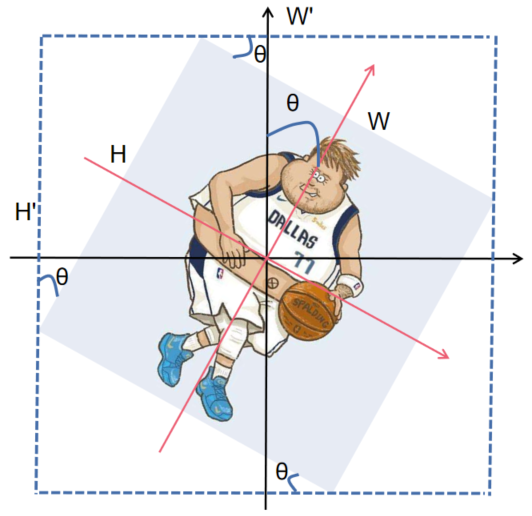
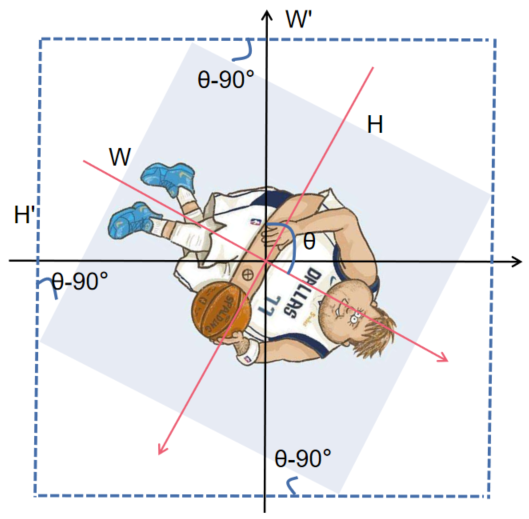
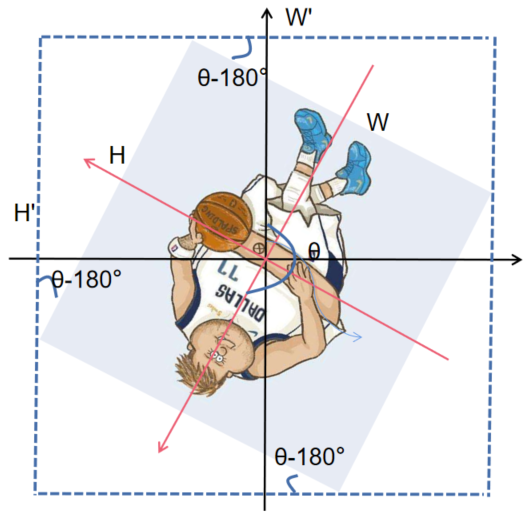
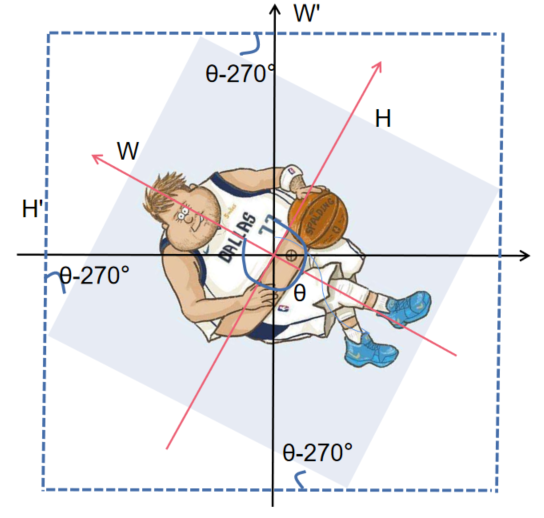
旋转的主要情况分为上面4种情况，旋转了[0，90°)，[90°，180°)，[180°，270°)，[270°，360°)，黑色坐标轴为原始图像坐标轴，红色为旋转后的图像坐标轴。注意图二和图四的宽高相对于图一和图三的宽高是变了位置的。（ps：图片是我最喜欢的球员，东契奇）
以第一张图为例，新图像的长和宽计算公式是
。四个角度相当于θ-0×90°，θ-1×90°，θ-2×90°，θ-3×90°，计算结果可以用θ%90°来得到。但是因为图二和图四的宽高已经变换位置了，为了使用同一条计算新图像宽高的公式，图二图四可以用(90°-(θ%90))得到另一个角的度数，来计算新图像的宽高，只需要计算θ%90°的结果，如果是奇数(1or3)就求另一个角的读书。(想不到其他简便的方法了)
得到新图像的宽高后，就可以写代码了，下面是代码部分。
计算新图像的宽高，因为numpy库里面sin和cos的参数是弧度，所以需要进行角度转弧度。
if int(angle / 90) % 2 == 0: reshape_angle = angle % 90 else: reshape_angle = 90 - (angle % 90) reshape_radian = math.radians(reshape_angle) # 角度转弧度 # 三角函数计算出来的结果会有小数，所以做了向上取整的操作。 new_height = math.ceil(height * np.cos(reshape_radian) + width * np.sin(reshape_radian)) new_width = math.ceil(width * np.cos(reshape_radian) + height * np.sin(reshape_radian))
首先是使用公式一进行前向映射生成新的图像。前向映射就是通过原图像的坐标计算新图像的坐标，再把对应的像素赋值过去。
radian = math.radians(angle) cos_radian = np.cos(radian) sin_radian = np.sin(radian) dx = 0.5 * new_width + 0.5 * height * sin_radian - 0.5 * width * cos_radian dy = 0.5 * new_height - 0.5 * width * sin_radian - 0.5 * height * cos_radian for y0 in range(height): for x0 in range(width): x = x0 * cos_radian - y0 * sin_radian + dx y = x0 * sin_radian + y0 * cos_radian + dy new_img[int(y) - 1, int(x) - 1] = img[int(y0), int(x0)] # 因为整体映射的结果会比偏移一个单位，所以这里x,y做减一操作。
前向映射效果图
可以看到，新图像里面很多像素都没有填充到，因为前向映射算出来的结果有小数，不能一一映射到新图像的每个坐标上。
下面是使用公式二，进行后向映射，后向映射就是通过新图像的每个坐标点找到原始图像中对应的坐标点，再把像素赋值上去。
dx_back = 0.5 * width - 0.5 * new_width * cos_radian - 0.5 * new_height * sin_radian dy_back = 0.5 * height + 0.5 * new_width * sin_radian - 0.5 * new_height * cos_radian for y in range(new_height): for x in range(new_width): x0 = x * cos_radian + y * sin_radian + dx_back y0 = y * cos_radian - x * sin_radian + dy_back if 0 < int(x0) <= width and 0 < int(y0) <= height: # 计算结果是这一范围内的x0，y0才是原始图像的坐标。 new_img[int(y), int(x)] = img[int(y0) - 1, int(x0) - 1] # 因为计算的结果会有偏移，所以这里做减一操作。
后向映射效果图
可以看到使用后向映射，新图像的每个坐标都有像素值。
最后使用填充像素的方法是后向映射+双线性插值法，后向映射得到对应的坐标后，取得坐标最近的四个真实的坐标点，分别乘上不同的权重再求和，就得到了赋值的像素。具体的原理可以看文章开头给的链接。代码如下(channel是图像的通道数，最下面完整的代码会给出声明的地方)。
if channel: fill_height = np.zeros((height, 2, channel), dtype=np.uint8) fill_width = np.zeros((2, width + 2, channel), dtype=np.uint8) else: fill_height = np.zeros((height, 2), dtype=np.uint8) fill_width = np.zeros((2, width + 2), dtype=np.uint8) img_copy = img.copy() # 因为双线性插值需要得到x+1，y+1位置的像素，映射的结果如果在最边缘的话会发生溢出，所以给图像的右边和下面再填充像素。 img_copy = np.concatenate((img_copy, fill_height), axis=1) img_copy = np.concatenate((img_copy, fill_width), axis=0) dx_back = 0.5 * width - 0.5 * new_width * cos_radian - 0.5 * new_height * sin_radian dy_back = 0.5 * height + 0.5 * new_width * sin_radian - 0.5 * new_height * cos_radian for y in range(new_height): for x in range(new_width): x0 = x * cos_radian + y * sin_radian + dx_back y0 = y * cos_radian - x * sin_radian + dy_back x_low, y_low = int(x0), int(y0) x_up, y_up = x_low + 1, y_low + 1 u, v = math.modf(x0)[0], math.modf(y0)[0] # 求x0和y0的小数部分 x1, y1 = x_low, y_low x2, y2 = x_up, y_low x3, y3 = x_low, y_up x4, y4 = x_up, y_up if 0 < int(x0) <= width and 0 < int(y0) <= height: pixel = (1 - u) * (1 - v) * img_copy[y1, x1] + (1 - u) * v * img_copy[y2, x2] + u * (1 - v) * img_copy[y3, x3] + u * v * img_copy[y4, x4] # 双线性插值法，求像素值。 new_img[int(y), int(x)] = pixel
双向性插值法效果图
双向性插值法效果个人感觉没有单独使用后向映射的效果好，不知道是不是我的代码有问题，如果有写法不对的话，可以指出，我再好好学习学习。
总结，这里只实现了顺时针旋转的效果，而逆时针旋转的话，只需要将公式一和公式二中间的旋转公式对换就可以了。另外这里也只是以图像中心点为坐标原点进行旋转的，围绕任意坐标点进行旋转的方法还没吃透，希望有大神可以指点一下。然后这里的代码都是没有经过优化的，只是简单实现效果而已，所以运行速度会比较慢。下面附上完整的代码。
import cv2 import math import numpy as np path = r'E:\pic\p77.jpg' img = cv2.imread(path) height, width = img.shape[:2] if img.ndim == 3: channel = 3 else: channel = None angle = 30 if int(angle / 90) % 2 == 0: reshape_angle = angle % 90 else: reshape_angle = 90 - (angle % 90) reshape_radian = math.radians(reshape_angle) # 角度转弧度 # 三角函数计算出来的结果会有小数，所以做了向上取整的操作。 new_height = math.ceil(height * np.cos(reshape_radian) + width * np.sin(reshape_radian)) new_width = math.ceil(width * np.cos(reshape_radian) + height * np.sin(reshape_radian)) if channel: new_img = np.zeros((new_height, new_width, channel), dtype=np.uint8) else: new_img = np.zeros((new_height, new_width), dtype=np.uint8) radian = math.radians(angle) cos_radian = np.cos(radian) sin_radian = np.sin(radian) dx = 0.5 * new_width + 0.5 * height * sin_radian - 0.5 * width * cos_radian dy = 0.5 * new_height - 0.5 * width * sin_radian - 0.5 * height * cos_radian # ---------------前向映射-------------------- # for y0 in range(height): # for x0 in range(width): # x = x0 * cos_radian - y0 * sin_radian + dx # y = x0 * sin_radian + y0 * cos_radian + dy # new_img[int(y) - 1, int(x) - 1] = img[int(y0), int(x0)] # 因为整体映射的结果会比偏移一个单位，所以这里x,y做减一操作。 # ---------------后向映射-------------------- dx_back = 0.5 * width - 0.5 * new_width * cos_radian - 0.5 * new_height * sin_radian dy_back = 0.5 * height + 0.5 * new_width * sin_radian - 0.5 * new_height * cos_radian # for y in range(new_height): # for x in range(new_width): # x0 = x * cos_radian + y * sin_radian + dx_back # y0 = y * cos_radian - x * sin_radian + dy_back # if 0 < int(x0) <= width and 0 < int(y0) <= height: # 计算结果是这一范围内的x0，y0才是原始图像的坐标。 # new_img[int(y), int(x)] = img[int(y0) - 1, int(x0) - 1] # 因为计算的结果会有偏移，所以这里做减一操作。 # ---------------双线性插值-------------------- if channel: fill_height = np.zeros((height, 2, channel), dtype=np.uint8) fill_width = np.zeros((2, width + 2, channel), dtype=np.uint8) else: fill_height = np.zeros((height, 2), dtype=np.uint8) fill_width = np.zeros((2, width + 2), dtype=np.uint8) img_copy = img.copy() # 因为双线性插值需要得到x+1，y+1位置的像素，映射的结果如果在最边缘的话会发生溢出，所以给图像的右边和下面再填充像素。 img_copy = np.concatenate((img_copy, fill_height), axis=1) img_copy = np.concatenate((img_copy, fill_width), axis=0) for y in range(new_height): for x in range(new_width): x0 = x * cos_radian + y * sin_radian + dx_back y0 = y * cos_radian - x * sin_radian + dy_back x_low, y_low = int(x0), int(y0) x_up, y_up = x_low + 1, y_low + 1 u, v = math.modf(x0)[0], math.modf(y0)[0] # 求x0和y0的小数部分 x1, y1 = x_low, y_low x2, y2 = x_up, y_low x3, y3 = x_low, y_up x4, y4 = x_up, y_up if 0 < int(x0) <= width and 0 < int(y0) <= height: pixel = (1 - u) * (1 - v) * img_copy[y1, x1] + (1 - u) * v * img_copy[y2, x2] + u * (1 - v) * img_copy[y3, x3] + u * v * img_copy[y4, x4] # 双线性插值法，求像素值。 new_img[int(y), int(x)] = pixel cv2.imshow('res', new_img) cv2.waitKey() cv2.destroyAllWindows()
