数据结构与算法（十）---跳表的实现

一、概述

• 什么是跳表
• 跳表怎么实现

二、跳表

1. 跳表的定义和实现意义

• 我们知道二分查找法的前提是有序数组，那么有没有类似的让链表也证婚词类似"二分"查找的算法，那就是跳表了：它支持快速的插入、删除、查找操作，实现方式没有红黑树那么复杂，甚至可以代替它。Redis的有序集合就是使用跳表实现的，

• 链表的随机访问数据的时间复杂度是O(n)，我们在链表的基础上，每两个结点提取一个结点到上一级，我们把抽出来的那一级叫作索引或索引层。图中的 down 表示 down 指针，指向下一级结点。
  
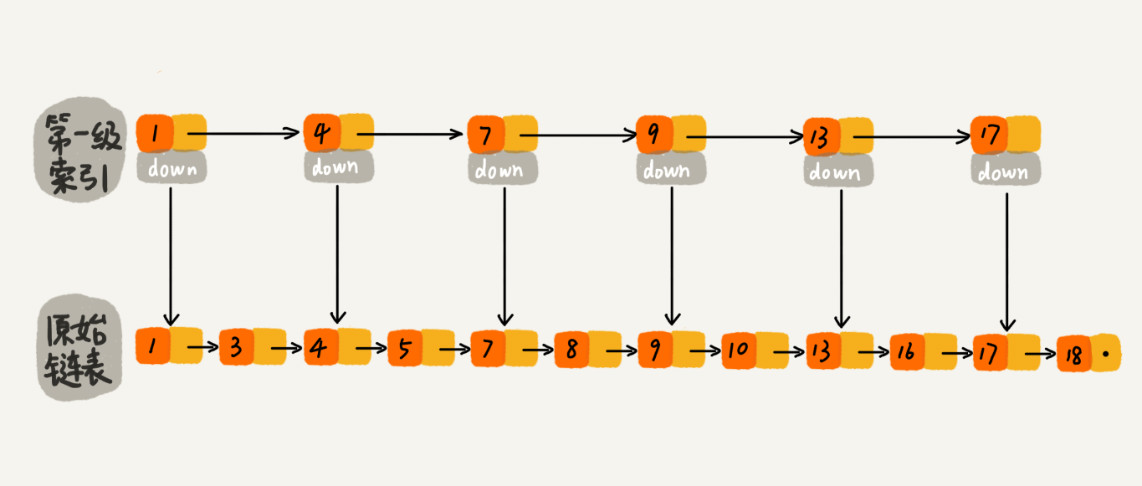
  假如我们要差早16这个元素，我们通过第一级索引进行遍历，当到达13是，发现下一索引元素的值为17，那么16就应该在13和17之间，然后从索引层的13利用down指针，查找到原始链表的13，开始往后遍历得到需要查找的元素，原来需要对遍历10个，现在只需要6个节点；效率提高了；**如果在第一级索引上，在提取一层索引，会怎样呢？

  这里直接查找1-64个元素，体验下效率：
  
  查找效率从62次到了11次，这就是跳表。

2. 跳表的时间复杂度

• 普通链表的时间复杂度是O(N)，怎么计算跳表的时间复杂度呢？

  每两个结点会抽出一个结点作为上一级索引的结点，那第一级索引的结点个数大约就是 n/2，第二级索引的结点个数大约就是 n/4，第三级索引的结点个数大约就是 n/8，依次类推，也就是说，第 k 级索引的结点个数是第 k-1 级索引的结点个数的 1/2，那第 k级索引结点的个数就是 n/(2^k);

  假设索引有h级，最高的索引有两个节点，通过上面的分析，n/(2^h)=2, h=log2n-1,

  如果包含原始链表这一层，整个跳表的高度就是 log2n。我们在跳表中查询某个数据的时候，如果每一层都要遍历 m 个结点，那在跳表中查询一个数据的时间复杂度就是 O(m*logn)。

  那这个 m 的值是多少呢？按照前面这种索引结构，我们每一级索引都最多只需要遍历 3 个结点，也就是说 m=3，为什么是 3 呢？我来解释一下。

  假设我们要查找的数据是 x，在第 k 级索引中，我们遍历到 y 结点之后，发现 x 大于 y，小于后面的结点 z，所以我们通过 y 的 down 指针，从第 k 级索引下降到第 k-1 级索引。在第 k-1 级索引中，y 和 z 之间只有 3 个结点（包含 y 和 z），所以，我们在 K-1 级索引中最多只需要遍历 3 个结点，依次类推，每一级索引都最多只需要遍历 3 个结点。

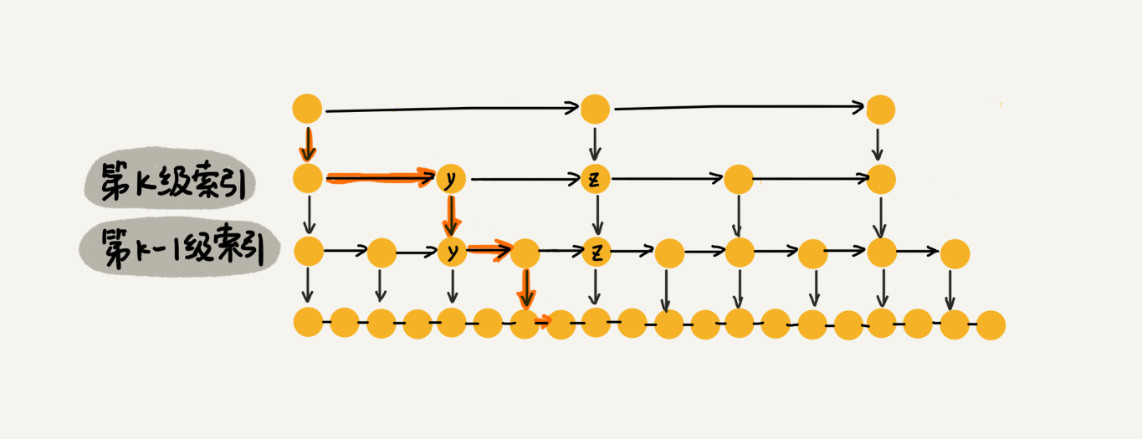
所以跳表查询任意数据的时间复杂度就是O(logn)，和二分查找的时间复杂度是一样的，即基于链表的二分查找法；

3. 跳表的空间复杂度

• 每一级索引，是它下一级索引元素个数的一半，他们的复合等比数列的：

建立一个链表的索引，大概需要n/2+n/4+n/8…+8+4+2=n-2个额外的空间，即空间复杂度是O(n)，如果我们没三个节点抽取一个索引：总的索引结点大约就是 n/3+n/9+n/27+…+9+3+1=n/2。尽管空间复杂度还是 O(n)，但比上面的每两个结点抽一个结点的索引构建方法，要减少了一半的索引结点存储空间。

实际的使用当中，索引只占数据的关键值和几个指针，并不需要存储对象，所以当对象比索引节点大很多时，不用去考虑索引占用额外空间。

4.高效的动态插入和删除

• 我们知道，在单链表中，一旦定位好要插入的位置，插入结点的时间复杂度是很低的，就是 O(1)。但是，这里为了保证原始链表中数据的有序性，我们需要先找到要插入的位置，这个查找操作就会比较耗时。

• 对于纯粹的单链表，需要遍历每个结点，来找到插入的位置。但是，对于跳表来说，我们讲过查找某个结点的的时间复杂度是 O(logn)，所以这里查找某个数据应该插入的位置，方法也是类似的，时间复杂度也是 O(logn)。下面的图中，你可以很清晰地看到插入的过程。

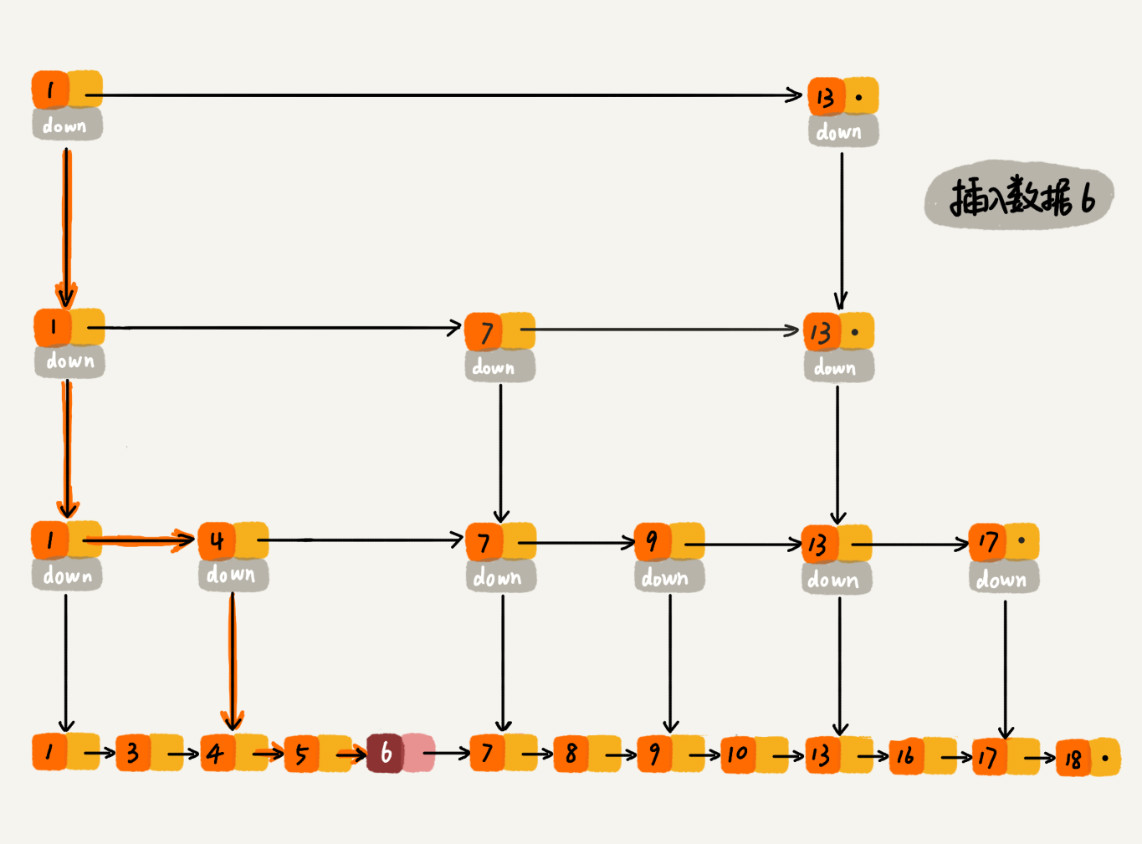
如果这个结点在索引中也有出现，我们除了要删除原始链表中的结点，还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点，然后通过指针操作完成删除。所以在查找要删除的结点的时候，一定要获取前驱结点。当然，如果我们用的是双向链表，就不需要考虑这个问题了。

5.跳表索引动态更新

• 我们不停地往跳表中插入数据时，如果我们不更新索引，就有可能出现某 2 个索引结点之间数据非常多的情况。极端情况下，跳表还会退化成单链表。

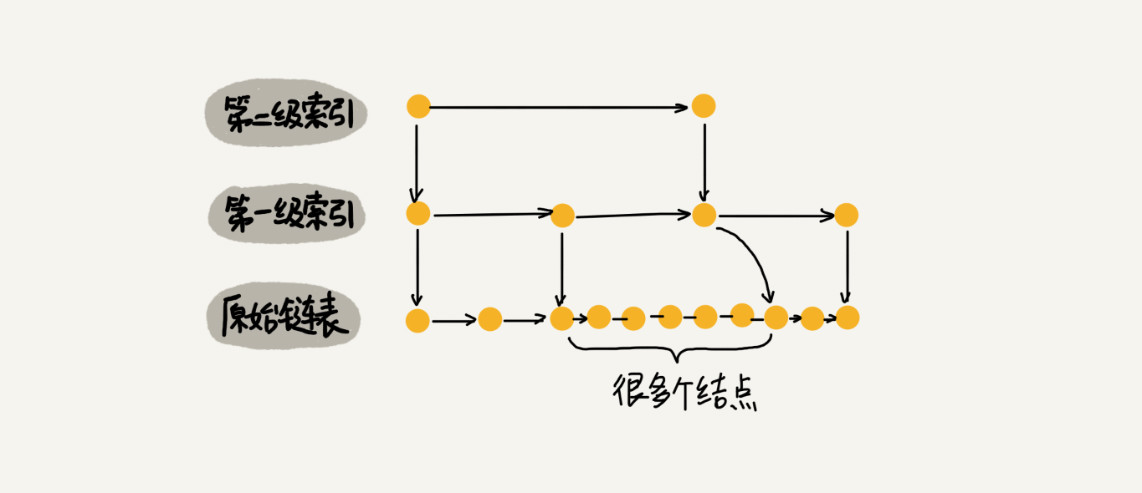
当我们往跳表中插入数据的时候，我们可以选择同时将这个数据插入到部分索引层中。如何选择加入哪些索引层呢？我们通过一个随机函数，来决定将这个结点插入到哪几级索引中，比如随机函数生成了值 K，那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。

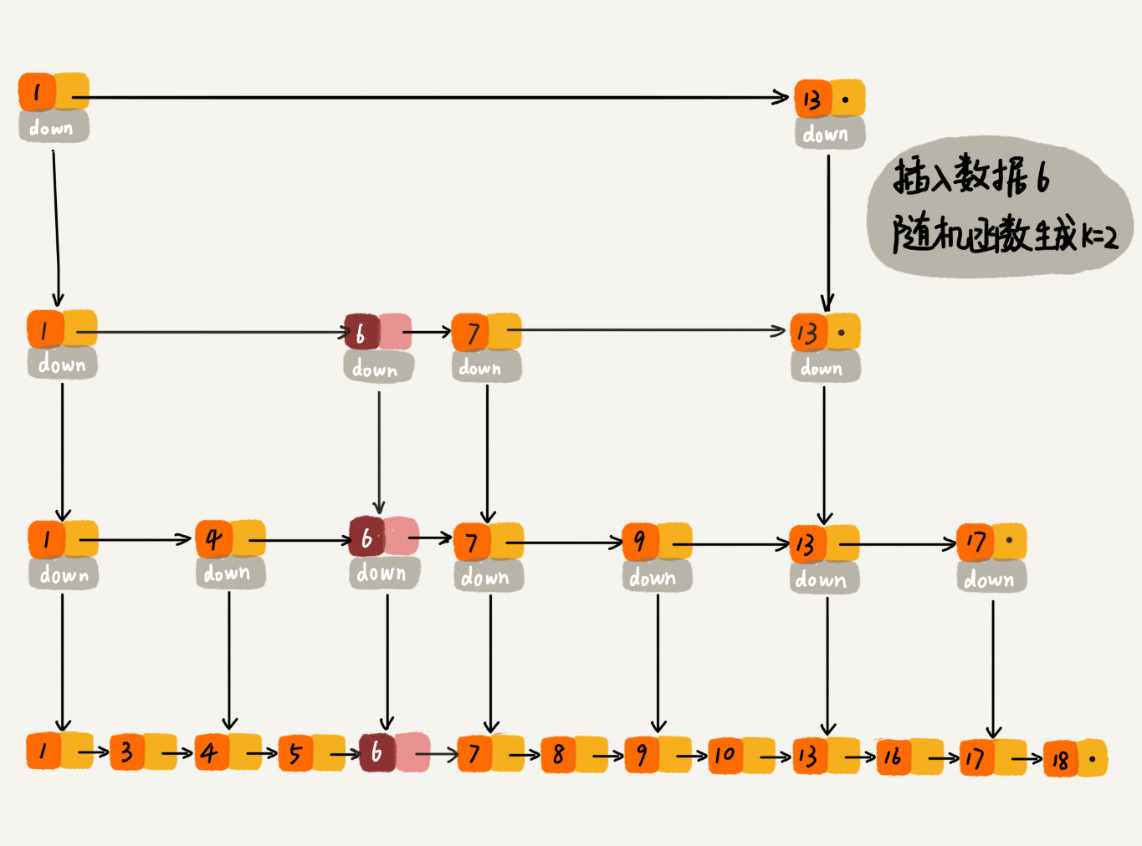
随机函数的选择很有讲究，从概率上来讲，能够保证跳表的索引大小和数据大小平衡性，不至于性能过度退化。

三、开篇问题：为什么 Redis 要用跳表来实现有序集合，而不是红黑树？

Redis 中的有序集合是通过跳表来实现的，严格点讲，其实还用到了散列表。不过散列表我们后面才会讲到，所以我们现在暂且忽略这部分。如果你去查看 Redis 的开发手册，就会发现，Redis 中的有序集合支持的核心操作主要有下面这几个：

• 插入一个数据
• 删除一个数据
• 按照区间查找数据（比如查找值在 [100, 356] 之间的数据）
• 迭代输出有序序列

其中，插入、删除、查找以及迭代输出有序序列这几个操作，红黑树也可以完成，时间复杂度跟跳表是一样的。但是，按照区间来查找数据这个操作，红黑树的效率没有跳表高。

当然，Redis 之所以用跳表来实现有序集合，还有其他原因，比如，跳表更容易代码实现。虽然跳表的实现也不简单，但比起红黑树来说还是好懂、好写多了，而简单就意味着可读性好，不容易出错。还有，跳表更加灵活，它可以通过改变索引构建策略，有效平衡执行效率和内存消耗。

跳表也不能完全替代红黑树。因为红黑树比跳表的出现要早一些，很多编程语言中的 Map 类型都是通过红黑树来实现的。我们做业务开发的时候，直接拿来用就可以了，不用费劲自己去实现一个红黑树，但是跳表并没有一个现成的实现，所以在开发中，如果你想使用跳表，必须要自己实现。

四、课后思考

在今天的内容中，对于跳表的时间复杂度分析，我分析了每两个结点提取一个结点作为索引的时间复杂度。如果每三个或者五个结点提取一个结点作为上级索引，对应的在跳表中查询数据的时间复杂度是多少呢