微积分笔记

前置例题

1.

    S1=1+2+4+8+16+···
   2S1=  2+4+8+16+···
2S1-S1=-1
    S1=-1

2.

  x=0.9999···
10x=9.9999···
 9x=9
  x=1

---

函数的导数和微分

函数的不定积分和定积分

---

知识点1　平均变化率

一般地，已知函数\(y=f\left( x\right)\),\(x_{0},x_{1}\)是定义域内不同的两点，记\(\Delta x=x_{1}-x_{0}\),\(\Delta y=y_{1}-y_{0}=f\left( x_{1}\right) -f\left( x_{0}\right) =f\left( x_{0}+\Delta x\right) -f\left( x_{0}\right)\)。
则当\(\Delta x\neq 0\)时，商\(\dfrac {\Delta y}{\Delta x}=\dfrac {f\left( x_{0}+\Delta x\right) -f\left( x_{0}\right) }{\Delta x}\)称作函数\(y=f\left( x\right)\)在区间\(\left[ x_{0},x_{0}+\Delta x\right]\)或\(\left[ x_{0}+\Delta x,x_{0}\right]\)的平均变化率。

例1

求函数\(y=x^{2}\)在区间\(\left[ x_{0},x_{0}+\Delta x\right]\)的平均变化率。
解：\(\dfrac {\Delta y}{\Delta x}=\dfrac {\left( x_{0}+\Delta x\right) ^{2}-x^{2}_{0}}{\Delta x}=\Delta x+2x_{0}\)

例2

求函数\(y=\dfrac {1}{x}\)在区间\(\left[ x_{0},x_{0}+\Delta x\right]\)的平均变化率。
解：\(\dfrac {\Delta y}{\Delta x}=\dfrac {\dfrac {1}{x_{0}+\Delta x}-\dfrac {1}{x_{0}}}{\Delta x}=-\dfrac {1}{x_{0}\left( x_{0}+\Delta x\right) }\)

知识点2　瞬时变化率

如果\(\Delta x\)趋近于0，平均变化率\(\dfrac {\Delta y}{\Delta x}=\dfrac {f\left( x_{0}+\Delta x\right) -f\left( x_{0}\right) }{\Delta x}\)趋近于常数l，那么称常数l为函数\(y=f\left( x\right)\)在点\(x_{0}\)处的瞬时变化率，记作：
当\(\Delta x\rightarrow 0\)时，\(\dfrac {f\left( x_{0}+\Delta x\right) -f\left( x_{0}\right) }{\Delta x}\rightarrow l\)
也记作$$\lim {\Delta x\rightarrow 0}\dfrac {f\left( x+\Delta x\right) -f\left( x_{0}\right) }{\Delta x}= l$$

知识点3

函数\(y=f\left( x\right)\)在点\(x_{0}\)处的瞬时变化率，通常称为\(f\left( x\right)\)在点\(x_{0}\)处的导数。
记作：\(f'\left( x_{0}\right)\)
即$$\lim {\Delta x\rightarrow 0}\dfrac {f\left( x+\Delta x\right) -f\left( x_{0}\right) }{\Delta x}= f'\left( x_{0}\right)$$

知识点4　导数

如果\(y=f\left( x\right)\)在开区间\(\left( a,b\right)\)内每一点都是可导的，区间\(\left( a,b\right)\)内的每一个值都对应一个确定的导数\(f'\left( x\right)\)，称区间\(\left( a,b\right)\)内\(f'\left( x\right)\)可构成一个新的函数，称为\(y=f\left( x\right)\)的导函数。
记作：\(f'\left( x\right)(\)或$ y'\(或\)y'x)$,通称为导数。

例3

火箭竖直向上发射，熄火时速度达到100m/，试问熄火多长时间，火箭的速度为0。
解：
\(h\left( t\right) =100t-\dfrac {1}{2}gt^{2}\)
平均变化率(平均速度)：\(\dfrac {h\left( t+\Delta t\right) -h\left( t\right) }{\Delta t}=100-\dfrac {1}{2}g\Delta t-gt\)
瞬时速度：\(\Delta t\rightarrow 0\)时
\(\dfrac {h\left( t+\Delta t\right) -h\left( t\right) }{\Delta t}=100-gt\)
令\(100-gt=0,g=9.8\)
\(t=\dfrac {100}{g}\approx10.2s\)

例4

圆，面积\(S=\pi r^{2}\)，周长\(l=2\pi r\)
解：$$S'\left( x\right) =\lim _{\Delta r\rightarrow 0}\dfrac {S\left(r+\Delta r\right) -S\left( r\right) }{\Delta r}$$

\[=\lim _{\Delta r\rightarrow 0}\dfrac {\pi \left( r-\Delta r\right) ^{2}-r^{2}}{\Delta r} \]

\[=\lim _{\Delta r\rightarrow 0}\dfrac {2\pi r\Delta r+\pi \Delta r^{2}}{\Delta r} \]

\[=\lim _{\Delta r\rightarrow 0} {(2\pi r+\pi \Delta r)}=2\pi r \]

知识点5　导数的几何意义

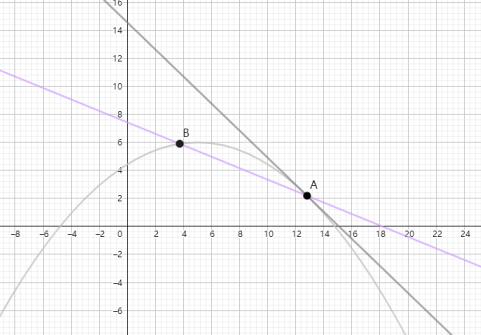
\(A\left( x_{0},f\left( x_{0}\right) \right) , B\left( x_{0}+\Delta x,f\left( x_{0}+\Delta x\right) \right)\)
AB:割线（平均变化率）：\(\dfrac {\Delta y}{\Delta x}=\dfrac {f\left( x_{0}+\Delta x\right) -f\left( x_{0}\right) }{\Delta x}\)
切线（瞬时变化率）：\(\Delta x\rightarrow 0\)，\(\dfrac {\Delta y}{\Delta x}\rightarrow k\)
\(B\rightarrow A\)（转动）
割线\(AB\rightarrow\)切线$ AB’\( 割线斜率\)\rightarrow$切线斜率

\[f\left( x_{0}\right)=k=\lim _{\Delta x\rightarrow 0}\dfrac {f\left( x_{0}+\Delta x\right) -f\left( x_{0}\right) }{\Delta x} \]

函数在一点的切线的斜率就是函数在这点的导数：导数=斜率

例5

求抛物线\(y=x^{2}\)在点\(\left( x_{0},f\left( x_{0}\right) \right)\)切线的斜率。

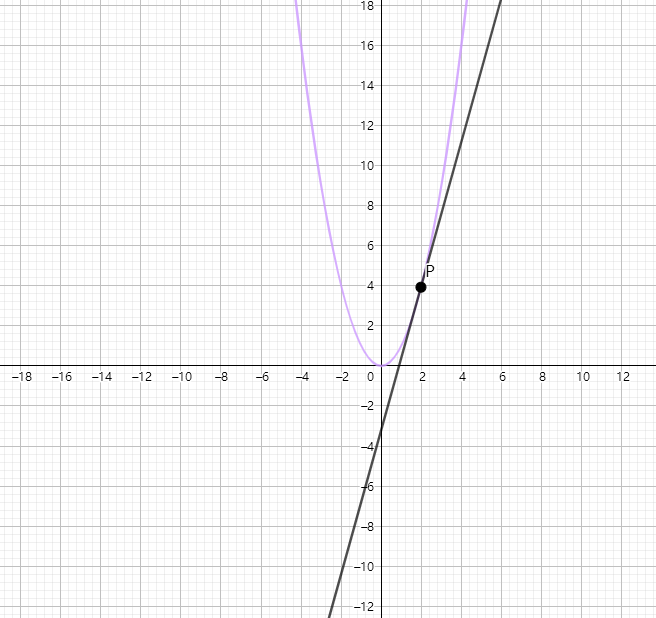
解：求导数的几何意义
知$$k=f\left( x_{0}\right)$$

\[=\lim _{\Delta x\rightarrow 0}\dfrac {f\left( x_{0}+\Delta x\right) -f\left( x_{0}\right) }{\Delta x} \]

\[=\lim _{\Delta x\rightarrow 0}\dfrac {\left( x_{0}+\Delta x\right) ^{2}-x^{2}_{0}}{\Delta x} \]

\[=\lim _{\Delta x\rightarrow 0}(\Delta x+2x_{0}) \]

\[=2x_{0} \]

求在（0,0）处切线的斜率

\[f\left( x\right)=k=0 \]

例6

求双曲线\(y=\dfrac {1}{x}\)在点
\(\left( 2,\dfrac {1}{2}\right)\)的切线方程
方程\(y-y_{0}=k\left( x-x_{0}\right)\)
\(k=-\dfrac {1}{x^{2}}=-\dfrac {1}{4}\)
\(y=-\dfrac {1}{4}x+1\)

知识点6　导数的运算

(1)常值函数的导数
\(y=f\left( x\right) =c\)(c为常数)

\[y'=f'\left( x\right) =c'=\lim _{\Delta x\rightarrow 0}\dfrac {f\left( x_{0}+\Delta x\right) -f\left( x_{0}\right) }{\Delta x} \]

\[=\lim _{\Delta x\rightarrow 0} \dfrac {c-c}{\Delta x}=0 \]

(2)
\(y=x\\ y'=x'=1\)
(3)
\(y=x^{2}\\ y'=\left( x^2\right) '=2x\)
(4)
\(y=x^{3}\\ y'=3x^{2}\)
(5)
\(y=\dfrac {1}{x}\\ y'=-\dfrac {1}{x^{2}}\)
(6)
\(y=\dfrac {1}{\sqrt {x}}\\ y'=\dfrac {1}{2\sqrt {x_{0}}}\)

\[y'=\lim _{\Delta x\rightarrow 0}\dfrac {f\left( x_{0}+\Delta x\right) -f\left( x_{0}\right) }{\Delta x} \]

\[=\lim _{\Delta x\rightarrow 0}\dfrac {\sqrt {x_{0}+\Delta x}-\sqrt {x_{0}}}{\Delta x} $$(分母有理化) $$=\lim _{\Delta x\rightarrow 0}\dfrac {1}{\sqrt {x_{0}+\Delta x}+\sqrt {x_{0}}}=\dfrac {1}{2\sqrt {x_{0}}} \]

知识点7　导数公式表

\(y=f\left( x\right) ,y'=f'\left( x\right)\)
$ y=c,y'=0\( \) y=x^{n}\left( n\in N+\right) ,y'=nx^{n-1}\( \)y=x^{\alpha }( \alpha \in Q,x>0), y'=\alpha x^{\alpha -1}\( \)y= a^{x}(a > 0,a\neq 1),y'=a^{x}\ln a\( \)y=\log a^{x}( a >0,a\neq 1),y'=\dfrac {1}{x\ln a}\( 特别地 \)y=e^{x},y'=e\ y=\ln x,y'=\dfrac {1}{x}\ y=\sin x,y'=\cos x\ y=\cos x,y'=-\sin x\( 补充： \)y=\ln \left| x\right| ,y'=\dfrac {1}{\left| x\right| }\ y=\tan x,y'=\sec ^{2}x=\dfrac {1}{\cos ^{2}x}\( \)y=\arcsin x,y'=\dfrac {1}{\sqrt {1-x^{2}}}\ y=\arccos x,y'=-\dfrac {1}{\sqrt {1-x^{2}}}\( \)y=\arctan x,y'=\dfrac {1}{1+x^{2}}\ y=arccotx,y'=-\dfrac {1}{1+x^{2}}\( 证明\)y=\arcsin x,y'=\dfrac {1}{\sqrt {1-x^{2}}}$:

\[\arcsin x=\theta \\ \Downarrow \\ \sin \theta =x \]

\[\cos\Delta\theta =\Delta x\\ \theta '=\dfrac {\Delta \theta }{\Delta x}=\dfrac {1}{\cos \theta }=\dfrac {1}{\sqrt {1-\sin ^{2}\theta }}\\ \Downarrow \\ \left( \arcsin x\right) '=\dfrac {1}{\sqrt {1-x^{2}}} \]

极限：
“\(\dfrac {0}{0}\)”$$\lim _{x\rightarrow 0}\dfrac {\sin x}{x}=1$$
"\(\dfrac {\infty }{\infty }\)"$$\lim _{x\rightarrow 0}\left( 1+\dfrac {1}{x}\right) ^{x}=e$$
或$$\lim _{x\rightarrow 0}\left( 1+x\right) ^{\dfrac {1}{x}}=e$$

例7

求导
\(f\left( x\right) =x^{5}+2x^{4}+x^{3},g\left( x\right) =3^{x}+\ln x,h\left( x\right) =\cos x+\sin x\)
　　　　　　　　　　　　　　　　\(\Downarrow\)
\(f'\left( x\right) =5x^{4}+8x^{3}+3x^{2},g'\left( x\right) =3^{x}\ln 3+\dfrac {1}{x}, h'\left( x\right) =-\sin x+\cos x\)

知识点8　导数的四则运算

(1)函数和(或差)的求导法则
\(\left[ f\left( x\right) \pm g\left( x\right) \right]'=f'\left( x\right) \pm g'\left( x\right)\)
(2)函数的积的求导法则
\(\left[ f\left( x\right) \cdot g\left( x\right) \right] '=f'\left( x\right) \cdot g\left( x\right) +f\left( x\right) \cdot g'\left( x\right)\)
(3)导数商的求导法则
\(\left[ \dfrac {f\left( x\right) }{g\left( x\right) }\right] ^{'}=\dfrac {f'\left( x\right) g\left( x\right) -f\left( x\right) g'\left( x\right) }{g^{2}\left( x\right) }\)
证明：

\[\left[ \dfrac {f\left( x\right) }{g\left( x\right) }\right] ^{'}=\lim _{\Delta x\rightarrow 0}\dfrac {\dfrac {f\left( x+\Delta x\right) }{g\left( x+\Delta x\right) }-\dfrac {f\left( x\right) }{g\left( x\right) }}{\Delta x} \]

\[=\lim _{\Delta x\rightarrow 0}\dfrac {f\left( x+\Delta x\right) g\left( x\right) -f\left( x\right) g\left( x+\Delta x\right) }{g\left( x+\Delta x\right) g\left( x\right) \Delta x} \]

\[=\dfrac {f'\left( x\right) g\left( x\right) -f\left( x\right) g'\left( x\right) }{g^{2}\left( x\right) } \]

例8

求\(f\left( x\right) =a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+\ldots +a_{n-1}x+a_{n}\)的导数
解：
\(f\left( x\right) =na_{0}x^{n-1}+(n-1)a_{1}x^{n-2}+\ldots +a_{n}-1\)

例9

\(y=x\cdot \sin x\)
解：
\(y'=x'\sin x+x\cdot \left( \sin x\right) '\\ =\sin x+x\cdot \cos x\)

例10

\(y=\sin 2x\)
解：
\(y=\sin 2x=2\sin x\cos x\\ y'=2(\cos ^{2}x-\sin ^{2}x )\\ =2\cos 2x\)

例11

\(y=\tan x=\dfrac {\sin x}{\cos x}\)
解：
\(y'=\dfrac {\left( \sin x\right) '\cos x-\sin x\left( \cos x\right)' }{\cos ^{2}x}\)
\(=\dfrac {\cos ^{2}x+\sin ^{2}x}{\cos ^{2}x}\\ =\dfrac {1}{\cos ^{2}x}\)

知识点9　利用导数判断函数的单调性

(1)如果(a,b)内\(f'\left( x\right) >0\)，函数单调递增
(2)如果(a,b)内\(f'\left( x\right) <0\)，函数单调递减

例13

y=x在\(\left( -\infty ,+\infty \right)\)上的单调性
解：\(y'=1 >0\)

例14

\(y=2x^{2}-2x+4\)在\(\left( -\infty ,+\infty \right)\)上的单调性
解：\(y'=2x-2\)
令\(y' >0\)，即\(x >1\)，在\(\left( 1,+\infty \right)\)上函数单调递增
令\(y' <0\)，即\(x <1\)，在\(\left( -\infty ,1\right)\)上函数单调递减

例15

\(y=x^{3}-4x^{2}+x-1\)
解：
\(y'=3x^{2}-8x+1\)
令\(y' >0\)，即在\(\left( -\infty ,\dfrac {4-\sqrt {13}}{3}\right) ,\left( \dfrac {4+\sqrt {13}}{3},+\infty \right)\)上函数单调递增
令\(y' <0\)，即在\(\left( \dfrac {4-\sqrt {13}}{3} ,\dfrac {4+\sqrt {13}}{3} \right)\)上函数单调递减

知识点10　利用导数研究函数的性质

\(y=\dfrac {1}{3}x^{3}-4x+4\\ y'=x^{2}-4\)
令\(y=0\)即\(x=\pm2\)

x	(\(-\infty\),-2)	-2	(-2,2)	2	(2,\(+\infty\))
\(f'\left( x\right)\)	+		-		+
\(f\left( x\right)\)	\(\nearrow\)	极大值	\(\searrow\)	极小值	\(\nearrow\)

知识点11　曲边梯形与定积分

例16

求曲线\(y=x^{2}\)与直线\(x=1,y=0\)所围成区域的面积。
解：

[0,1]等分。
\(S_{n}=0+\left( \dfrac {1}{n}\right) ^{2}\cdot \dfrac {1}{n}+\left( \dfrac {2}{n}\right) ^{2}\cdot \dfrac {1}{n}+\ldots +\left( \dfrac {n-1}{n}\right) ^{2}\cdot \dfrac {1}{n}=\dfrac {1}{n^{3}}\)
\(\left[ 1^{2}+2^{2}+\ldots +\left( n-1\right) ^{2}\right] =\dfrac {1}{n^{3}}\)
\(\dfrac {n\left( n-1)(2n-1\right) }{6}=\dfrac {1}{6}\left( 1-\dfrac {1}{n}\right) \left( 2-\dfrac {1}{n}\right)\)
\(n\rightarrow \infty\)时

\[\lim _{n\rightarrow \infty }\dfrac {1}{6}\left( 1-\dfrac {1}{n}\right) \left( 2-\dfrac {1}{n}\right)= \dfrac {1}{3} \]

例12

\(y=f\left( u\right) ,u=ax+b\)，求\(\dfrac {\Delta y}{\Delta x}\)
解：\(u'=a\)
\(\dfrac {\Delta y}{\Delta x}=\dfrac {\Delta y}{\Delta u}\cdot \dfrac {\Delta u}{\Delta x}\)
\(=f'\left( u\right) \cdot u'\left( x\right)\)
\(=a\cdot f'\left( u\right)\)

eg1

\(\mu =x^{-1},g\left( x\right) =4x^{2}+3x\)
解：
\(g\left( u\right) =4u^{2}+3u\\ g'\left( u\right) =8u+3\\ u'=-1\cdot x^{-2}=-\dfrac {1}{x^{2}}\)

eg2

\(\left[ \sin \left( 2x+\dfrac {\pi }{3}\right) \right]'\)
解：
\(u=2x+\dfrac {\pi }{3} \\y=\sin u\\ =\cos u\cdot 2\\ =2\cos \left( 2x+\dfrac {\pi }{3}\right)\)

eg3

\(\left[ \left( 5x+3\right) ^{5}\right] '\)
解：
\(y=u,u=5x+3,u'=5\)
\(y'=f'\left( u\right) \cdot u'\left( x\right) \\ =5u^{4}\cdot 5\\ =25\left( 5x+3\right) ^{4}\)

知识点12　[a,b]n分

\(a=x_{0} <x_{1} <x_{2} <\ldots <x_{n}=b\)

\[I\left( n\right) =\sum ^{n-1}_{i=0}f\left( \varepsilon i\right) \Delta xi \]

\(x_{i}=\max\){\(\Delta xi\)}

\[\lambda _{i}\rightarrow 0\\ \lim _{\lambda i\rightarrow 0}f\left( \varepsilon i\right) \Delta xi\rightarrow l$$定积分 记作$$\int ^{b}_{a}f\left( x\right) \Delta x= \lim _{\lambda i\rightarrow 0}\sum ^{n-1}_{i=0}f\left( \varepsilon i\right) \Delta xi\]

\(f\left( x\right)\)：倍积函数

例16（续）

\(S=\int ^{1}_{0}x^{2}\Delta x=\dfrac {1}{3}\)

知识点13　微积分基本定理

如果\(F\left( x\right) '=f\left( x\right)\)且\(f\left( x\right)\)在\([a,b]\)内可积
则
\(\int ^{b}_{a}f\left( x\right) \Delta x\)
$ =F\left( x\right) \int ^{b}_{a}\( \) =F\left( b\right) -F\left( a\right) $

例17

\(\int ^{1}_{0}x^{2}\Delta x=\)
解：
\(\because \left( \dfrac {1}{3}x^{3}\right) '=x^{2}\\ \therefore \int ^{1}_{0}x^{2}\Delta x\\ =\dfrac {x^{3}}{3}\int ^{1}_{0}=\dfrac {1}{3}\)

例18

\(\int ^{2}_{0}\left( x^{2}+1\right) \Delta x\\ =\left( \dfrac {x^{3}}{3}+x\right) \int ^{2}_{0}\)

例19

\(\int ^{\pi }_{0}\sin \Delta x\\ =-\cos x\int ^{\pi }_{0}\)