数据平滑技术(总结)
参考书籍:《统计自然语言处理》 宗成庆
一、问题的提出


平滑技术就是用来解决句子中出现零概率的问题,“平滑”处理的基本思想是“劫富济贫”,即提高低概率(零概率),降低高概率,尽量使概率的分布趋于实际水平。
二、几种数据平滑技术
1.加法平滑技术
是实际应用中最简单的一种平滑技术,上世纪前半叶由Lidstone, Johnson, Jeffreys等人提出和改进。
基本思想:假设每个n元语法发生的次数比实际统计次数多发生δ次,0≤δ≤1。
通用公式: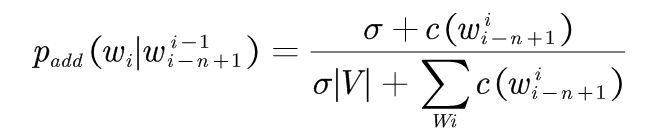 (1-1)
(1-1)
Lidstone和Jeffreys倡议取δ=1,V是所考虑的所有词汇的单词表, |V|为词汇表中单词的个数。 假设V取无穷大,那么分母就是无穷大,所有的概率都趋于0,但现实中,词表中词的个数是几万到几十万个,是有限的。
例如:在二元语法中,假设每个二元语法出现的次数比统计出现的次数多一次,即取δ=1,该处理方法称为:加1平滑
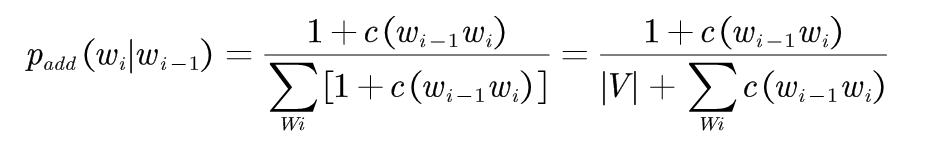 (1-2)
(1-2)
未登录词(未知词): 所有不在词汇表中的词可以映射为一个单个的区别于其他已知词汇的单词。
加法平滑python实现 https://www.cnblogs.com/liweikuan/p/14259886.html
2.古德-图灵(Good-Turing)估计法
Good-Turing估计法是很多平滑技术的核心,1953年由I.J.Good引用图灵(Turing)的方法提出的。
基本思路:对于任何一个出现r次的n元语法,都假设它出现了r*次,用r*代替r。
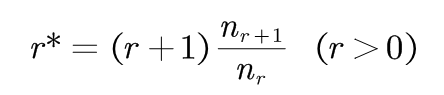 (2-1)
(2-1)
nr是训练语料中统计出现r次的n元语法的数目。 r*对原来的统计次数r进行了折扣,所以r*< r。
要把统计数r*转化为概率值,需要进行归一化处理,即:
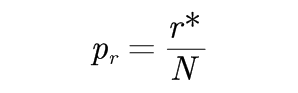 其中,
其中, 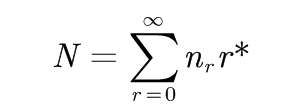
将r*用r替换得到: 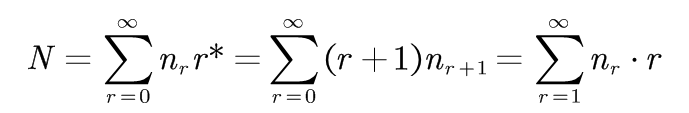
也就是,N等于这个分布中最初的计数。 这样, 样本中所有事件的概率之和为:
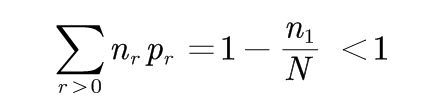 (2-2)
(2-2)
(2-2)式的推导:
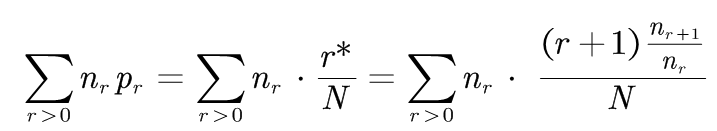
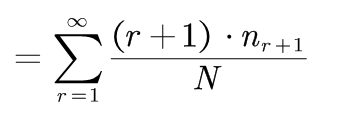
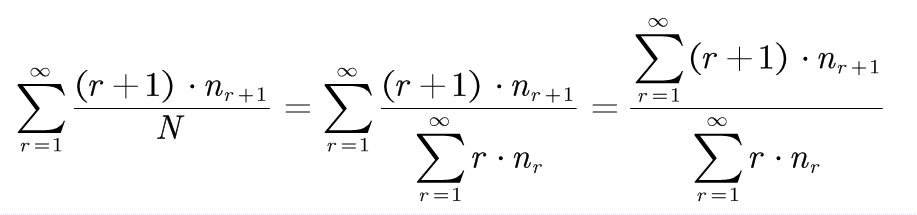
即:
而: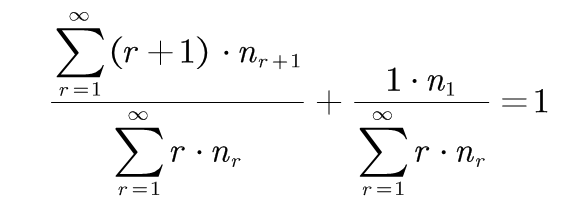 其中
其中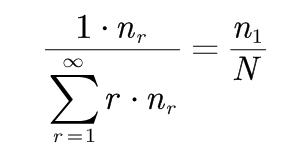
因此:剩余n1/N的概率量可以分配给所有未见的事件(r=0的事件)。
弊端:Good-Turing方法不能实现高阶模型和低阶模型的结合,而高低阶模型的结合通常是获得较好的平滑效果所必须的。
3.Katz平滑方法
1987年S.M.Katz提出一种后备(back-off)平滑方法,简称Katz平滑方法。
基本思路:当事件在样本中出现的频数大于某一数值k时,运用最大似然估计方法,通过减值来估计其概率值;当事件在样本中出现的频数小于k时,使用低阶语法模型作为代替高阶语法模型的后备,这中替换受归一化因子的约束。
实质上:把从高阶模型上减值的概率根据低阶语法模型的分布情况分配给未发生的事件。 这种方法比将剩余概率平均分配给为发生时间更加合理。
以二元语法模型为例说明Katz思想:
对于一个出现次数为![]() 的二元语法
的二元语法![]() ,使用如下公式计算修正的计数:
,使用如下公式计算修正的计数:
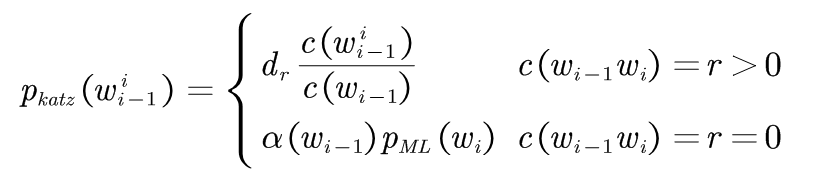 (3-1)
(3-1)
拥有非零计数r的二元语法都根据折扣率dr被减值了,折扣率dr近似等于r*/r, 这个减值是由Good-Turing估计方法预测的。 式中![]() 为
为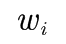 的最大似然估计概率。
的最大似然估计概率。
折扣率dr的计算: 由于大的计数值是可靠的,因此它们不需要减值。 对于r>k的计数,保持原值;对于r≤k情况下的折扣率,由全局二元语法分布的Good-Turing估计方法计算,及(2-1)式中的nr表示在训练语料中恰好出现r次的二元语法的总数。
dr的约束条件:1.最终折扣量与Good-Turing估计预测的减值量成正比例。
2.全局二元语法分布中被折扣的计数总量等于根据Good-Turing估计应该分配给次数为零的二元语法的总数。
第一个约束条件相当于对于某些常数μ,r属于{1,2,.........., k}有公式:
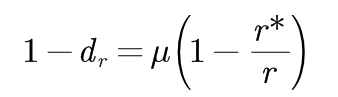 (3-2)
(3-2)
Good-Turing估计方法预测出应该分配给计数为0的二元语法的计数总量为n1,因此第二个约束条件相当于公式:
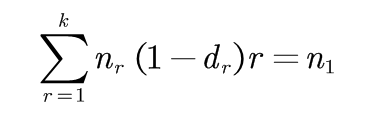 (3-3)
(3-3)
满足(3-2)和(3-3)公式的唯一解为:
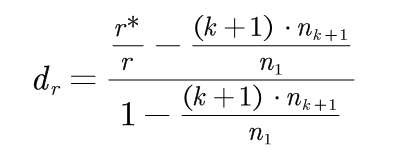 (3-4)
(3-4)
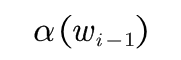 的计算 :
的计算 :
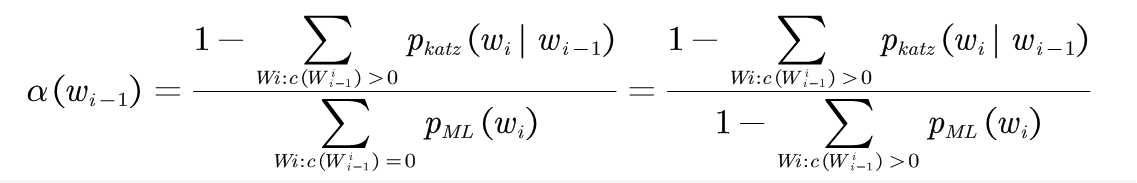 (3-5)
(3-5)
(3-5)式推导:
对于任何一个二元语法模型<Wi-1,Wi>,都应该满足: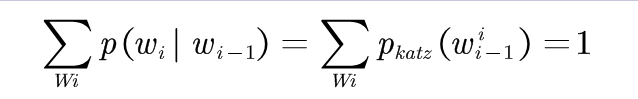 (3-6)
(3-6)
即: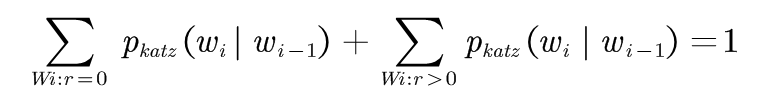 (3-7)
(3-7)
将(3-1)中修正的计数带入(3-7)中得:
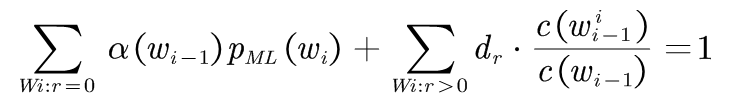 (3-8)
(3-8)
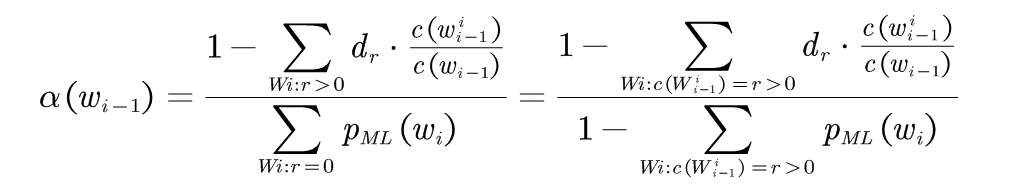 (3-9)
(3-9)
最终根据修正的计数计算概率,需要进行归一化处理: 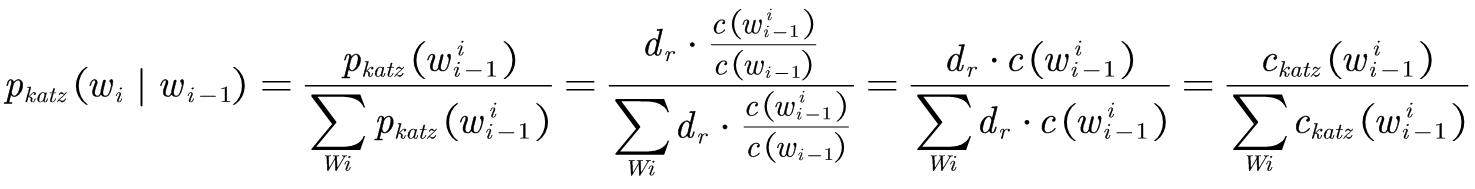
4.Jelinek-Mercer平滑方法
问题的提出:
假定要在一批训练语料上构建二元语法模型,其中,有两对词的出现次数为0:
c(SEND THE)=0
c(SEND THOU)=0
那么按照加法平滑方法和Good-Turing估计方法可以得到:
p(THE|SEND)=p(THOU|SEND)
但是,在我们的直觉上认为应该有:
p(THE|SEND)>p(THOU|SEND)
因为冠词THE要比单词THOU出现的频率高的多。
解决思路:
为了利用这种情况,一种处理思想是在二元语法模型中加入一个一元模型。因为我们知道一元模型实际上只反应在训练文本中单词的出现频率,这恰恰是我们所需要的,最大似然一元模型为:
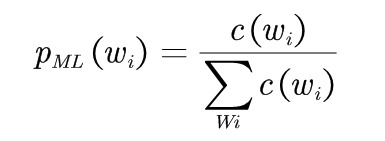
将二元文法模型和一元文法模型进行线性插值:
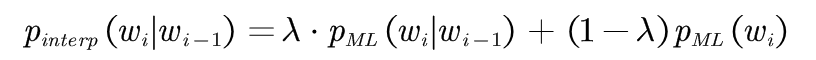 (4-1)
(4-1)
其中,0≤λ≤1。当P(THE|SEND)=P(THOU|SEND)=0 时,根据P(THE)>>P(THOU),可以得到:
 (4-2)
(4-2)
这是我们希望得到的结果。
通常情况下,使用低阶的n元模型向高阶的n元模型插值是有效的,当没有足够的语料估计高阶模型的概率时,低阶模型往往可以提供有用的信息。
1980年Jelinek和Mercer提出了通用插值模型:
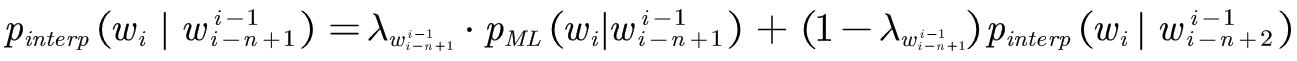
基本思想:第n阶模型可以递归的定义为n阶最大似然估计模型和n-1阶平滑模型之间的线性插值。为了结束递归可以用最大似然分布作为平滑的1阶模型或者用均匀分布作为平滑的0阶模型:
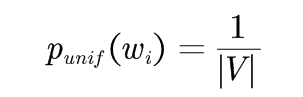






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通