Feedforward Neural Network Language Model(NNLM)原理及数学推导

本文来自CSDN博客，转载请注明出处：http://blog.csdn.net/a635661820/article/details/44130285  

 

参考资料：

词向量部分: http://licstar.net/archives/328#s21

ngram部分: http://www.zhihu.com/question/21661274

论文参考: A Neural Probabilistic Language Model

  

 本文的学习介绍来自一篇Bengio(2003)的论文(点此在线阅读论文PDF), 这篇论文是用神经网络训练语言模型的经典之作，后面我想继续学习RNN，LSTM等，这一篇论文绝对是入门的不错选择。下面是自己对文章的一些理解，毕竟自己刚接触NLP方面的东西，必然有一些不对的地方，还请多多指正。

 

前面一篇MIT的学习笔记介绍了统计语言模型，但传统的统计语言模型有一些缺点：

1. 由于维度灾难(特别是离散变量)，在高维下，数据的稀缺性，导致统计语言模型存在很多为零的条件概率，传统的统计语言模型也花费了很大的精力来处理零概率问题，比如现在有很多的平滑、插值、回退等方法用来解决该问题。
2. 语言模型的参数个数随阶数呈指数增长，所以一般情况统计语言模型使用的阶数不会很高，这样n-gram语言模型无法建模更远的关系。
3. n-gram无法建模出多个相似词的关系。比如在训练集中有这样的句子，The cat is walking in the bedroom，但用n-gram测试时，遇到 A dog was running in a room这个句子，并不会因为两个句子非常相似而让该句子的概率变高。

 

    这篇文章使训练得到的模型比n-gram能够建模更远的关系，并且考虑到了词的相似性，一些相似词获得了自然的平滑。前者是因为神经网络的结构可以使得，后者是因为使用了词向量。

 

 

词向量

 

下面先介绍本文中的词向量(distributed representation for words)，本文中单词的特征向量是把单词映射为一个具有一定维度实数向量(比如50,100维，这里记为m)，每一个词都和一个特征向量相关联，词向量初始化可以为随机的数，文中介绍也可以使用一些先验知识来初始化词向量，随着训练的结束，词向量便获得了。词向量的引入把n-gram的离散空间转换为连续空间，并且两个相似的词之间它们的词向量也相似，所以当训练完毕时，一个句子和其所有相似的句子都获得了概率。而把词映射到词向量是作为整个网络的第一层的，这个在后面会看到。

 

 

神经模型

 

神经网络的模型如图：

 

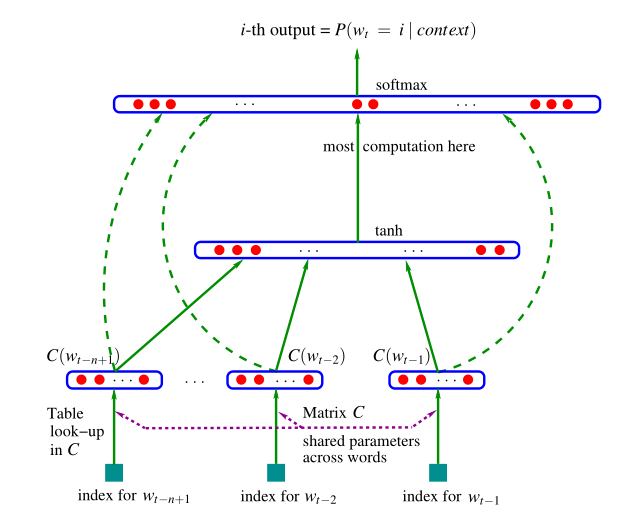
先从整体来看一下模型，其中概率函数表示如下：

 

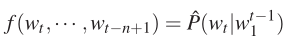
在这个模型中，它可以分解为两部分：

1.  一个 |V|×m映射矩阵C，每一行表示某个单词的特征向量，是m维，共|V|列，即|V|个单词都有对应的特征向量在C中

2.  将条件概率函数表示如下：

 

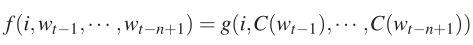
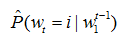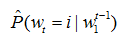即该函数是来估计，其中i有|V|种取值。如果把该网络的参数记作ω，那么整个模型的参数为 θ = (C,ω)。我们要做的就是在训练集上使下面的似然函数最大化：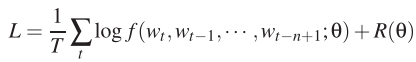

 

下面看一下网络里面的每一层，输出层是用softmax做归一化，这个能够保证概率和为1，如下：

 

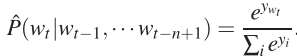
其中yi是未规范化的概率，yi即是输出层的输入，它的计算如下：

 

 

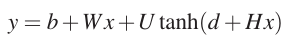
其中Wx表示输入层与输出层有直接联系，如果不要这个链接，直接设置W为0即可，b是输出层的偏置向量，d是隐层的偏置向量，里面的x即是单词到特征向量的映射，计算如下：

 

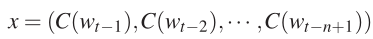
记录隐层的神经元个数为h，那么整个模型的参数可以细化为θ = (b, d, W, U, H, C)。下面计算一下整个模型的参数个数：

输出层偏置向量：|V|

隐层偏置向量：h

隐层到输出层之间的权重矩阵：|V|*h

输入层到输出层的权重矩阵：|V|*(n-1)*m

输入层到隐层的权重矩阵：h*(n-1)*m

特征矩阵C：|V|*m

所有的参数和计算如下：

 

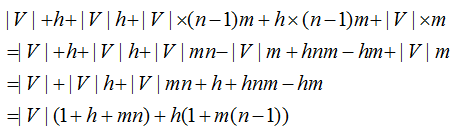
从这个计算式，我们看到网络的参数个数与V是呈线性相关的，与n也是呈线性相关的，而n-gram是指数级递增，这使得论文中的模型可以更有利于建立更远关系的语言模型。

 

模型训练使用的是梯度下降的方式来更新参数：

 

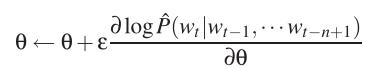
该模型虽然是与V，n线性相关的，但是计算量比n-gram要大得多，由于在输出层的计算量最大，所以论文后面讨论了如何并行使得训练更快。

 

 

模型的算法

 

下面介绍的是模型的算法，因为在我实现的是非并行的算法，这里我略去了并行那块，并且省略了输入层到输出层的直接连接，直接简化了算法。

 

前向算法：

 

(a) 将单词映射为特征向量，该特征向量作为输入层的输出

 

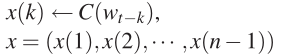
(b)计算隐层的输入向量o，隐层的输出层向量a

 

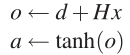
(c)计算输出层输入向量y，输出层输出向量p

 

(d)计算L = logpwt，准备进行反向更新

 

 

反向更新：

 

(a)计算及更新输出层相关量

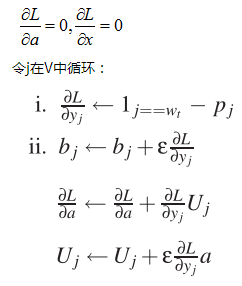
(b)计算及更新隐层

  For k=0 to h-1

        

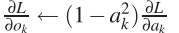
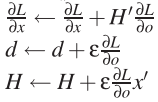
(c)计算及更新输入层

For k=1 to n-1

 

 

 

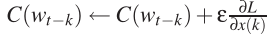
公式推导

 

 

这里将上面反向更新利用的梯度上升进行公式推导