神经网络基础
人工神经元模型
神经网络( neural network )是由模仿神经细胞( neuron )而模型化的称为人工神经元( artificial neuron )的计算元件组合而成的。
生物的神经细胞
生物的神经细胞从其他多个神经细胞获取信号, 在细胞内进行处理, 输出信号给其他神经细胞。
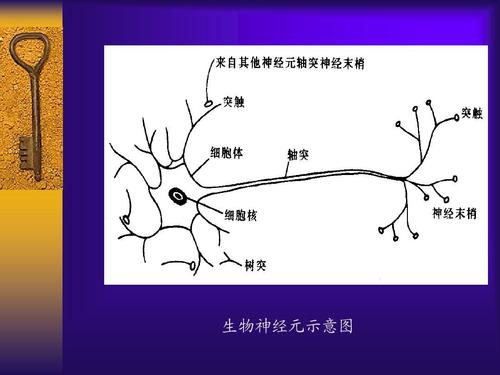
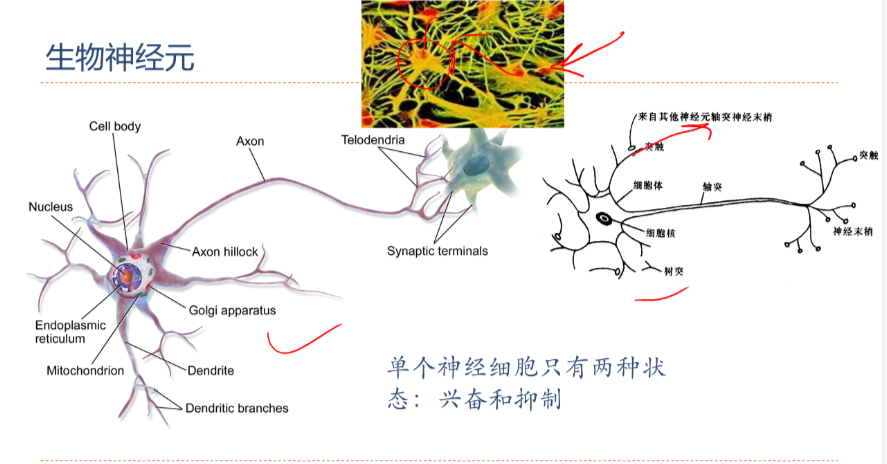
人工神经元是将这一行动简单化后通过数学来模拟的计算元件。

将输入值xi, 和预先确定的与输入相对应的常数Wi 相乘。这个常数W; 称
为权重( weight )。将输入信号和权重相乘后再相加, 减去称为闸值的常数ν 。用符
号u 来表示对输入信号求加权和并减去阈值的值。最后, 通过称为传递函数( transfer
function )的f(u)来处理U, 得到人工神经元的输出Z 。传递函数也称为输出函数(output
function )。
数学公式来表示:
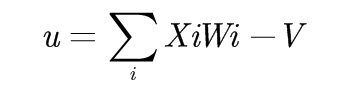

传递函数(激活函数):

●理想激活函数是阶跃函数,0表示抑制神经元而1表示激活神经元
●阶跃函教具有不连续、不光滑等不好的性质、常用的是Sigmoid函教
相同点
●都是非线性函数
●虽然平滑性不同,但宏观上看的形状是相似的,均为“输入小则输出接近0,输入大则输出接近1”
●输出均在0和1之间
不同点
●sigmoid函数的导数在任何地方都不为0。 (这对NN的学 习非常重要;参数们的一点微小的变化也会引起输出的微小的连续的变化,从而使得损失函数可以连续地变化,从而使得参数的更新正常进行,使得NN的学习正确进行)
●而阶跃函数的导数在绝大多数地方(除了0之外)的导数都是0。
●阶跃函数只能返回0或1、而sigmoid可以返回0,1之间的实值。所以感知机中流动的是0,1二元信号,输出随着输入急剧性变化,而NN中流动的是连续的实值信号。
通过具体的例子来看看人工神经元的行为:
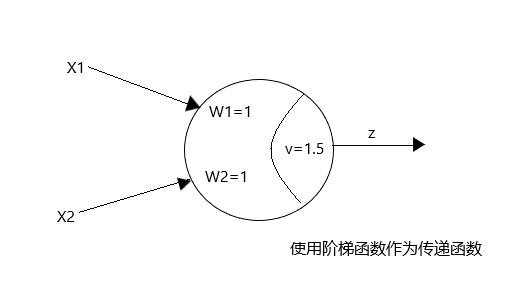
图中是具有两个输入的人工神经元。 作为输入的X1和 X2 接收输入信号, 将之写为( X1, X2 )。这两个输入各自对应的权重是W1和W2 , 在图中, 这两者都是1 阈值为1.5, 传递函数是阶梯函数。
考虑给定输入是(x1, X2) = ( 0, 0)的情形
 =1*0+1*0-1.5=-1.5
=1*0+1*0-1.5=-1.5 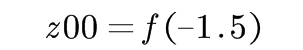 =0
=0
输入( 0, 0)对应的输出是Z00 =0
输入(0,1)、( 1, 0 )以及( 1, 1 ) 所对应的输出为Z01、Z10、Z11
Z01=0,Z10=0, Z11=1
上述人工神经元和AND逻辑运算做了同样的动作
人工神经元中的阔值变更为0.5后, 输出也会发生相应的改变

这次的结果与OR逻辑运算的动作相同。
考虑输入只有一个的人工神经元,权重设为-1阈值设为-0.5, 输入值0和1时, 计算结果如下: =0*(-1)-(-0.5)=0.5
=0*(-1)-(-0.5)=0.5
 =1
=1
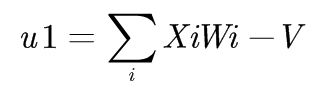 =1*(-1)-(-0.5)=-0.5
=1*(-1)-(-0.5)=-0.5
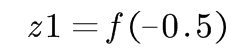 =0
=0
结果和NOT逻辑运算相同。
人工神经元基本上和逻辑算子具有同等的处理能力,适当组合人工神经元可以构建任意的逻辑电路。
多层前馈神经网络
常见的神经网络是形如下图的层级结构,由输入层,隐藏层,输出层构成。
特点:每层神经元与下层神经元完全互连,神经元之间不存在同层连接,也不存在跨层连接。
这样网络也称为前馈神经网络。

当隐藏层只有一层时,该网络为两层神经网络,由于输入层未做任何变换,可以不看做单独的一层。实际中,网络输入层的每个神经元代表了一个特征,输出层个数代表了分类标签的个数(在做二分类时,如果采用sigmoid分类器,输出层的神经元个数为1个;如果采用softmax分类器,输出层神经元个数为2个),而隐藏层层数以及隐藏层神经元是由人工设定。
神经网络的学习过程,就是根据训练数据来调整神经元之间的连接权以及每个功能神经元的阈值,换言之,神经网络学到的东西,蕴涵在连接权和阈值中。





