声道模型传递函数，特征提取（语音线性预测编码，卷积同态系统）

 

                        语音生成的模型

                     

                          

 

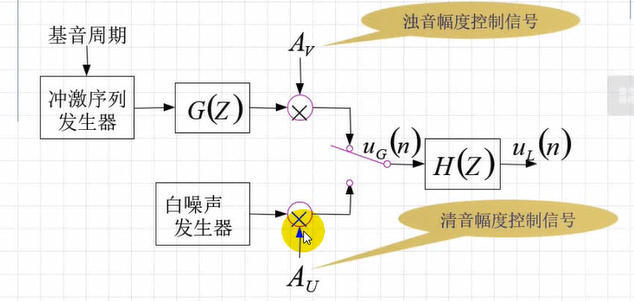
                                                                                声道的传递函数           

                                               

 

 

  

语音线性预测编码(LPC)

                            从语音的产生模型出发，得到H(Z)=

                                                              

                                                                    其中的{ak}是一组非常重要的参数.

 

 

 从变换和反变换角度看,线性预测将语音信息进行压缩，将语音信号用一系列的ak序列进行表示，并可以用ak序列对语音进行合成。

 

                                                         

 

 

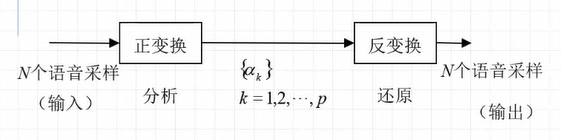
思路与线性预测分析的基本原理

 

 从语音产生模型出发，本身就存在线性组合关系

                                            

 

 

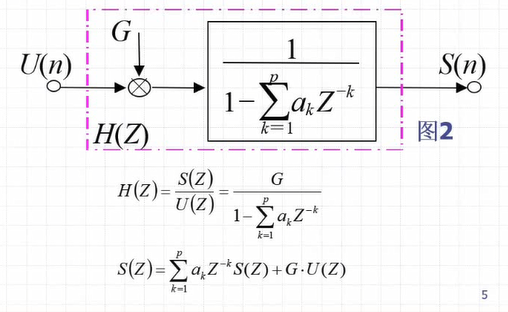
                        对S(Z)进行Z变换的逆变换，写成时间序列表示式为:

 

                                                  

 

如果G*u(n)很小可忽略时，第n个语音采样S(n)是前n-p个采样的线性组合，{ak},k=1,2.....P是线性组合的加权系数。

 假定有一个线性预测器，其系统函数为

   

                                                                      

 

                                                       

                                                                                

 

 

 

          

 

                                                                  引入预测误差  

                                                   

                        

                                

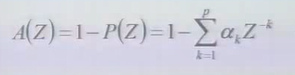
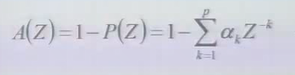                                           逆滤波器

 

                           

 

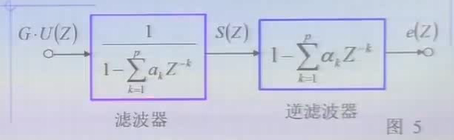
如果线性预测系数选得好，使αk=ak.即有

                       e(Z)=G*U(Z)

即预测误差的Z变换恰好等于输入激励信号序列Z变换、预测误差序列与声道激励序列一对应。

 

 

线性预测的基本问题:

  由语音采样直接决定{αk},并认为{αk}就是{ak}关键问题:  怎样对一段语音求{αk}?

思路如下:

 

 

 

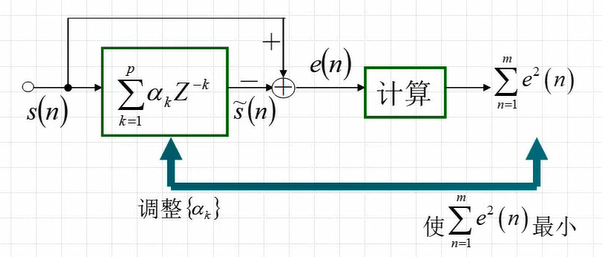
定义:短时平均预测误差

 

 

 

其中s(m)是在n点附近选第m个点的语音，即s(m)=s(n+m)

 

 

 

 

 

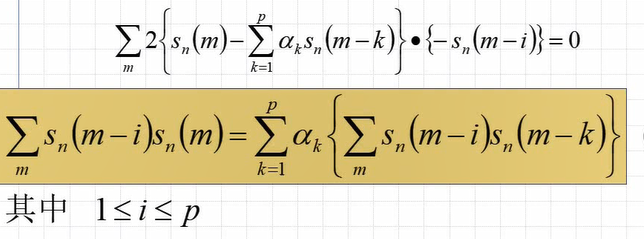
公式3.4的解释:

φn(i, k)反映了语音波形的实际情况，波形不同值不同。{ak}随φn(i, k)变，可以说{ak}反映了波形情况。

 

 

 

 

卷积同态系统

 

“卷积同态系统”的输入输出信号都是卷性信号，即具有相互卷积的关系。

◆同态系统的一个最主要理论结果就是同态系统的分解，分解的目的是用两个特征系统和一个线性系统来代替非线性的同态系统。下图给出了同态系统H(z)的组成。