数据结构与算法（C/C++版）【栈与队列】

第三章《栈与队列》

（一）栈简介  
栈(Stack)：只允许在一端进行插入或删除操作的线性表。首先栈是一种线性表，但是限定这种线性表只能在某一端进行插入和删除操作
栈顶(top)：线性表允许进行插入和删除的那一端。（开口的那一端）
栈底(bottom)：固定的，不允许进行插入和删除的另一端。（封死的那一端）
空栈：不含任何元素的空表。

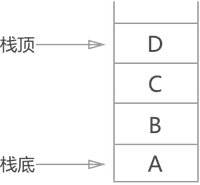
栈的“先进后出”原则（FILO）：已上图为例，栈中存放了 4 个数据元素，进栈的顺序是 A 先进栈，然后 B 进，然后 C 进，最后 D 进栈；当需要调取 A 时，首先 D 出栈，然后 C 出栈，然后 B 出栈，最后 A 才能出栈被调用。

栈的两种表示方式：栈的本质是线性表，那么它就同样有线性表的两种表示形式：顺序栈 和 链式栈（简称“链栈”）
两者的区别：存储的数据元素在物理结构上是否是相互紧挨着的。顺序栈存储元素预先申请连续的存储单元；链栈需要即申请，数据元素不紧挨着。

栈的“上溢”和“下溢”问题：
“上溢”：在栈已经存满数据元素的情况下，如果继续向栈内存入数据，栈存储就会出错。（栈满还存会“上溢”）
“下溢”：在栈内为空的状态下，如果对栈继续进行取数据的操作，就会出错。（栈空再取会“下溢”）
对于栈的两种表示方式来说，顺序栈两种情况都有可能发生；而链栈由于“随时需要，随时申请空间”的存储结构，不会出现“上溢”的情况。

栈的基本操作：
　　InitStack(&S)：初始化一个空栈S。
　　StackEmpty(S)：判断一个栈是否为空，若栈S为空返回true，否则返回false。
　　Push(&S, x)：进栈，若栈S未满，将x加入使之成为新桟顶。
　　Pop(&S, &x)：出栈，若栈S非空，弹出栈顶元素，并用x返回。
　　GetTop(S, &x)：读栈顶元素，若栈S非空，用x返回栈顶元素。
　　ClearStack(&S)：销毁栈，并释放栈S占用的存储空间。
注意：符号'&'是C++特有的，用来表示引用，有的书上釆用C语言中的指针类型‘*’，也可以达到传址的目的。

 

（二）顺序栈  

1、简介

定义：栈的顺序存储称为顺序栈，它是利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针(top)指示当前栈顶的位置。

(a)是空栈，(c)是A、B、C、D、E共5 个元素依次入栈后的结果，(d)是在图3-2 (c)之后E、D、C相继出栈，此时栈中还 有2个元素，或许最近出栈的元素C、D、E仍在原先的单元存储着，但top指针已经指向了 新的栈顶，则元素C、D、E已不在栈中了，

栈顶指针：S.top，初始时设置S.top=-1；栈顶元素：S.data[S.top]。
进栈操作：栈不满时，栈顶指针先加1，再送值到栈顶元素。
出栈操作：栈非空时，先取栈顶元素值，再将栈顶指针减1。
栈空条件：S.top=-1；栈满条件：S.top==MaxSize-1；栈长：S.top+1。

2、常见操作

① 结构体定义

#define MaxSize 50           //定义栈中元素的最大个数
typedef struct{
    Elemtype data[MaxSize];  //存放栈中元素
    int top;                 //栈顶指针
}SqStack;

② 初始化

void initStack(Sqstack &st)
{
    st.top=-1;               //初始化栈顶指针
}

③ 判断是否为空

void isEmpty(Sqstack st)
{
    if(st.top==-1)          //栈空
        return 1;
    else                    //不空
        return 0;
}

④ 进栈

int push(Sqstack &st,int &x)
{
    if(st.top==maxSize-1)   //栈满，报错
        return 0;
    ++(st.top);             //指针先加 1（先移动指针），再进栈
    st.data[st.top]=x;
    return 1;
}

⑤ 出栈

int pop(Sqstack &st,int &x)
{
    if(st.top==-1)          //栈空，报错
        return 0;
    x=st.data[st.top];      //先出栈，指针再减1（先取出元素，在移动指针）
    --(st.top);
    return 1;
}

⑥ 读栈顶元素

bool GetTop(SqStack S,ElemType &x){
    if (S.top==-1)     //找空，报错
        return false;
    x=S.data[S.top];  //x记录栈顶元素
    return true;
}

⑦ 简化写法

//1.初始化
int stack[maxSize];
int top=-1;
//2.进栈
stack[++top]=x;
//3.出栈
x=stack[--top];

3、共享栈
利用栈底位置相对不变的特性，可以让两个顺序栈共享一个一维数据空间，将两个栈的 栈底分别设置在共享空间的两端，两个栈顶向共享空间的中间延伸。

两个栈的栈顶指针都指向栈顶元素，top0=-1 时0号桟为空，top1=MaxSize时1号栈为空；仅当两个栈顶指针相邻(top1-top0=1) 时，判断为栈满。当0号栈进栈时top0先加1 再赋值，1号栈进栈时top1先减1再赋值；出栈时则刚好相反。

共享栈是为了更有效地利用存储空间，两个栈的空间相互调节，只有在整个存储空间被 占满时才发生上溢。其存取数据的时间复杂度均为0(1)，所以对存取效率没有什么影响。

 

（三）链栈  

釆用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高其效率，且 不存在栈满上溢的情况。通常釆用单链表实现，并规定所有操作都是在单链表的表头进行的。 这里规定链栈没有头结点（链栈一般不需要创建头结点，头结点会增加程序的复杂性，只需要创建一个头指针就可以了），Lhead指向栈顶元素。

1、常见操作

① 初始化

void initStack(LNode*&lst)               //lst要改变，用引用型
{
    lst=(LNode*)malloc(sizeof(LNode));   //创建一个头结点
    lst->next=NULL;
    
}

② 判断是否为空

void isEmpty(Sqstack *lst)
{
    if(lst->next==NULL)     //栈空
        return 1;
    else                    //不空
        return 0;
}

③ 进栈

int push(Sqstack *lst,int x)
{
    LNode *p;
    p=(LNode*)malloc(sizeof(LNode)); //为进栈元素申请结点空间(默认内存无限大)
    p->next=NULL;                    //初始化（没新申请一个结点，将其指针域设置为NULL）
    
    //以下是单链表的头插法
    p->next =x;     
    p->next =lst->next;
    lst->next=p;
}

④ 出栈

int pop(Sqstack *lst,int &x)
{
    LNode *p;
    if(lst->next==NULL)      //栈空不能出栈
        return=0;
    
    //以下是单链表的删除操作
    p=(LNode*)malloc(sizeof(LNode)); //为进栈元素申请结点空间
    p->next=NULL;                    //初始化（没新申请一个结点，将其指针域设置为NULL）
    
    //以下是链表的头插法
    p = lst->next; 
    x=p->data;
    lst->next=p->next;
    free(p);
    return 1;
}

 

（四）队列简介  

队列(Queue)：队列简称队，也是一种操作受限的线性表，只允许在表的一端进行插入，而在表的另一端进行删除。

“先进先出”（FIFO）：这和我们日常生活中的排队是一致的，最早排队的也是最早离队的。
队头(Front)：允许删除的一端，又称为队首。
队尾(Rear)：允许插入的一端。
空队列：不含任何元素的空表。

队列常见的基本操作：
　　InitQueue(&Q)：初始化队列，构造一个空队列Q。
　　QueueEmpty(Q)：判队列空，若队列Q为空返回true，否则返回false。
　　EnQueue(&Q, x)：入队，若队列Q未满，将x加入，使之成为新的队尾。
　　DeQueue(&Q, &x)：出队，若队列Q非空，删除队头元素，并用x返回。
　　GetHead(Q, &x)：读队头元素，若队列Q非空，则将队头元素赋值给X。
需要注意的是，队列是操作受限的线性表，所以，不是任何对线性表的操作都可以作为队列的操作。比如，不可以随便读取队列中间的某个数据。

 

（五）顺序队列、循环队列  

<1>顺序队列

队列的顺序实现是指分配一块连续的存储单元存放队列中的元素，并附设两个指针front 和rear分别指示队头元素和队尾元素的位置。设队头指针指向队头元素，队尾指针指向队尾 元素的下一个位置（也可以让rear指向队尾元素，front指向队头元素的前一个位置）

结构体定义：

#define MaxSize 50           //定义队列中元素的最大个数
typedef struct{
    ElemType data[MaxSize];  //存放队歹I]元素
    int front, rear;         //队头指针和队尾指针
}SqQueue;

初始状态（队空条件）：Q.front==Q.rear==0。
进队操作：队不满时，先送值到队尾元素，再将队尾指针加1。
出队操作：队不空时，先取队头元素值，再将队头指针加1。

(a)所示为队列的初始状态，有Q.front==Q.rear==0成立，该条件可以作为队列判空的条件。但能否用Q.rear==MaxSize作为队列满的条件呢？显然不能，图3-6(d)中， 队列中仅有1个元素，但仍满足该条件。这时入队出现“上溢出”，但这种溢出并不是真正 的溢出，在data数组中依然存在可以存放元素的空位置，所以是一种“假溢出”。

<2>循环队列

为了解决顺序队列的缺点将顺序队列变为一个环状的空间，即把存储队列元素的表从逻辑上看成一个环,称为循环队列。当队首指针Q.ftont =MaxSiZe-1后，再前进一个位置就自动到0，这可以利用除法取余运算(%)来实现。

　　初始时：Q.front=Q.rear=0
　　队首指针进 1：Q.front=(Q.front+1)%MaxSize
　　队尾指针进 1：Q.rear=(Q.rear+1)%MaxSize
　　队列长度：(Q.rear+MaxSize-Q.front)%MaxSize
　　出队入队时：指针都按顺时针方向进1

那么，循环队列队空和队满的判断条件是什么呢？显然，队空的条件是Q.front==Q.rear。 如果入队元素的速度快于出队元素的速度，队尾指针很快就赶上了队首指针，如图(d1)，此时可以看出队满时也有Q.front==Q.rear。

为了区分队空还是队满的情况，有三种处理方式：
　　1) 牺牲一个单元来区分队空和队满，入队时少用一个队列单元，这是一种较为普遍的做法，约定以“队头指针在队尾指针的下一位置作为队满的标志”，如图(d2)所示。
　　　　队满条件为：   (Q.rearfl)%MaxSize==Q.front。
　　　　队空条件仍为：Q.front==Q.rear。
　　　　队列中元素的个数：(Q.rear-Q.front+MaxSize)%MaxSize
　　2) 类型中增设表示元素个数的数据成员。这样，则队空的条件为Q.Size==0，队满的条 件为 Q.size==MaxSize。这两种情况都有 Q.front=Q.rear。
　　3) 类型中增设tag数据成员，以区分是队满还是队空。tag等于0的情况下，若因删除导致Q.front==Q.rear则为队空；tag等于1的情况下，若因插入导致Q.ftont==Q.rear则为队满。

 循环队列的操作：

①初始化

void InitQueue(&Q)
{
    Q.rear=Q.front=0;  //初始化队首、队尾指针
}

②判队空

bool isEmpty(Q) 
{
    if(Q.rear == Q.front) //队空条件
        return true;  
    else 
        return false;
}

③入队

bool EnQueue(SqQueue &Q, ElemType x)
{
    if((Q.rear+1)%MaxSize == Q.front) //队满
        return false; 
    Q.rear= (Q.rear+1)%MaxSize;       //队未满（先移动指针）
    Q.data[Q.rear]=x;                 //（再存入数据）
    return true;
}

④出队

bool DeQueue(SqQueue &Q, ElemType &x)
{
    if(Q.rear == Q.front) 
        return false;                  //队空，报错
    Q.front= (Q.front+1)%MaxSize;      //队不空（先移动指针）
    x=Q.data[Q.front];                 //（再存入数据）
    return true;
}

 

（六）链队  

队列的链式表示称为链队列，它实际上是一个同时带有队头指针和队尾指针的单链表。头指针指向队头结点，尾指针指向队尾结点，即单链表的最后一个结点。

不设头结点的链式队列在操作上往往比较麻烦，因此，通常将链式队列设计 成一个带头结点的单链表，这样插入和删除操作就统一了。

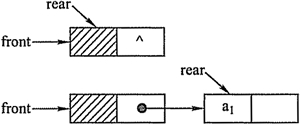
用单链表表示的链式队列特别适合于数据元素变动比较大的情形，而且不存在队列满且产生溢出的问题。另外， 假如程序中要使用多个队列，与多个栈的情形一样，最好使用链式队列，这样就不会出现存储分配不合理和“溢出” 的问题。

链式队列的基本操作（跟线性表类似）：

① 初始化

void InitQueue(LinkQueue &Q)
{
    Q.front = Q.rear=(LinkNode*)malloc(sizeof(LinkNode));  //创建头结点
    Q.front->next=NULL;                                    //初始为空
}

② 判队空

bool IsEmpty(LinkQueue Q)
{
    if(Q.front==Q.rear) 
        return true;
    else 
        return false;
}

③入队

③入队
void EnQueue(LinkQueue &Q, ElemType x)
{
    s=(LinkNode *)malloc(sizeof(LinkNode));//创建新结点
    s->data=x; 
    s->next=NULL;  
    Q.rear->next=s;   //插入到链尾
    Q.rear=s;
}

④出队

bool DeQueue(LinkQueue &Q, ElemType &x)
{
    if (Q.front == Q.rear) 
        return false;     //空队
    p=Q.front->next;
    x=p->data;
    Q.front->next=p->next;
    if(Q.rear==p)
        Q.rear=Q.front;  //若原队列中只有一个结点，删除后变空
    free(p);
    return true;
}

 

（七）双端队列  

双端队列是指允许两端都可以进行入队和出队操作的队列。其元素的 逻辑结构仍是线性结构。将队列的两端分别称为前端和后端，两端都可以入队和出队。

进队时：前端进的元素排列在队列中后端进的元素的前面，后端进的元素排列在队列中前端进的元素的后面。
出队时：无论前端还是后端出队，先出的元素排列在后出的元素的前面。

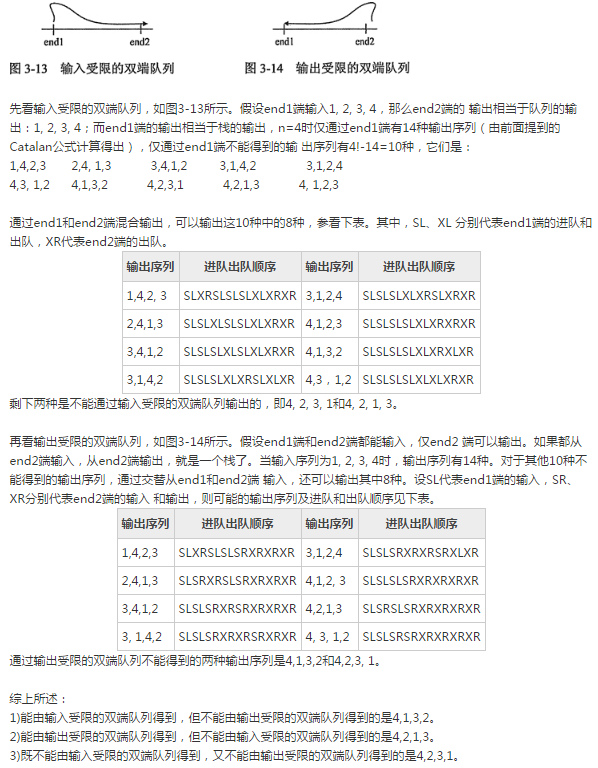
①输出受限的双端队列：允许在一端进行插入和删除，但在另一端只允许插入的双端队列。

②输入受限的双端队列：允许在一端进行插入和删除，但在另一端只允许删除的双端队列。而如果限定双端队列从某个端点插入的元素只 能从该端点删除，则该双端队列就蜕变为两个栈底相邻接的栈了。

 

 

 

（八）栈的应用：

①括号匹配
②表达式求值
③递归

 （九）队列的应用：

①层次遍历
②解决主机与外部设备之间速度不匹配问题
③解决由多用户引起的资源竞争问题

关于应用以后有时间回来补充。。。。