二分查找法

二分法

分析 大神的视频讲解链接

1. 常见的查找边界问题：

   

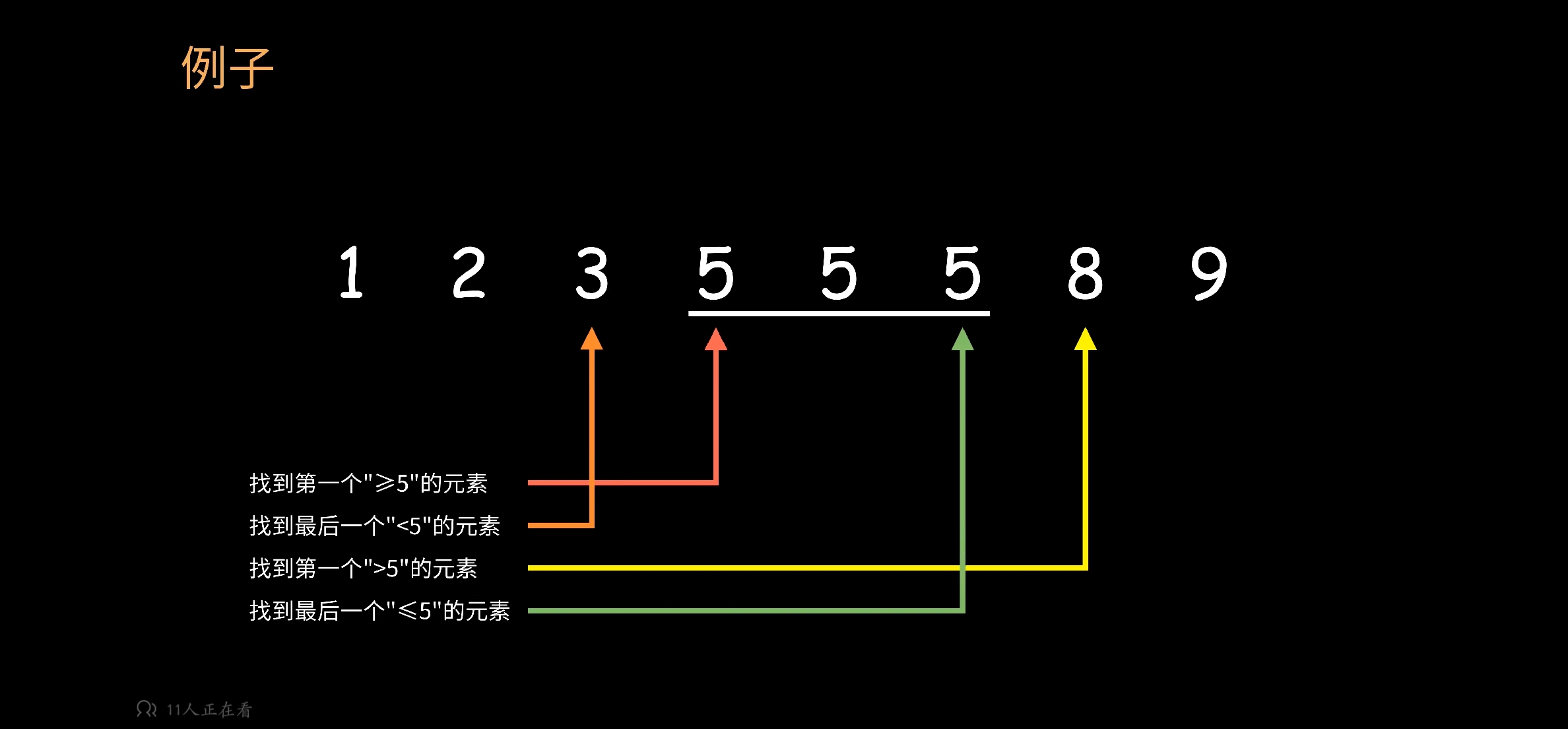
2. 最不易出错的解法：

   初始l、r设为数组边界两端分别往外扩展一个单位，这样可以保证数组长度只有1位或其它情况时不会陷入死循环。

3. 伪代码：

   // 以数组int a[N]为例，实际数据所在下标为0~N-1
   l = -1, r = N;
   while l + r != r{
       m = l + r >> 1;
       if IsBlue(m)
           l = m;
       else
           r = m;
   }
   return l or r;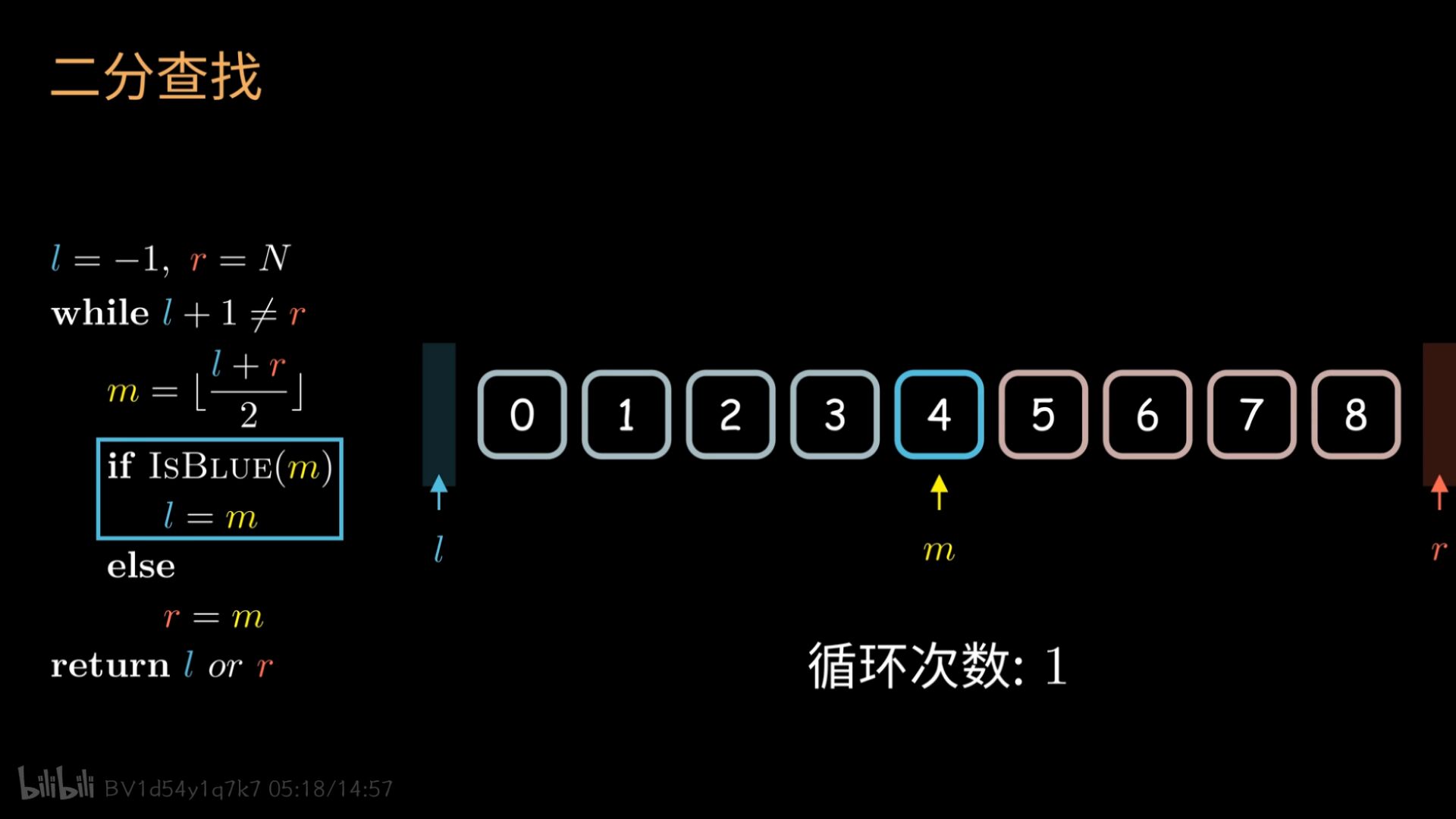
   

   

4. 伪代码完善：

   {{uploading-image-636625.png(uploading...)}}

示例

1. 题干：

   给定一个按照升序排列的长度为 nn 的整数数组，以及 qq 个查询。

   对于每个查询，返回一个元素 kk 的起始位置和终止位置（位置从 00 开始计数）。

   如果数组中不存在该元素，则返回 -1 -1。

   输入格式

   第一行包含整数 nn 和 qq，表示数组长度和询问个数。

   第二行包含 nn 个整数（均在 1∼100001∼10000 范围内），表示完整数组。

   接下来 qq 行，每行包含一个整数 kk，表示一个询问元素。

   输出格式

   共 qq 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

   如果数组中不存在该元素，则返回 -1 -1。

   数据范围

   1≤n≤1000001≤n≤100000
   1≤q≤100001≤q≤10000
   1≤k≤100001≤k≤10000

   输入样例：

   6 3
   1 2 2 3 3 4
   3
   4
   5
   

   输出样例：

   3 4
   5 5
   -1 -1
   

2. 代码：

   #include<bits/stdc++.h>
   using namespace std;
   const int N = 100010;
   int n, q;
   int f[N];
   
   int find_L(int L, int R, int x){
       int l = L - 1, r = R + 1;
       while(l + 1 != r){
           int mid = l + r >> 1;
           if(x > f[mid]) l = mid;
           else r = mid;
       }
       if(f[r] == x) return r - 1;
       else return -1;
   }
   
   int find_R(int L, int R, int x){
       int l = L - 1, r = R + 1;
       while(l + 1 != r){
           int mid = l + r >> 1;
           if(x >= f[mid]) l = mid;
           else r = mid;
       }
       if(f[l] == x) return l - 1;
       else return -1;
   }
   
   
   int main(){
       scanf("%d%d", &n, &q);
       for(int i = 1; i <= n; i ++) scanf("%d", f + i);
       while(q --){
           int k;
           scanf("%d", &k);
           printf("%d %d\n", find_L(1, n, k), find_R(1, n, k));
       }
       
       return 0;
   }