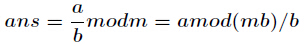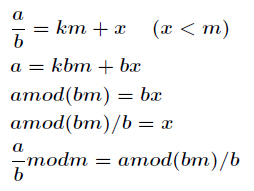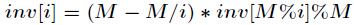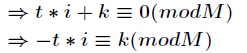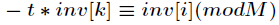求逆元
一篇对逆元不错的讲解https://blog.csdn.net/acdreamers/article/details/8220787
逆元:对于a和p(a和p互素),若a*b%p≡1,则称b为a%p的逆元
(1)用扩展欧几里得求逆元
时间复杂度为O(log n)
#include<bits/stdc++.h>
using namespace std;
#define ios1 std::ios::sync_with_stdio(false)
#define ios2 std::cin.tie(0)
#define inf 0x3f3f3f3f
#define ll long long
ll ex_gcd(ll a,ll b,ll &x,ll &y)
{
if(b == 0)
{
x = 1;
y = 0;
return a;
}
ll gcd = ex_gcd(b,a%b,y,x);
y -= a/b * x;
return gcd;
}
int main()
{
ll a, m, x, y;
scanf("%lld%lld", &a, &m);//求a对m的逆元
if(ex_gcd(a, m, x, y) == 1) printf("%lld\n",(x%m+m)%m);
else printf("0\n");
return 0;
}
(2)用费马小定理求逆元
时间复杂度为O(log n)
#include<bits/stdc++.h>
using namespace std;
#define ios1 std::ios::sync_with_stdio(false)
#define ios2 std::cin.tie(0)
#define inf 0x3f3f3f3f
#define ll long long
ll qpow(ll a, ll b, ll m)//快速幂
{
ll ans = 1;
a %= m;
while(b > 0)
{
if(b & 1)
ans = (ans * a) % m;
a = a * a % m;
b >>= 1;
}
return ans;
}
ll Fermat(ll a, ll p)//前提p是质数
{
return qpow(a,p-2,p);
}
int main() {
ll a, m, i;
scanf("%lld%lld", &a, &m);
printf("%lld\n", Fermat(a, m));
return 0;
}
(3)由于前两种都有局限性,所以有一种通用的方法求逆元
求现在来看一个逆元最常见问题,求如下表达式的值(已知
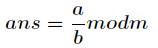
当然这个经典的问题有很多方法,最常见的就是扩展欧几里得,如果
但是你会发现费马小定理和扩展欧几里得算法求逆元是有局限性的,它们都会要求

种通用的求逆元方法,适合所有情况。公式如下
现在我们来证明它,已知
(4)线性求逆元
其实有些题需要用到


如果对于一个1000000级别的素数
它的推导过程如下,设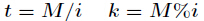
对上式两边同时除
再把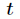
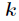
初始化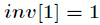


另外


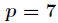
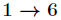
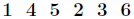
#include<bits/stdc++.h>
using namespace std;
#define ios1 std::ios::sync_with_stdio(false)
#define ios2 std::cin.tie(0)
#define inf 0x3f3f3f3f
#define ll long long
const ll maxn = 4e6 + 10;
ll inv[maxn];
int main()
{
ll n,m,i;
scanf("%lld%lld", &n, &m);
inv[1]=1;
for(i=2;i<=n;i++)
inv[i]=(m-m/i)*inv[m%i]%m;
for(i = 1; i <= n; i++){
printf("%lld\n", inv[i]);
}
return 0;
}