【瞎口胡】半平面交
顾名思义,用于求解若干半平面的交。
在 OI 中,一般有如下的应用情形:给定若干条直线,求它们的左边组成的半平面的交。
事实上,我们可以通过一组点集来描述半平面交:这是因为如果半平面交的面积有限,那么它一定是凸多边形。证明可以考虑找到多边形中一个大于 \(180\) 度的角,然后很容易发现这是不符合条件的。
流程
考虑构造半平面交。我们将所有直线极角排序,然后依次加入。我们维护一个双端队列表示当前构成半平面交的直线。
一般来讲,加入一条直线,我们无事发生:
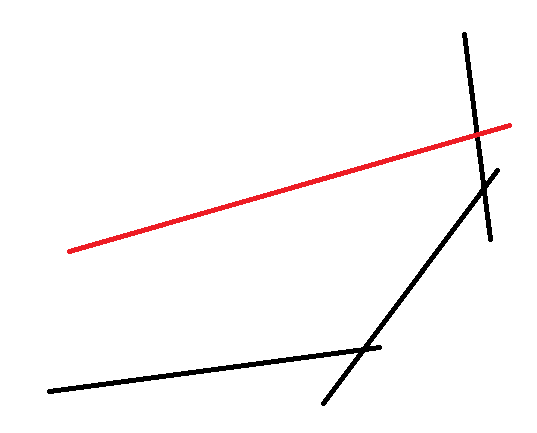
它会和之前的直线(黑色)一起构成当前的半平面交。
但意外总会发生。
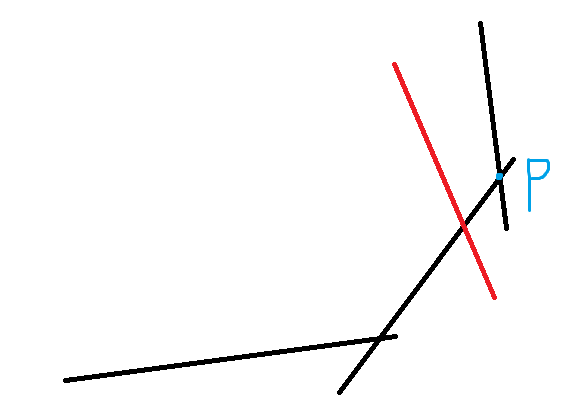
如图,当前队尾的两条直线的交点在红色直线的右侧。此时我们可以断定,队尾的直线对构成半平面交没有贡献,因为红色的限制严格强于它。因此,我们 Pop 掉队尾的直线。
不止队尾,队首的直线可能也会被 Pop 掉。
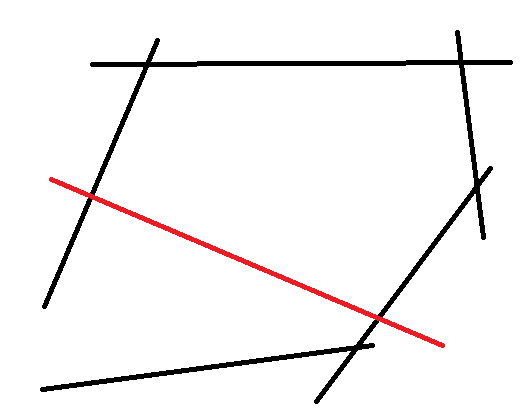
只需要判定队首两条直线的交点是否在红色直线右侧。
另外,加完所有直线后,还应该依次判定队尾两条直线的交点是否在队首直线的左侧,如果是,则 Pop 队尾。原因很简单,加入直线时,前面的直线受后面直线约束,但后面的直线不受前面直线的约束。但它们连成的是一个环,因此队尾的直线是要受到队首直线约束的。
注意事项
我们操作时应该先 Pop 队尾再 Pop 队首,原因见 OI-Wiki。
如果有多个共线的直线,我们应该直接最左侧的。实现细节见代码。
# include <bits/stdc++.h>
# define Vector Point
# define DB double
# define CP const Point
# define CV const Vector
const int N=100010,INF=0x3f3f3f3f;
const DB eps=1e-8;
const DB Pi=acos(-1);
struct Point{
DB x,y;
Point(DB X=0,DB Y=0){
x=X,y=Y;
return;
}
};
struct dLine{
Point s,t;
double an;
};
dLine que[N];
typedef std::vector <Point> Poly;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-')f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
inline int Sign(DB x){
return (x<-eps)?-1:((x>eps)?1:0);
}
inline bool x_comp(CP &a,CP &b){
return (Sign(a.x-b.x))?(a.x<b.x):(a.y<b.y);
}
inline DB Fabs(DB x){
return x*Sign(x);
}
inline DB Dot(CV &u,CV &v){
return u.x*v.x+u.y*v.y;
}
inline DB Cro(CV &u,CV &v){
return u.x*v.y-u.y*v.x;
}
inline DB Len(CV &u){
return sqrt(Dot(u,u));
}
Vector operator - (CV &u,CV &v){
return Vector(u.x-v.x,u.y-v.y);
}
Vector operator + (CV &u,CV &v){
return Vector(u.x+v.x,u.y+v.y);
}
Vector operator * (CV &u,DB k){
return Vector(u.x*k,u.y*k);
}
bool operator == (CP &u,CP &v){
return !(Sign(u.x-v.x)||Sign(u.y-v.y));
}
inline Point PointTurn(CP &u,DB theta){
return Point(u.x*cos(theta)+u.y*sin(theta),-u.x*sin(theta)+u.y*cos(theta));
}
inline Point PointTurn(CP &u,DB theta,CP &c){
return Point((u.x-c.x)*cos(theta)+(u.y-c.y)*sin(theta)+c.x,-(u.x-c.x)*sin(theta)+(u.y-c.y)*cos(theta)+c.y);
}
inline bool PointonSeg(CP &u,CP &a,CP &b){
return !Sign(Cro(u-a,u-b))&&(Dot(u-a,u-b)<=0);
}
inline bool DistoSeg(CP &u,CP &a,CP &b){
if(a==b)
return Len(u-a);
Vector au=u-a,bu=u-b,ab=b-a;
if(Sign(Dot(au,ab))<0)
return Len(au);
if(Sign(Dot(bu,ab))>0)
return Len(bu);
return Fabs(Cro(au,ab)/Len(ab));
}
inline bool PointonLine(CP &u,CP &a,CP &b){
return !Sign(Cro(u-a,u-b));
}
inline Point FootPoint(CP &u,CP &a,CP &b){
Vector au=u-a,bu=u-b,ab=b-a;
DB aulen=Dot(au,ab)/Len(ab),bulen=-1.0*Dot(bu,ab)/Len(ab);
return a+ab*(aulen/(aulen+bulen));
}
inline Point SymPoint(CP &u,CP &a,CP &b){
return u+(FootPoint(u,a,b)-u)*2;
}
inline Point CrossLL(CP &a,CP &b,CP &c,CP &d){
Vector ab=b-a,cd=d-c,ca=a-c;
// printf("%.8lf\n",Cro(ab,cd));
// if(Sign(Cro(ab,cd))==0)
// printf("warning\n");
return a+ab*(Cro(cd,ca)/Cro(ab,cd));
}
inline bool CrossLS(CP &a,CP &b,CP &c,CP &d){
return (PointonLine(CrossLL(a,b,c,d),c,d));
}
inline bool CrossSS(CP &a,CP &b,CP &c,CP &d){
DB ab_c=Cro(b-a,c-a),ab_d=Cro(b-a,d-a);
DB cd_a=Cro(d-c,a-c),cd_b=Cro(d-c,b-c);
return (Sign(ab_c)*Sign(ab_d)<0)&&(Sign(cd_a)*Sign(cd_b)<0);
}
inline DB PolyArea(Poly &P){
if(P.size()<=2) return 0;
DB res=0;
for(int i=0;i<(int)P.size();++i){
res+=Cro(P[i],P[(i+1)%P.size()]);
}
return res/2.0;
}
inline void ConvexHull(Poly &P,Poly &ans){
int n=P.size();
std::sort(P.begin(),P.end(),x_comp);
ans.resize(0);
int siz=0;
for(int i=0;i<n;++i){
while(siz>1&&Sign(Cro(ans[siz-1]-ans[siz-2],P[i]-ans[siz-2]))<=0)
--siz,ans.pop_back();
ans.push_back(P[i]),++siz;
}
for(int i=n-1,st=siz;i>=0;--i){
while(siz>st&&Sign(Cro(ans[siz-1]-ans[siz-2],P[i]-ans[siz-2]))<=0)
--siz,ans.pop_back();
ans.push_back(P[i]),++siz;
}
ans.pop_back();
return;
}
inline DB PolyDiameter(Poly &P){
int n=P.size();
if(P.size()<2)
return 0;
if(P.size()==2)
return Len(P[0]-P[1]);
int now=2;
DB res=0;
P.push_back(P[0]);
for(int i=0;i<n;++i){
while(Sign(Cro(P[i+1]-P[i],P[now]-P[i])-Cro(P[i+1]-P[i],P[now+1]-P[i]))<0)
now=(now+1)%n;
res=std::max(res,std::max(Len(P[now]-P[i]),Len(P[i+1]-P[i])));
}
P.pop_back();
return res;
}
inline bool DvecComp(const dLine &u,const dLine &v){
if(Sign(u.an-v.an)){
return Sign(u.an-v.an)==-1;
}
return Sign(Cro(u.t-u.s,v.t-u.s))==1; // 如果 v 在 u 的左边,则叉积>0,u 排在 v 之前
}
inline bool AngleCheck(const dLine &u,const dLine &v,const dLine &z){ // check if uv at the right of z
Point cro=CrossLL(u.s,u.t,v.s,v.t);
return Sign(Cro(cro-z.s,z.t-z.s))==1;
}
inline Poly HalfPlane(std::vector <dLine> &Lines){
int siz=Lines.size();
for(int i=0;i<siz;++i){
Lines[i].an=atan2(Lines[i].t.y-Lines[i].s.y,Lines[i].t.x-Lines[i].s.x);
}
std::sort(Lines.begin(),Lines.end(),DvecComp); // 极角排序
Poly ans;
int l=1,r=0;
for(int i=0;i<siz;++i){
while(l<r&&AngleCheck(que[r-1],que[r],Lines[i]))
--r;
while(l<r&&AngleCheck(que[l],que[l+1],Lines[i]))
++l;
que[++r]=Lines[i];
if(l<r&&!Sign(Cro(que[r].t-que[r].s,que[r-1].t-que[r-1].s))) // 平行时,一定是后面的直线更靠左
--r,que[r]=Lines[i]; // 将原来的直线更换为自己,队列长度 --
}
while(l<r&&AngleCheck(que[r-1],que[r],que[l])) // 检查队尾
--r;
for(int i=l;i<r;++i)
ans.push_back(CrossLL(que[i].s,que[i].t,que[i+1].s,que[i+1].t));
ans.push_back(CrossLL(que[r].s,que[r].t,que[l].s,que[l].t));
return ans;
}
int main(void){
std::vector <dLine> S;
Poly P;
int T=read(),n;
while(T--){
n=read();
P.clear();
for(int i=1;i<=n;++i){
int x=read(),y=read();
P.push_back((Point){1.0*x,1.0*y});
}
for(int i=0;i<(int)P.size();++i){
S.push_back((dLine){P[i],P[(i+1)%P.size()],0.0});
}
}
Poly res=HalfPlane(S);
printf("%.3lf",PolyArea(res));
return 0;
}

