【瞎口胡】快速傅里叶变换 / FFT
快速傅里叶变换(FFT)是一种在 \(O(n \log n)\) 时间复杂度内求出两个 \(n\) 次多项式乘积的算法。
系数表示法和点值表示法
对于 \(n\) 次多项式 \(f(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n\),如果我们知道了每一个 \(a_i\),那么这个多项式就唯一确定。于是我们用系数序列 \(a=\{a_0,a_1,a_2,\cdots,a_n\}\) 来表示这个多项式,这被称作系数表示法。
而我们也可以取这个多项式在 \(n+1\) 个不同的 \(x\) 处的取值来表示这个多项式。根据高斯消元法,这 \(n+1\) 个 \(x\) 以及 \(f(x)\) 的取值可以确定这个多项式。这被称作点值表示法。
一个多项式从系数表示法转换为点值表示法的过程,被称作离散傅里叶变换(DFT)。反之则是离散傅里叶逆变换(IDFT)。
FFT 取一些特殊的 \(x\),来加速 DFT 和 IDFT 的过程。这些 \(x\) 甚至不在实数域,而是一些复数。
特殊的复数
在复平面上,一个以原点为圆心,半径为 \(1\) 的圆被称作单位圆。从实轴(\(x\) 轴)正方向开始,逆时针作 \(n\) 个向量将单位圆 \(n\) 等分,则这些向量与单位圆相交形成的 \(n\) 个交点被称作 \(n\) 次复根,第一个辐角为正的向量与单位圆的交点被称作 \(n\) 次单位复根,记作 \(\omega_n\)。
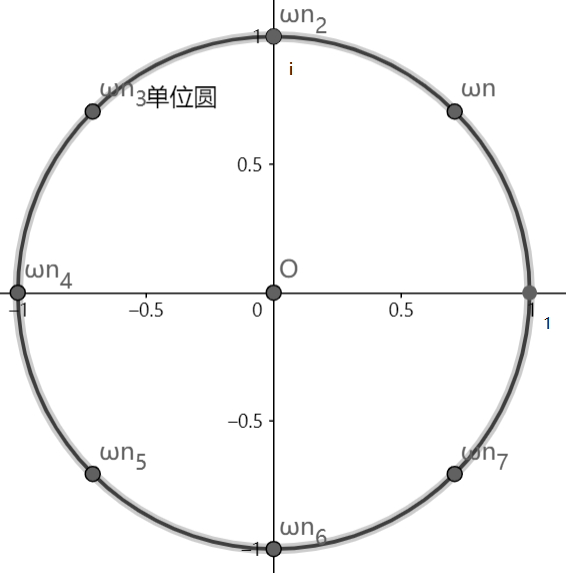
根据复数的乘法运算法则「模长相乘,辐角相加」,可知 \(n\) 次复根的 \(n\) 次方都是 \(1\)。而所有 \(n\) 次复根都可以用 \(n\) 次单位复根的幂表示。
我们知道,\(2 \pi \operatorname{rad} = 360^\circ\)。根据三角函数的知识,\(\omega_n\) 的实部即为 \(\cos(\dfrac{2\pi}{n})\),虚部为 \(\sin(\dfrac{2\pi}{n})\)。于是,\(\omega_n=\cos(\dfrac{2\pi}{n})+\sin(\dfrac{2\pi}{n})i\)。
单位复根有一些性质:
- \(\omega_n^n=\omega_0^0=1\)
- 对于 \(n=2m\),\(\omega_n^{k}=-\omega_{n}^{k+m}\)
- \(\omega_n^k=\omega_{2n}^{2k}\)
这些奇妙的性质将会在接下来的环节中充分发挥作用。
快速傅里叶变换 / FFT
在 FFT 中,我们将 \(x=\omega_{n}^{k}(0 \leq k \leq n-1)\) 依次 \(f(x)\) 带入求值,便得到了一个 \(n-1\) 次多项式的点值表示法。
但这样不够快,我们考虑分治。
对于 \(n=2^k(k \in \mathbb Z_+)\),设 \(n-1\) 次多项式
设
则有
带入 \(\omega_n^k(0 \leq k < \dfrac n2)\):
带入 \(\omega_n^{k+\frac n2}(0 \leq k < \dfrac n2)\):
因此当我们求出了 \(A(\omega_{\frac n2}^{k}),B(\omega_{\frac n2}^{k})\) 之后,就可以求出 \(A(\omega_{n}^{k}),B(\omega_{n}^{k})\)。该算法的复杂度为 \(T(n)=2T(\dfrac n2)+O(n)=O(n \log n)\)。
但是这样要递归,不够快!于是我们考虑优化。我们如果能求出每个系数最后到了哪个位置,就可以不断地合并这些系数,然后求解。
对于 \(n=8\),我们来看看每次递归之后,系数是怎么被分类的:
把下标用二进制表示
我们观察到,原来在第 \(i\)(从 \(0\) 开始)个位置的系数,最后变到了二进制翻转之后的那个位置。举个例子,\(a_3\) 在现在在第 \(6\) 个位置。\((3)_{10}=(011)_2\),翻转之后就是 \((110)_2=(6)_{10}\)。
记 \(r_i\) 为 \(i\) 二进制翻转之后的值。我们递推求 \(r_i\)。已知 \(r_0=0\)。当 \(i>0\) 时,\(r_{\left \lfloor\frac i2\right \rfloor}\) 已知。我们考虑它在二进制下与 \(r_i\) 的关系:
其中 \(A\) 为 \(n-1\) 位 \(01\) 串,\(B\) 为 \(1\) 位 \(01\) 串,\(+\) 表示连接两个 \(01\) 串。
为什么是 \(A+0\) 呢?观察到 \(\left \lfloor\frac i2\right \rfloor\) 的最高位一定是 \(0\),所以翻转之后的最低位一定是 \(0\)。
同时,观察到 \(B\) 是翻转后的最高位,即 \(i\) 的最低位。
于是,我们得到了 \(r_i(i>0)\) 的递推式:
其中 \(k\) 满足 FFT 的长度 \(n=2^k\)。
这个操作叫做蝴蝶变换,也称位逆序变换。
inline void change(Poly &f,int len){
for(int i=0;i<=len;++i){
rev[i]=(rev[i>>1]>>1);
if(i&1){
rev[i]|=(len>>1);
}
}
for(int i=0;i<=len;++i){ // 保证每一个对只会被翻转一次
if(i<rev[i]){
std::swap(f[i],f[rev[i]]); // 直接将系数扔到最后的位置 然后 FFT
}
}
return;
}
点值相乘
在求出多项式 \(f,g\) 的 \(n\) 组点值后,我们要求 \(h=f\times g\) 的 \(n\) 组点值。显然,\(f(i)g(i)=h(i)\)。于是我们对求出点值进行对位相乘的操作,就得到 \(h\) 的 \(n\) 组点值。
下文中,我们会讲解如何通过带入的 \(n\) 组特殊点值还原出多项式本身。容易发现,对 \(h\) 进行这个过程,还原出的多项式就是 \(f\times g\)。
快速傅里叶逆变换 / IFFT
我们通过 FFT 求出了 \(n\) 组点值。记它们为 \(y_0,y_1,\cdots,y_{n-1}\),其中 \(y_i=f(\omega_n^i)\)。
设多项式
则取 \(x=\omega_n^{-i}(0 \leq i \leq n-1)\) 对 \(A\) 进行 FFT,得到的点值序列就是原来 \(a\) 序列的 \(n\) 倍。
接下来来证明一下:
后面的和式在 \(\omega_n^{j-k}=1\) 时值为 \(n\),此时 \(n \mid (j-k)\),由这两个和式的范围可得 \(j=k\)。
在 \(\omega_n^{j-k} \neq 1\)(此时 \(j \neq k\))时,\(\sum \limits_{i=0}^{n-1} {(\omega_n^{j-k})}^{i}\) 是一个等比数列求和
由单位复根的性质得该式值为 \(0\)。
则我们继续推导,
于是我们只需要在 FFT 时将单位根变为 \(\omega_n^{-1}\),再进行 FFT,就完成了 IFFT。
# include <bits/stdc++.h>
const int N=4000010;
struct Complex{
double x,y;
Complex(double _x=0.0,double _y=0.0){
x=_x,y=_y;
return;
}
Complex operator + (const Complex &b) const{
return Complex(x+b.x,y+b.y);
}
Complex operator - (const Complex &b) const{
return Complex(x-b.x,y-b.y);
}
Complex operator * (const Complex &b) const{
return Complex(x*b.x-y*b.y,x*b.y+y*b.x);
}
};
typedef std::vector <Complex> Poly;
const double PI=acos(-1.0);
int rev[N];
Poly F,G;
int n,m;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-')f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
inline void change(Poly &f,int len){ // 蝴蝶变换
for(int i=0;i<=len;++i){
rev[i]=(rev[i>>1]>>1);
if(i&1){
rev[i]|=(len>>1);
}
}
for(int i=0;i<=len;++i){
if(i<rev[i]){
std::swap(f[i],f[rev[i]]);
}
}
return;
}
inline void fft(Poly &f,int len,double op){
change(f,len);
for(int h=2;h<=len;h<<=1){
Complex wn(cos(2*PI/h),sin(op*2*PI/h));
for(int j=0;j<len;j+=h){
Complex w(1,0);
for(int k=j;k<j+h/2;++k){
Complex u=f[k],t=w*f[k+h/2];
f[k]=u+t,f[k+h/2]=u-t;
w=w*wn;
}
}
}
return;
}
int main(void){
n=read(),m=read();
int maxlen=1;
while(maxlen<=n+m){ // 注意是 <= 而非 <
maxlen<<=1;
}
F.resize(maxlen+5),G.resize(maxlen+5);
for(int i=0;i<=n;++i){
F[i]=Complex(read(),0);
}
for(int i=0;i<=m;++i){
G[i]=Complex(read(),0);
}
fft(F,maxlen,1),fft(G,maxlen,1);
for(int i=0;i<=maxlen;++i){
F[i]=F[i]*G[i];
}
fft(F,maxlen,-1);
for(int i=0;i<=n+m;++i){
printf("%d ",(int)(F[i].x/maxlen+0.5));
}
return 0;
}


